Eine Ortskurve bzw. ein Trägergraph ist eine Kurve, auf der Punkte einer Funktionenschar liegen, die eine bestimmte Gemeinsamkeit bzw. Eigenschaft haben.
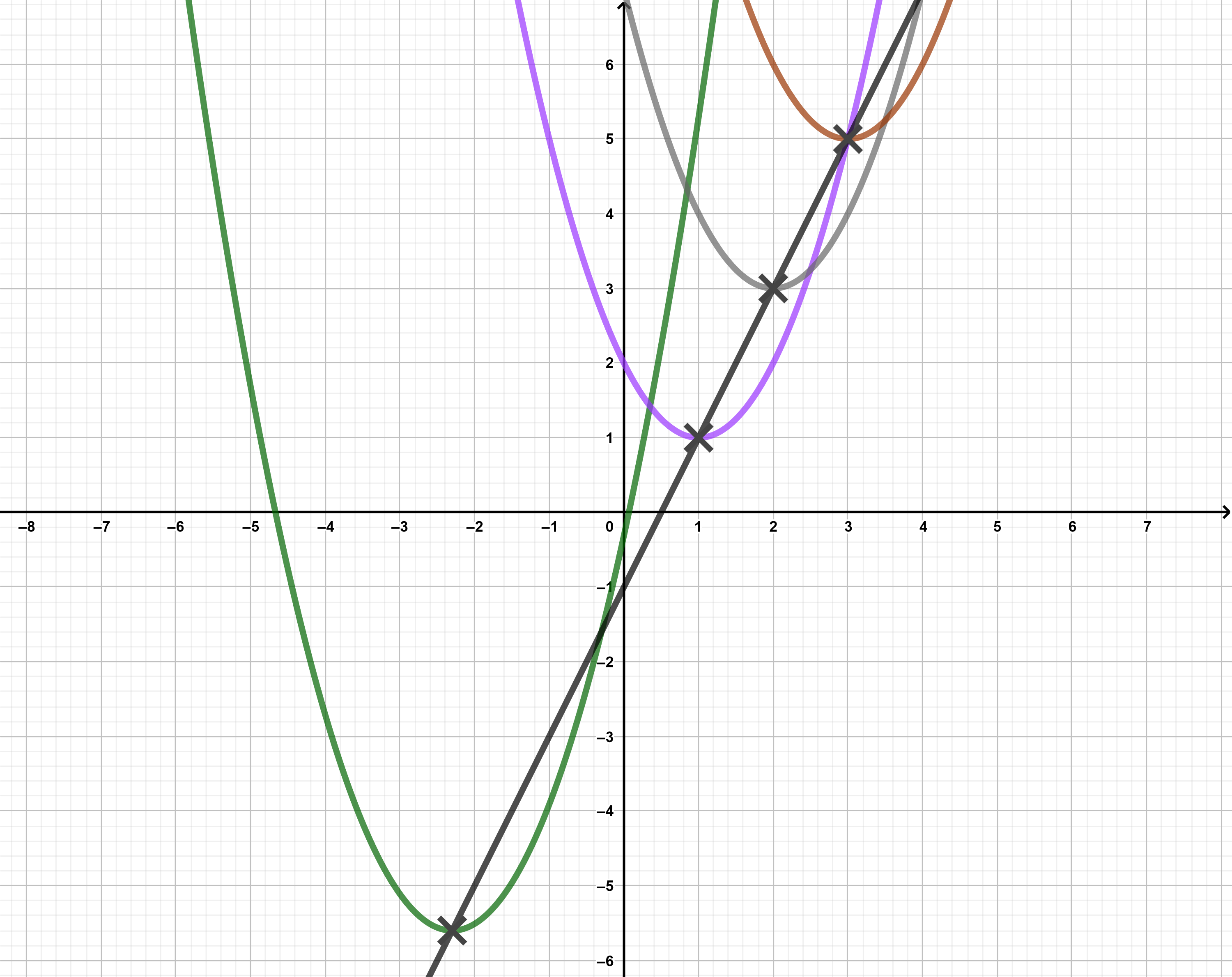
Die Gemeinsamkeit könnte sein, dass alle Punkte Extrempunkte (z.B. Scheitelpunkte von Parabeln) oder Wendepunkte der Funktionenschar sind. Eine Ortskurve könnte beispielsweise eine Kurve durch die Scheitelpunkte einer Parabelschar sein.
Eine weitere häufige Gemeinsamkeit kann sein, dass alle Punkte auf einer Geraden liegen, die sich durch Drehung oder Spiegelung von Geraden oder Punktescharen an Ursprungsgeraden ergibt.
Veranschaulichung durch Applets
Das folgende Applet beschreibt die Funktionenschar . Verschiebt man den Schieberegler für , so sieht man, dass sich der Scheitelpunkt auf der eingezeichneten Geraden bewegt.
In zweiten Applet sieht man die Funktionenschar . Wenn man den Schieberegler für den Wert von verschiebt, wird der Scheitelpunkt eingezeichnet. Man erkennt, dass die Scheitelpunkte eine Parabel beschreiben.
In diesem dritten Applet kann der Punkt beliebig auf der Geraden verschoben werden. Punkt ist auch frei. Die anderen beiden Punkte passen sich so an, dass sich ein Quadrat ergibt. Die Gerade ist der Trägergraph für den Punkt .
Allgemeine Vorgehensweise
Beispiel:
Finde die Ortskurve der Scheitelpunkte der Funktionenschar .
Allgemein | Beispiel |
|---|---|
1) Man bestimme die gesuchten Punkte (Scheitelpunkte, Extrema, Wendepunkte) in Abhängigkeit des Parameters. | Man lese den Scheitelpunkt aus der Scheitelpunktsform ab: |
2) Man stelle den Zusammenhang zwischen dem Parameter und der x-Komponente bzw. dem Parameter und der y-Komponente jeweils in einer Gleichung dar. |
|
3) Man hat nun zwei Gleichungen gefunden. Die erste Gleichung löst man nach dem Parameter auf und setzt diese in die zweite Gleichung. | 1.Gleichung nach aufgelöst und in die 2. Gleichung eingesetzt |
4) Dadurch erhält man die Gleichung für die gesuchte Ortskurve. | Ortskurve: |
Beispielaufgaben
Ortskurve der Scheitelpunkte bei Parabeln
Beschreibung | Beispiel |
|---|---|
Bilde die Scheitelform mithilfe der quadratischen Ergänzung. | |
Lies aus dieser Darstellung den Scheitelpunkt ab. | Scheitelpunkt: |
(1. Gleichung) | |
(2. Gleichung) | |
Setze die 1. Gleichung in die 2. Gleichung ein. | |
Vereinfache. |
Funktionsgleichung für Ortskurve:
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Bestimmung von Ortskurven
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
