Viele Polynome kannst du als Produkt der Form darstellen. Hierbei sind bis die Nullstellen der Funktion und .
Diese Darstellung heißt Linearfaktordarstellung.
, ,..., heißen Linearfaktoren.
Bringt man ein Polynom in seine Linearfaktordarstellung, so nennt man diesen Vorgang Linearfaktorzerlegung.
Beispiel:
kann umgeformt werden zu
Die Funktion hat die Nullstellen und .
Für Polynome, bei denen eine solche Darstellung nicht möglich ist, gibt es eine Darstellung, die der Linearfaktordarstellung ähnlich ist:
Das Restglied ist wieder ein Polynom, welches keine reellen Nullstellen hat und daher nicht weiter zerlegt werden kann.
Beispiel:
kannst du zerlegen in
hat in den reellen Zahlen keine Nullstellen, da
nicht weiter lösbar ist.
Bestimmung der Linearfaktordarstellung
Geschicktes Umformen
Versuche als erstes, ob du durch geschicktes Ausklammern und/oder Einsatz der binomischen Formeln dein gegebenes Polynom in eine Linearfaktordarstellung bringen kannst.
Beispiel:
Durch Umformen erhältst du:
| ↓ | Klammere aus. | ||
| ↓ | ist eine binomische Formel. Schreibe diese um. | ||
Die Linearfaktordarstellung ist also
Nullstellenbestimmung
Wenn du mit geschicktem Umformen nicht weiterkommst, bestimme alle Nullstellen.
Nutze bei quadratischen Funktionen die Mitternachtsformel oder pq-Formel.
Rate Nullstellen bei Polynomen vom Grad größer , um eine Polynomdivision durchzuführen.
Bilde ein Produkt aus den Linearfaktoren der Nullstellen und überprüfe, ob dieses Produkt deiner Funktion entspricht. Passe, wenn nötig, die Linearfaktordarstellung ein wenig an.
Gegebenenfalls kommen manchen Linearfaktoren mehrfach vor, je nach Vielfachheit der Nullstelle.
Füge, wenn nötig, einen geeigneten Faktor hinzu.
Beispiel:
Berechne mit der Mitternachtsformel oder der pq-Formel alle Nullstellen der Funktion. Mit der Mitternachtsformel ergeben sich folgende Nullstellen und :
und
enthält in der Linearfaktorzerlegung also die Linearfaktoren und . Teste, ob ist:
Probe:
unterscheidet sich nur um den Faktor von . Multipliziere mit , um die Linearfaktordarstellung von zu erhalten:
hat also die Linearfaktordarstellung .
Linearfaktordarstellung in Abhängigkeit der Nullstellen
Im Allgemeinen hat ein Polynom n-ten Grades die Form
und besitzt maximal Nullstellen.
Es lassen sich nun 2 Fälle unterscheiden:
Entweder das Polynom hat Nullstellen, wenn man mehrfache Nullstellen dabei auch mehrfach zählt, (es müssen also nicht verschiedene Nullstellen sein)
oder das Polynom hat trotz Zählung aller Nullstellen mit ihren Vielfachheiten immer noch weniger als Nullstellen.
Beispiele
Polynom n-ten Grades hat Nullstellen:
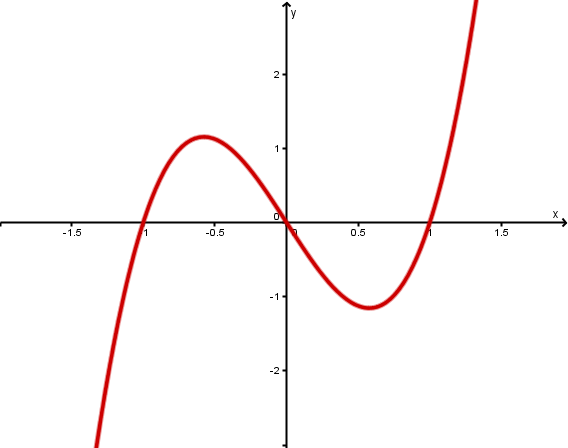
Das Polynom von oben hat den Grad und zwei Nullstellen, und zwar und .
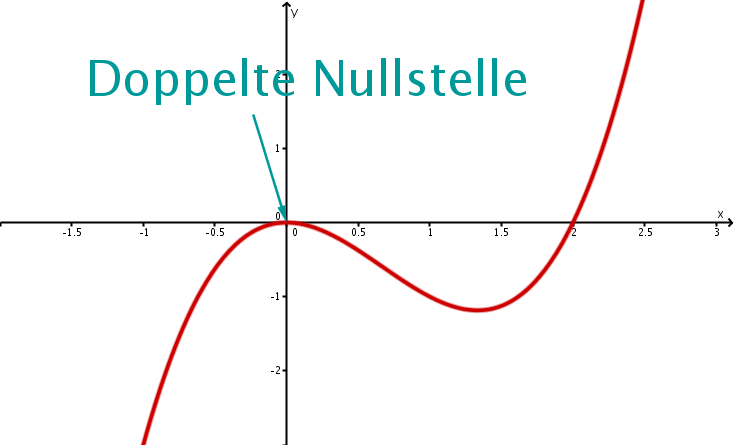
Das Polynom hat den Grad und eine doppelte Nullstelle, und zwar die Zahl .
Polynom n-ten Grades hat weniger als Nullstellen:
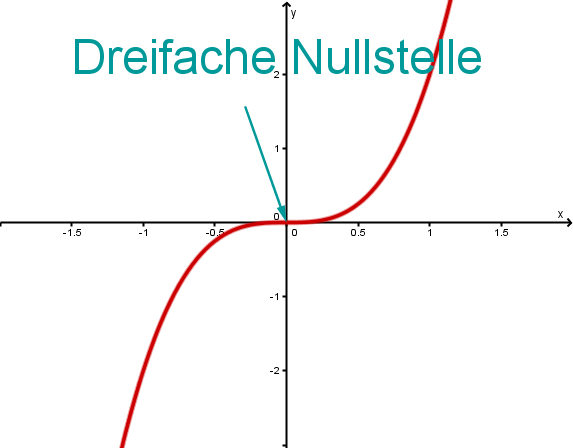
Das Polynom von oben hat den Grad 3 und nur eine Nullstelle, und zwar die Zahl .
Nullstellen
Wenn ein Polynom n-ten Grades mit Nullstellen ist und mehrfache Nullstellen auch mehrfach gezählt werden, dann gibt es eine Linearfaktorzerlegung von . lässt sich also umformen zu
mit als Nullstellen des Polynoms (wobei auch mehrere Nullstellen gleich sein können).
Beispiele
1.
Linearfaktordarstellung:
2.
Linearfaktordarstellung:
3.
Linearfaktordarstellung:
Weniger als Nullstellen
Im Allgemeinen kann man über den reellen Zahlen aber nicht davon ausgehen, dass ein Polynom seinem Grad entsprechend viele Nullstellen besitzt (z. B. besitzt überhaupt keine Nullstellen, hat aber Grad 2).
Für solche Polynome gibt es eine Darstellung, die der Linearfaktordarstellung ähnlich ist:
wobei das wieder ein Polynom ist, welches allerdings keine reellen Nullstellen besitzt.
Das Restglied lässt sich zum Beispiel mithilfe der Polynomdivision berechnen, indem man das Ausgangspolynom durch die zu seinen Nullstellen gehörenden Linearfaktoren teilt.
Beispiel

Außerdem lässt sich das Restglied selbst als Produkt von Polynomen vom Grad 2 schreiben.
Vorteile der Linearfaktordarstellung
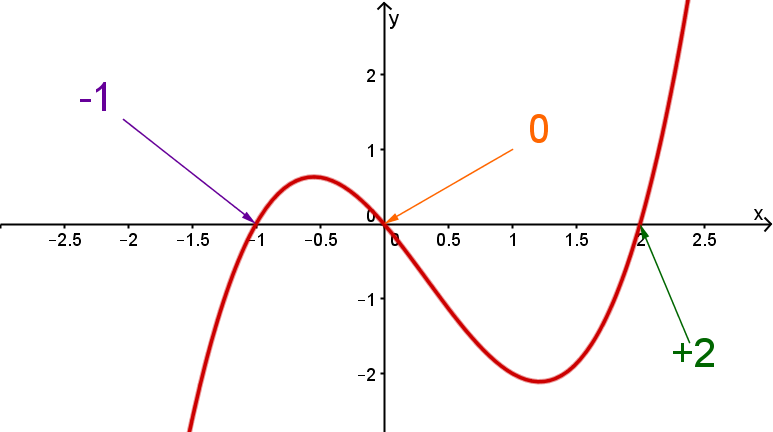
Ablesen der Nullstellen des Polynoms
Liegt ein Polynom in Linearfaktordarstellung vor, so kann man an ihm ohne weitere Rechnung die Nullstellen und ihre Vielfachheiten ablesen, da in jedem Linearfaktor eine Nullstelle steht.
Beispiel
Vereinfachen von Bruchtermen
Die Linearfaktorzerlegung ist eine wichtige Technik im Umgang mit Bruchtermen.
1) Die Linearfaktorzerlegung verwandelt eine Summe oder Differenz in ein Produkt. Nur aus Produkten heraus kann man kürzen, nicht aus Differenzen oder Summen. Das Kürzen vereinfacht den Term oft erheblich.
Beispiel
2) Will man den Hauptnenner zweier oder mehrerer Bruchterme bestimmen, muss man zunächst die Nenner der Brüche faktorisieren. Dazu benötigt man ihre Linearfaktordarstellung.
Beispiel
soll zusammengefasst werden. Mithilfe der Linearfaktordarstellung erkennt man den Hauptnenner und kann die Terme gleichnamig machen:
3) Durch Kürzen des Funktionsterms kann man bei gebrochenrationalen Funktionen gegebenenfalls die stetige Fortsetzung ermitteln.
Beispiel
ergibt, dass
die stetige Fortsetzung von ist.
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Linearfaktorzerlegung
