Die Logarithmusfunktion mit der Basis , der Eulerschen Zahl, wird natürlicher Logarithmus oder auch -Funktion genannt. Ihre Funktionsvorschrift ist:
Dabei bezeichnet den Logarithmus zur Basis , also .
Eigenschaften
Die -Funktion hat die gleichen Eigenschaften wie Logarithmusfunktionen zu beliebigen Basen. Weil ist sie monoton steigend.
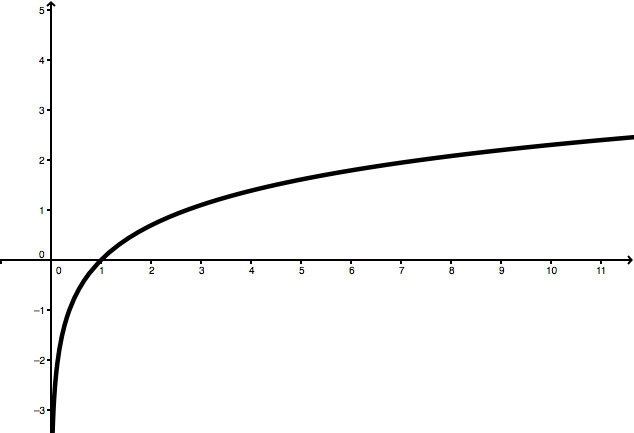
Graph der -Funktion:

Beziehung zu anderen Funktionen
Umkehrfunktion
Die Umkehrfunktion der -Funktion ist die -Funktion. Für gilt also:
Ableitung
Die Ableitung von , ist gegeben durch:
Stammfunktion
Das erste Integral bzw. eine Stammfunktion zu lautet:
Zur Herleitung bzw. Berechnung der Stammfunktion siehe den Artikel Partielle Integration.
Beliebige Logarithmusfunktion als ln-Funktion
Einen Logarithmus zu einer beliebigen Basis (mit , ), kannst du über folgende Formel in eine ln-Funktion überführen:
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Gemischte Aufgaben zur e- und ln-Funktion
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
