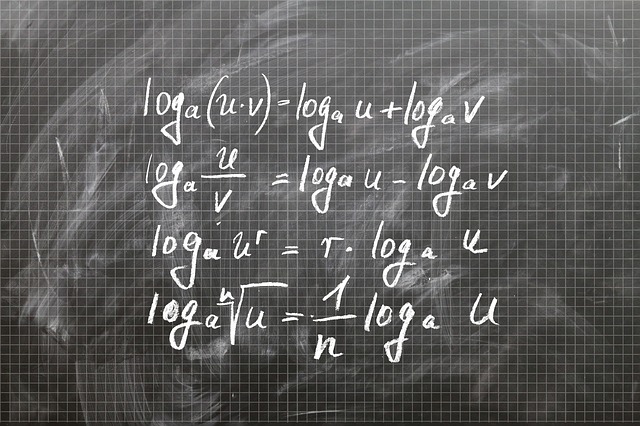Definition des Logarithmus
Mit bezeichnet man die eindeutige Lösung der Gleichung . Dabei nehmen wir an, dass und positive Zahlen sind. Das heißt, es gilt:
So ist , weil ist.
Rechenregeln
Produkt zu Summe | Quotient zu Differenz | Potenz zu Produkt | |
|---|---|---|---|
Spezialfälle (ergeben sich aus den Rechenregeln) |
Beispiel
Gegeben ist ein Term, der möglichst weit vereinfacht werden soll: | |||
| ↓ | |||
| ↓ | Hier kann man die "Quotienten- und Produktregel" für Logarithmen anwenden. | ||
| ↓ | Dann vereinfacht man den ersten Summanden mit der Potenz-zu-Produkt-Regel und löst die Minusklammer auf. | ||
| ↓ | Die Logarithmen mit Argument kann man nun zusammenfassen und die Logarithmen mit Zahlen als Argument berechnen. Dazu formt man die Argumente zunächst in Dreierpotenzen um. | ||
| ↓ | Nun kann man mit der Potenz-zu-Produkt-Regel lösen und die Zahlenwerte zusammenfassen. | ||
Basisumrechnung
Kennt man den Logarithmus zu einer bestimmten Basis , so kann man damit den Logarithmus zu einer beliebigen Basis mit folgender Formel berechnen:
Somit kann man beispielsweise Logarithmen zu einer beliebigen Basis mit dem Taschenrechner berechnen, auch, wenn dieser nur den natürlichen Logarithmus oder den Zehnerlogarithmus (also zur Basis 10) bereitstellt.
Beispiele
16 und 64 sind Potenzen von 4. Daher formt man den Ausdruck links geschickt zur Basis 4 um | |||
| ↓ | |||
| ↓ | Man schreibt und als Viererpotenzen und löst dann mit der Potenz-zu-Produkt-Regel | ||
Eine ähnliche Methode zur genauen Berechnung eines Logarithmusausdrucks nennt sich Exponentenvergleich:
Schreibe den Logarithmusausdruck in die Form zurück, aus der er entstanden ist. Der Logarithmus fragt nach: " hoch was ergibt ?"
Erkenne hier, dass und beides Zahlen sind, die auch durch eine Zweierpotenz darstellbar sind.
Mit den Potenzgesetzen kann der Ausdruck umgeformt werden.
Der Exponentenvergleich erlaubt es, bei Gleichungen, bei denen auf beiden Seiten ein Exponentialausdruck mit gleicher Basis steht, nur die Exponenten in die Gleichung zu schreiben.
Die Gleichung ist nun sehr leicht ohne Taschenrechner zu lösen. Das Ergebnis ist die vereinfachte Form des Logarithmusausdrucks.
Berechnung von nur mit dem natürlichen Logarithmus:
Die rechte Seite kann man nun leicht mit einem Taschenrechner berechnen, der nur den natürlichen Logarithmus bereitstellt.
Anwendung
Mit dem Logarithmus lassen sich Exponentialgleichungen lösen. Auch bestimmte Stellen von Exponentialfunktionen werden mithilfe des Logarithmus gefunden.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: