Aufgaben zu Rotationskörpern
Schaffst du es, Volumen und Oberflächen von Rotationskörpern zu berechnen? Teste dich mit diesen gemischten Aufgaben!
- 1
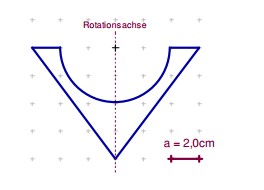
Ein rotationssymmetrisches Werkstück soll aus Gusseisen der Dichte hergestellt werden.
Das Bild zeigt das Werkstück im Querschnitt. Berechne die Masse des Werkstücks.
- 2
Die nebenstehende Figur rotiert um die Achse A.
Berechne das Volumen des Rotationskörpers in Abhängigkeit von a.

- 3
Berechne in Abhängigkeit von Volumen und Oberfläche des Rotationskörpers, der durch Rotation der Figur um die Achse entsteht.
Wie groß muss sein, damit das Volumen 1 Liter beträgt?

- 4
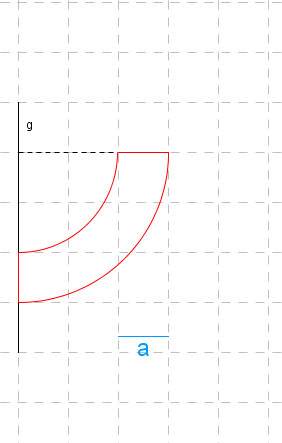
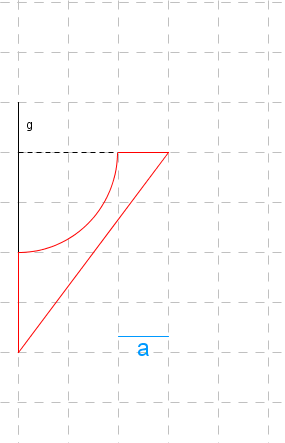
Durch Rotation des dargestellten rot umrandeten Flächenstücks um die Achse entsteht ein rotationssymmetrischer Körper. Bestimme jeweils das Volumen und den Oberflächeninhalt dieses Rotationskörpers in den Einheiten bzw. .
- 5
Zeichne einen Axialschnitt für den Rotationskörper.
Maße: ;
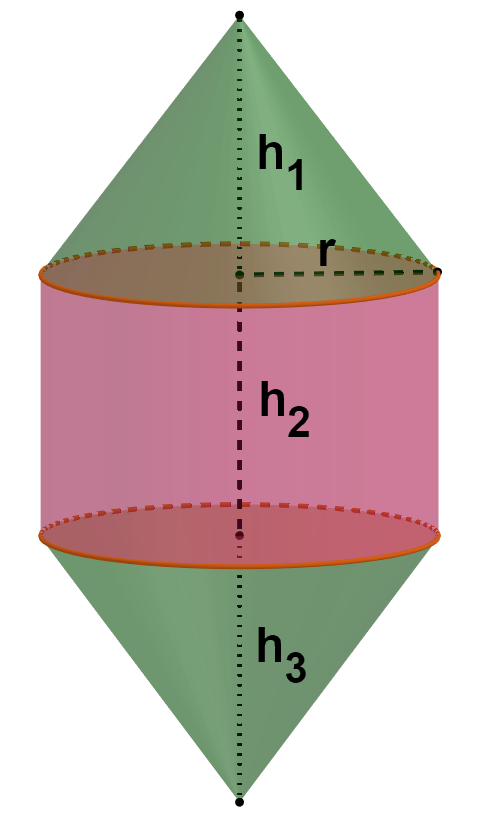
- 6
Die abgebildeten Figuren rotieren um die eingezeichnete Achse . Beschreibe den Rotationskörper der dann entsteht.
Maße:
Kreisradius
Basis des Dreiecks
Höhe des Dreiecks
Maße:
entsprechend der Zeichnung
- 7
Gegeben ist ein Rotationskörper. Welches Bild stellt seinen Axialschnitt dar?
- 8
Gegeben ist ein Rotationskörper. Welches Bild stellt seinen Axialschnitt dar?
- 9
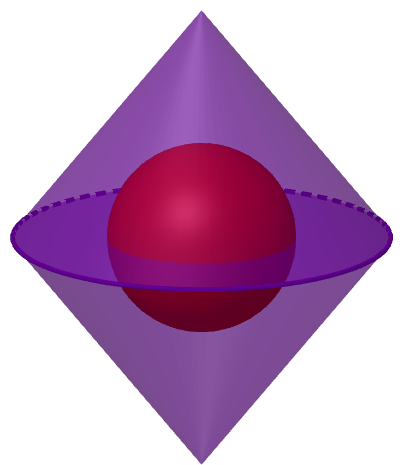
Gegeben ist ein Rotationskörper.
Zeichne seinen Axialschnitt.
Maße:
Kugelradius: ,
Kegelradius: ,
Kegelhöhe:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
























