Aufgaben zum Volumen eines Prisma
Teste dein Wissen zu Prismen mit diesen gemischten Übungsaufgaben! Lerne, das Volumen von beliebigen Prismen zu bestimmen.
- 1
Welches Volumen hat ein hohes Haus mit der Breite und der Länge , wenn das Dachgeschoss hoch ist?

Quelle: torange.biz, CC-BY-SA-4.0
- 2
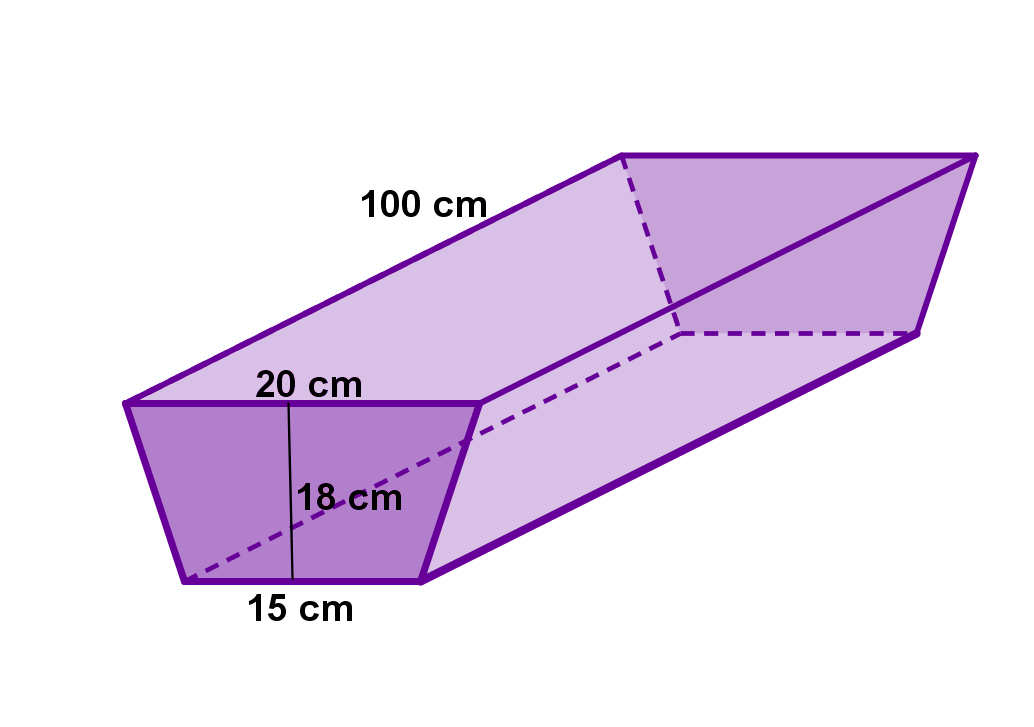
Filmon hat einen Blumenkasten. Der Blumenkasten hat 100 cm Länge und 18 cm Höhe. Unten ist er 15 cm breit und oben 20 cm. Wie groß ist das Volumen des Blumenkastens?
 cm³
cm³ - 3
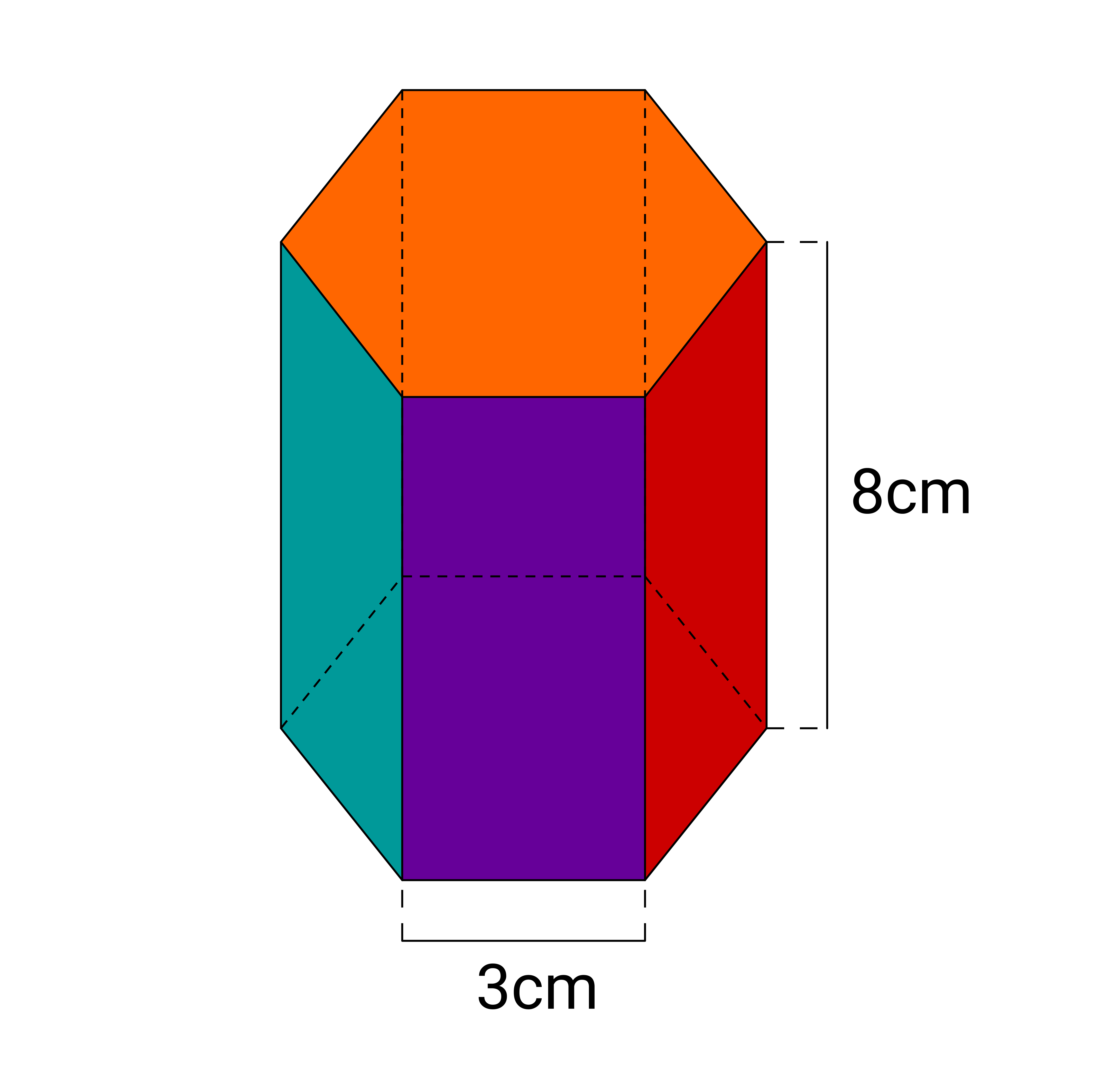
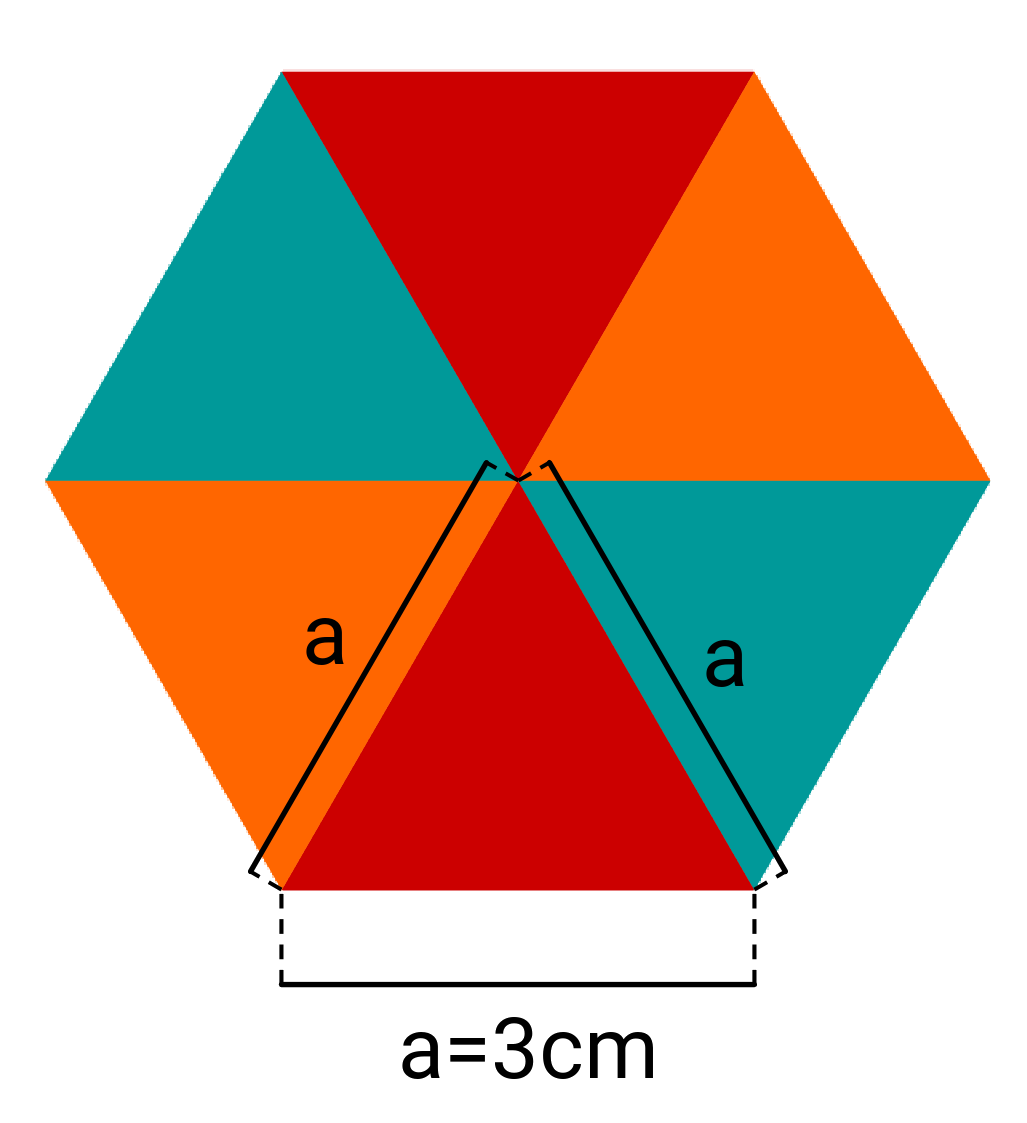
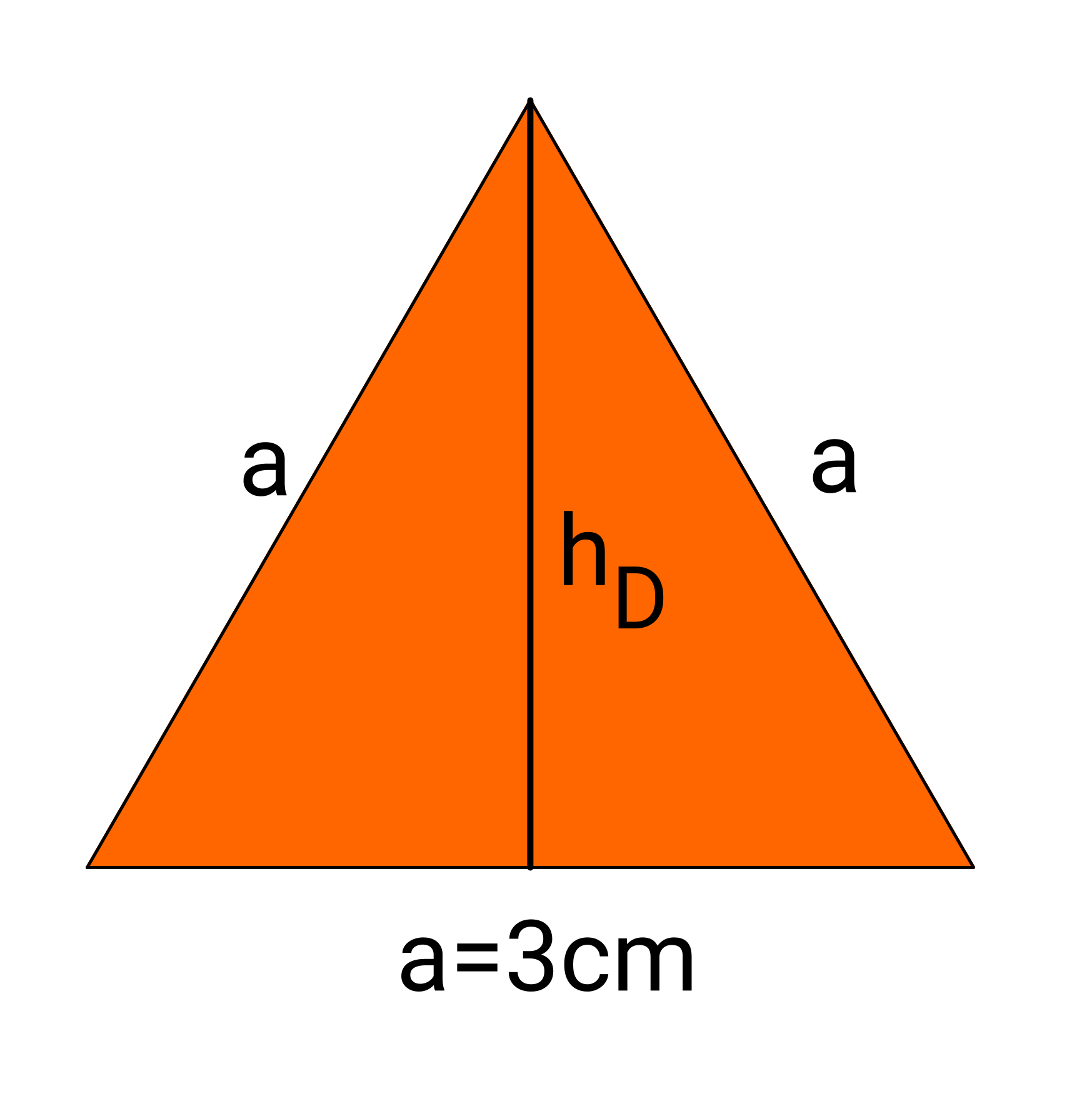
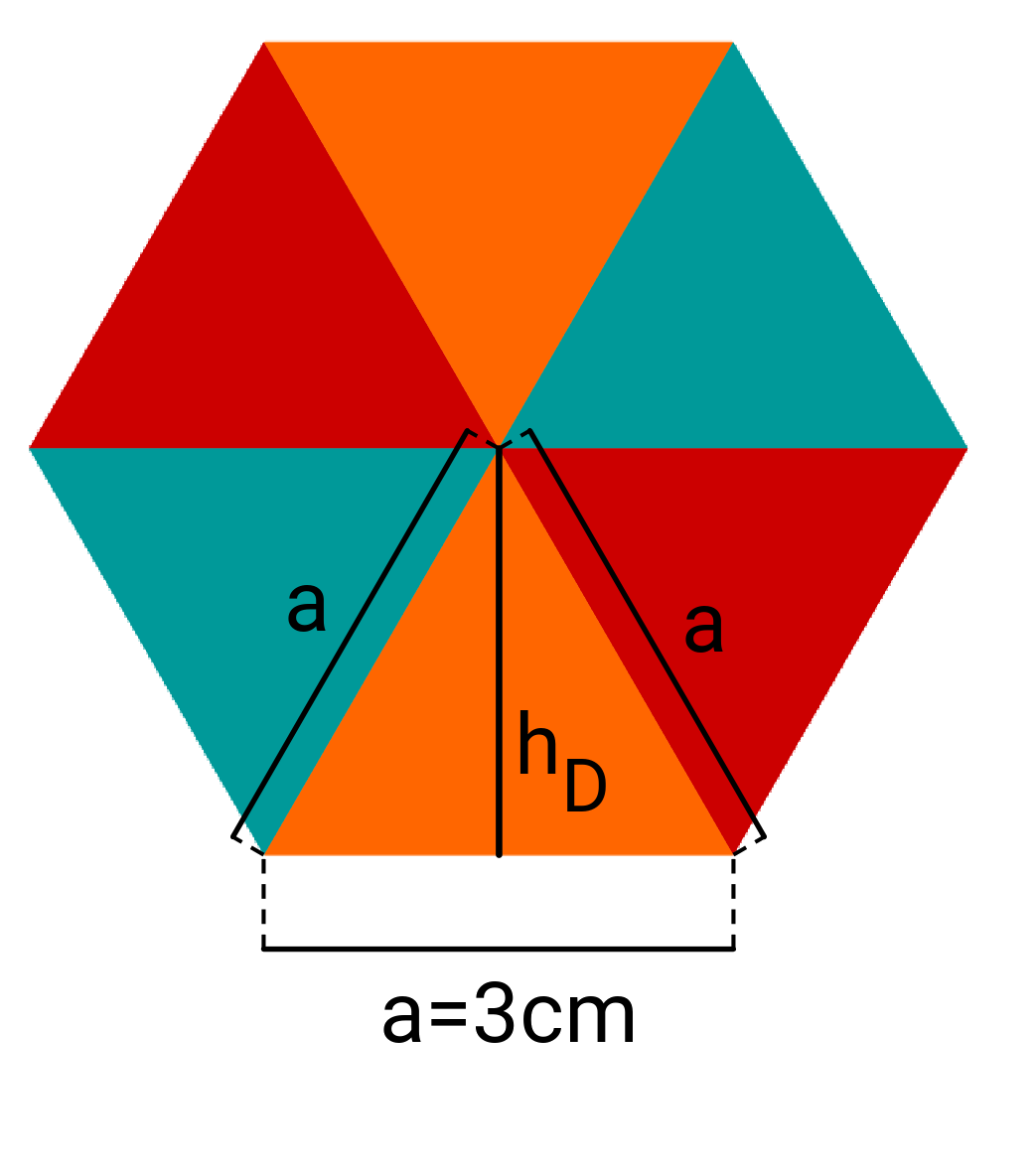
Ein Marmeladenglas hat als Grundfläche ein regelmäßiges Sechseck und ist (abgesehen vom Rand mit Schraubverschluss und Deckel) hoch. Die Seitenlänge des Sechseckes ist .
Wie viel Milliliter Marmelade passen in das Glas, wenn man es bis unter den Rand füllt?
 ml
ml
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?