Aufgaben zur Kugel
Hier findest du gemischte Aufgaben zum Thema Kugel. Lerne in diesen Aufgaben, die Oberfläche und das Volumen einer Kugel zu berechnen.
- 1
Berechne mit den gegebenen Informationen das Volumen der Kugel.
Radius
Radius
Durchmesser
Umfang
Oberfläche
- 2
Berechne mit den gegebenen Informationen die Oberfläche der Kugel.
Radius 1cm
Radius 5cm
Durchmesser 3cm
Volumen
Umfang 7cm
- 3
Berechne mit den gegebenen Informationen den Umfang der Kugel.
Radius
Durchmesser
Oberfläche
Volumen
- 4
Der Durchmesser einer Murmel ist . Wie groß ist ihr Volumen? Runde auf ganze .
 mm³
mm³ - 5
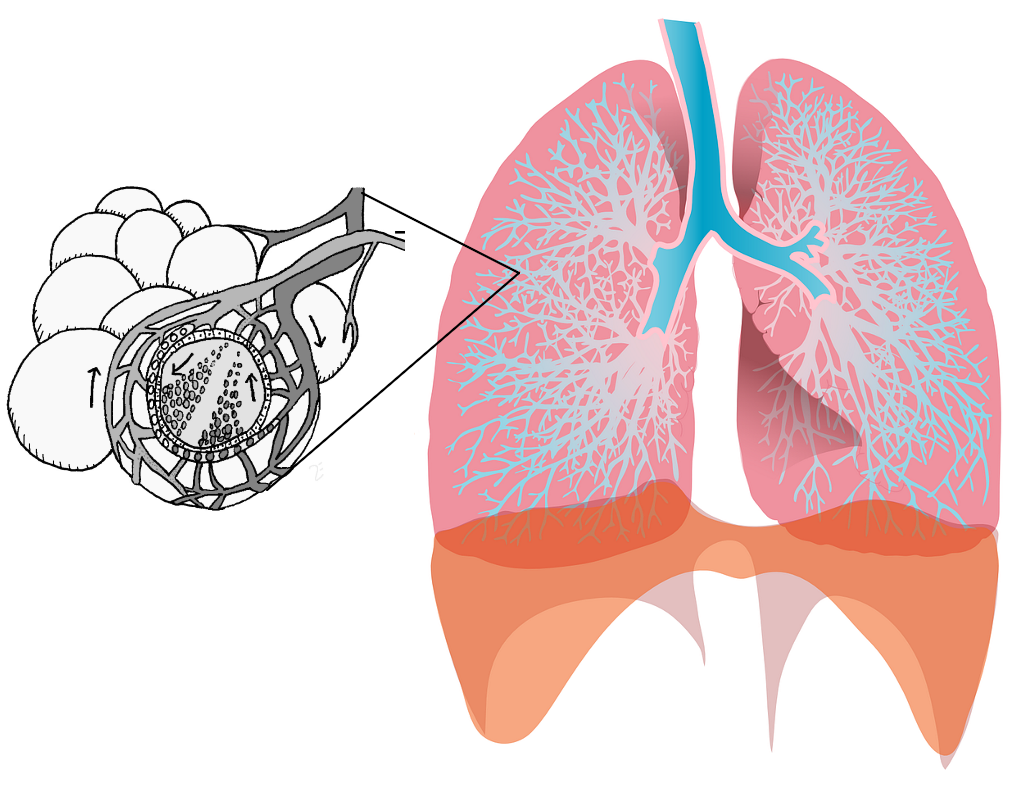
Die menschliche Lunge besteht aus annähernd kugelförmigen Lungenbläschen. In einer Lunge finden sich ca. ( ) Bläschen. Über die Oberfläche dieser Bläschen nimmt der menschliche Organismus Sauerstoff aus der Luft auf. Wenn wir ausatmen, hat ein Lungenbläschen einen Durchmesser von . Wenn wir einatmen, blähen sie sich auf und erreichen einen Durchmesser von .
Berechne die Oberfläche und das Volumen eines einzelnen Lungenbläschens beim Aus- und beim Einatmen.
Berechne das Volumen und die Oberfläche aller Bläschen zusammen beim Aus- und Einatmen.
Wie groß müsste der Radius einer einzelnen Kugel sein, die dasselbe Volumen hat wie alle Bläschen zusammen? Unterscheide dabei wieder das Ein- und Ausatmen! Wie groß ist die Oberfläche dieser Kugel?
Wie groß müsste der Radius einer einzelnen Kugel sein, die dieselbe Oberfläche hat wie alle Bläschen zusammen? Unterscheide dabei wieder das Ein- und Ausatmen!
Zusatzaufgabe: Was ist der Vorteil von vielen kleinen Bläschen anstelle einer großen Kugel als Lunge?
- 6
Eine Bestellung für Eisenkugeln liegt vor. Jede Kugel soll einen Durchmesser von haben. Wieviel Eisen braucht der Hersteller? Und könntest du das Eisenstück heben, woraus die Kugeln gegossen werden, wenn du heben kannst? (Dichte von Eisen: ). Runde auf zwei Nachkommastellen.
- 7
Nach einem Hagelschauer hat Herr Sammler jede Menge Hagelkörner aufgesammelt. Alle sind nahezu kugelförmig und haben einen durchschnittlichen Durchmesser von . Herr Sammler hat insgesamt 47 Hagelkörner aufgesammelt. Wenn alle Hagelkörner schmelzen würden, könnte er das Wasser in nur einem 2 Liter Eimer aufbewahren? ( = )
- 8
Sandra ist mit ihren Freundinnen am Strand, und sie möchten mit dem Wasserball spielen.
Wie viel Liter Luft muss Sandra in den Ball blasen, damit er einen Durchmesser von hat?
Runde auf ganze .
 cm³
cm³
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?