Aufgaben zur Berechnung des Volumens zusammengesetzter Körper
Wie gut kennst du dich mit zusammengesetzten Körpern aus? Lerne mit diesen Aufgaben, das Volumen zu bestimmen mithilfe verschiedener Strategien!
- 1
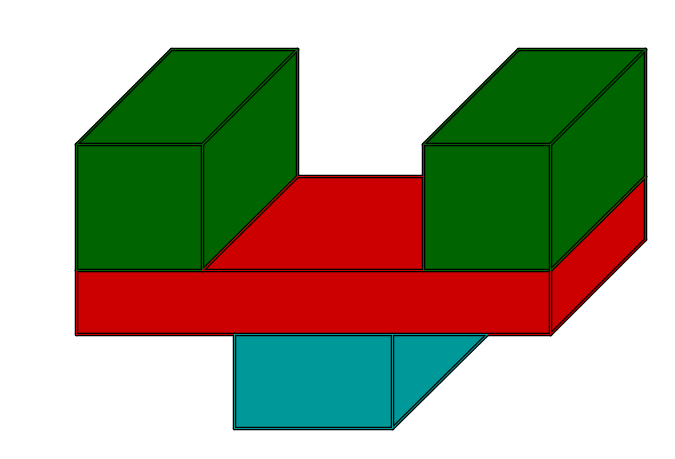
Berechne durch geschicktes Aufteilen das Volumen des gegebenen Körpers.

- 2
Berechne durch geschicktes Aufteilen das Volumen des gegebenen Körpers. Gib das Ergebnis auf eine Stelle nach dem Komma gerundet OHNE Größeneinheit an!

- 3
Berechne das Volumen des folgenden Körpers durch geschicktes Aufteilen in Quader.
- 4
Welches Volumen hat ein hohes Haus mit der Breite und der Länge , wenn das Dachgeschoss hoch ist?

Quelle: torange.biz, CC-BY-SA-4.0
- 5
In Nîmes in Frankreich steht einer der am besten erhaltenen römischen Tempel, die Maison Carrée. Berechne das Volumen des Tempels mit den zehn breiten Säulen mithilfe des Modells.

- 6
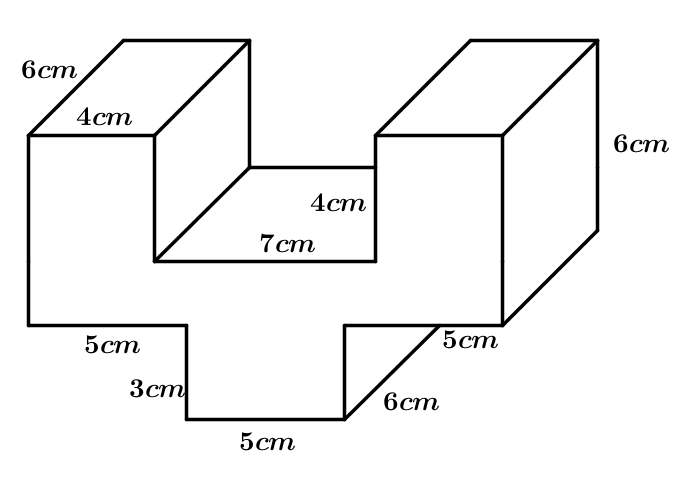
Berechne das Volumen des E-förmigen Körpers

- 7
Sina mag ihre Apfelschorle schön kalt und möchte daher so viele Eiswürfel wie möglich in ihrem Glas. Im Glas passen . Die Eiswürfel sind alle Würfel der Kantenlänge . In dem Glas befinden sich genau Apfelschorle.
Wie viele Eiswürfel passen höchstens in das Glas, ohne dass die Apfelschorle überläuft?
Nimm dafür an, dass das gesamte Volumen der eingeschenkten Eiswürfel "Unterwasser" liegt.
 Eiswürfel
Eiswürfel - 8
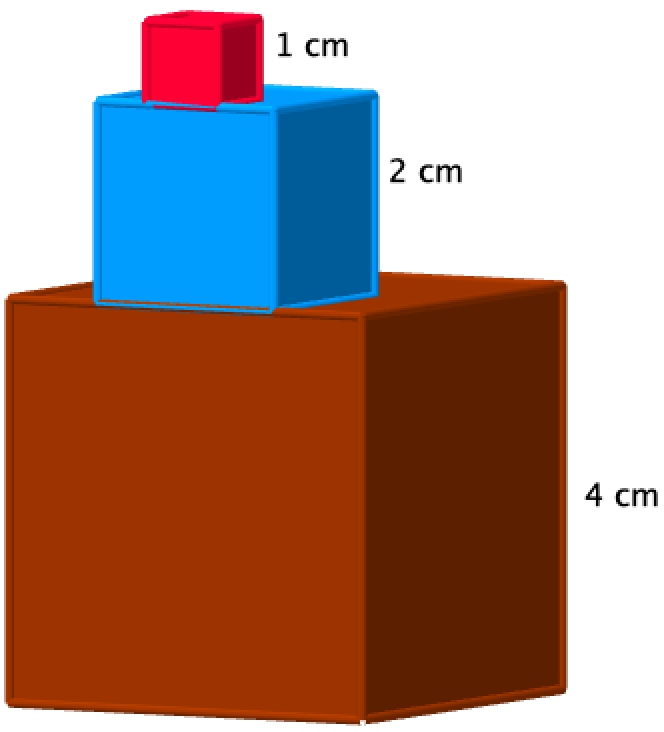
In der nebenstehenden Skizze wurde aus würfelförmigen Bauklötzen ein Turm gebaut. Berechne das Volumen des Turms.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?