Der Erwartungswert ist ein Wert in der Stochastik und kommt im Zusammenhang mit Zufallsgrößen vor. Man kann sagen, der Erwartungswert festigt sich als Mittelwert der Ergebnisse bei mehrmaligem Wiederholen eines Experiments.
Der Erwartungswert sollte nicht mit dem arithmetischen Mittel verwechselt werden, hängt aber mit ihm zusammen.
Zum Beispiel erwartet man beim 6-maligen Werfen eines fairen Würfels einmal die Zahl "5" und durchschnittlich die Augenzahl 3,5. Wenn man den Würfel 6-mal wirft, kann die Zahl "5" jedoch 0- bis 6-mal auftreten und die durchschnittliche Augenzahl im Intervall von 1 bis 6 liegen.
Berechnung
Formel
Für eine diskrete Zufallsgröße mit Werten und deren Wahrscheinlichkeiten berechnet man den Erwartungswert, den man normalerweise mit oder bezeichnet, wie folgt.
Der Erwartungswert berechnet sich also als Summe der Produkte von Wert und dessen Wahrscheinlichkeit.
Beispiel
Werfen von zwei Laplace-Würfeln. Die Werte der Zufallsgröße sind genau die Summe der Augenzahlen.
Damit ergibt sich für den Erwartungswert für dieses Experiment.
Dies bedeutet also, dass man beim Werfen von zwei fairen Würfeln im Mittel eine "7" würfelt.
Formel
Für eine stetige Zufallsvariable mit Werten in und Dichtefunktion berechnet man den Erwartungswert, den man auch hier mit oder bezeichnet, wie folgt.
Der Erwartungswert berechnet sich also als Integral über das Produkt der Ergebnisse und der Dichtefunktion der Verteilung.
Beispiel
Die Verspätung einer U-Bahn sei mit folgender Dichtefunktion ( ist die Minute, in der die U-Bahn eintrifft) gegeben
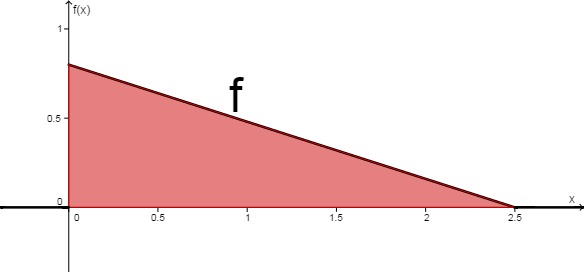
Daraus ergibt sich für den Erwartungswert dieses Experimentes
Das bedeutet, die U-Bahn hat im Schnitt Minuten, das sind Sekunden, Verspätung.
Rechenregeln
Erwartungswert von Summen von Zufallsvariablen. X und Y sind hier zwei verschiedene Zufallsvariablen.
Für die Summe von n verschiedenen Zufallsvariablen gilt:
Linearität: und sind hier Konstanten und eine Zufallsvariable.
, also auch
und
Erwartungswert von Produkten von unabhängigen Zufallsvariablen. und sind hier unabhängige Zufallsvariablen.
Für n voneinander unabhängige Zufallsgrößen gilt:
Wichtige Erwartungswerte
Verteilung | Dichte | Erwartungswert |
|---|---|---|
|
Beispielaufgabe
Laden
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Erwartungswert
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
