Die Division von Polynomen ist eine Verallgemeinerung der schriftlichen Division ganzer Zahlen.
Anwendungen finden Polynomdivisionen bei der Faktorisierung und Nullstellenbestimmung ganzrationaler Funktionen mindestens dritten Grades sowie bei der Berechnung von Asymptoten bei gebrochenrationalen Funktionen.

Bei der schriftlichen Division ganzer Zahlen berechnest du schrittweise dein Ergebnis. Die Division kann aufgehen (Rest ) oder nicht (Rest ungleich ).
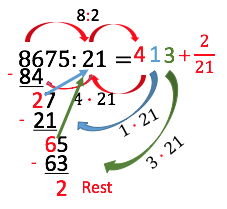
Die wesentlichen wiederholenden Rechenschritte des schriftlichen Dividierens sind:
Dividieren (hier ) als Startvorgang
Multiplizieren (hier ) als "Probe"
Subtrahieren (hier: ) als Restbildung
Vorbereitung zur Polynomdivision
Sowohl im Polynom des Dividenden als auch des Divisors sind gleichartige Glieder zusammenzufassen und alle Glieder nach fallenden Exponenten zu ordnen.
Beispiel
Bringe die Polynome folgender Divisionsaufgabe in eine zur Polynomdivision geeignete Form:
Lösung:
Vorgehen bei einer Polynomdivision
Die Polynomdivision vollzieht sich in der Regel in drei Schritten :
Division des höchsten Gliedes im Dividenden durch das höchste Glied im Divisor.
Multiplikation des Divisionsergebnisses mit dem gesamten Divisor.
Subtraktion zur Restbildung.
Eine Polynomdivision entfällt, wenn das Polynom des Dividenden von kleinerem Grad als das Polynom des Divisor ist. Das "Ergebnis" ist dann der Bruchterm einer gebrochenrationalen Funktion.
Beispiel:
Polynomdivision ohne Rest
Anhand des nachfolgenden Applets kannst du die Technik einer Polynomdivision schrittweise verstehen und nachvollziehen.
Dabei wirst du die Arbeitsschritte wiederfinden.
Polynomdivision mit Rest
Durch jeden der Arbeitsschritte wird der Grad des Restpolynoms kleiner.
Bleibt ein von verschiedenes Restpolynom übrig, das einen kleineren Grad als das Divisorpolynom hat, so ist die Polynomdivision "nicht aufgegangen".
Das Ergebnis der Division ist dann eine Summe aus einer ganzrationalen Funktion (Polynom) und einer echt gebrochenrationalen Funktion.
Du kannst dies schrittweise am nachfolgenden Applet nachvollziehen.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Polynomdivision
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
