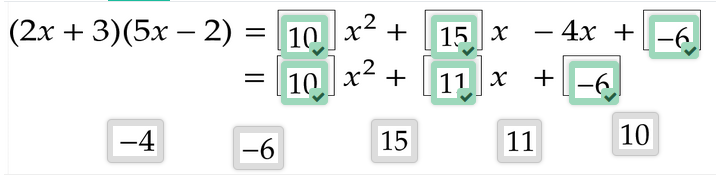Aufgaben zum Ausmultiplizieren
Hier findest du Übungsaufgaben zum Thema Ausmultiplizieren. Übe das Auflösen von Klammern, sowie Zusammenfassen der Terme!
- 1
Multipliziere aus
- 2
Löse auf
- 3
Multipliziere die Summen aus.
- 4
Multipliziere aus und fasse zusammen.
- 5
Überlege, aus wie vielen Summanden die Summe besteht, die man nach dem Ausmultiplizieren des Terms erhält.
Summanden - 6
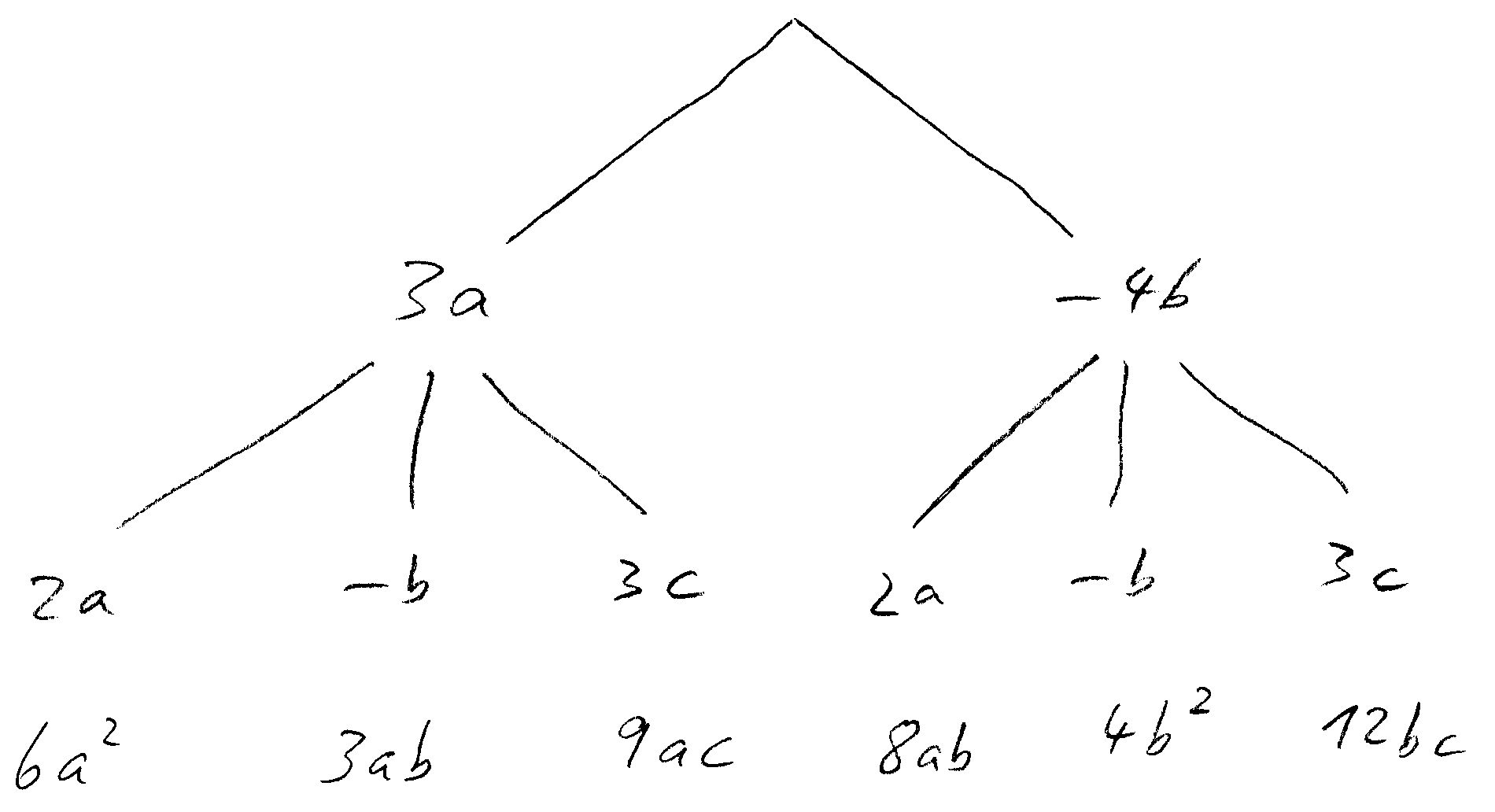
Benutze das Hilfsmittel des Baum-Schemas, um die folgenden Klammern auszumultiplizieren:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?