Dezimalbrüche sind Zahlen in Kommaschreibweise. Man begegnet ihnen überall im Alltag, sei es bei Preisschildern, bei Größenangaben oder auf dem Display des Taschenrechners.
Dezimalzahlen sind eine Möglichkeit, Bruchzahlen kompakt darzustellen.
Es gibt verschiedene Hilfen, mit Dezimalbrüchen zu rechnen. Man kann sie mithilfe der erweiterten Stellenwerttafel darstellen und so nach der ganzen Zahl und Dezimalstellen aufteilen oder den Dezimalbruch in gewöhnliche Brüche umwandeln.
Außerdem führt dieser Artikel die korrekte Sprechweise von Dezimalbrüchen ein. Wie man zwei Dezimalbrüche miteinander vergleicht, steht im Artikel Vergleich von Dezimalbrüchen.
Aufbau
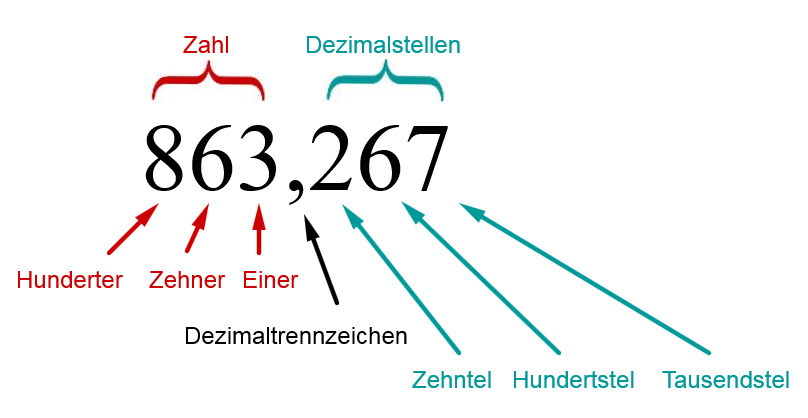
Jede Dezimalzahl ist nach dem Muster Zahl - Dezimaltrennzeichen - Dezimalstellen aufgebaut.
Das Dezimaltrennzeichen - in Deutschland und Österreich ein Komma, in der Schweiz ein Punkt - trennt die ganze(n) Zahl(en) von den Dezimalstellen.
Die erste Stelle nach dem Komma bezeichnet man als Zehntel (z), die zweite Stelle nach dem Komma als Hundertstel (h), die dritte Stelle nach dem Komma als Tausendstel (t). Die Namen der nächsten Nachkommastellen setzen sich zusammen aus dem Namen von einer Zehnerpotenz und der Silbe -tel oder -stel.
Dezimalbrüche im Alltag
Dezimalbrüche begegnen einem an jedem Tag im Alltag. Jedes mal, wenn man etwas kauft oder einen Preis liest, sieht man Dezimalbrüche.
Das Stellenwertsystem, das bei Dezimalbrüchen auftaucht, kennt man bereits vom Geld. Wie viel Geld man hat, hängt einmal von der Art der Münzen und auch von deren Anzahl ab. Genau so ist es auch bei Dezimalbrüchen: Je nachdem, an welcher Stelle hinter dem Komma eine Dezimalstelle steht, gibt die Ziffer eine unterschiedlich große Zahl an.

Betrachte nun 1-Euro-Münzen, 10-Cent-Stücke und 1 Cent-Stücke. Ein Euro ist genau so viel wert wie hundert 1-Cent-Stücke und genau so viel wert wie zehn 10-Cent-Stücke. Was die Hundertstel beim Dezimalbruch sind, sind beim Geld die 1-Cent-Stücke. Was die Zehntel beim Dezimalbruch sind, sind beim Geld die 10-Cent-Stücke. Man kann also beispielsweise den als Dezimalbruch geschriebenen Preis 1,72€ aufteilen in 1 1-Euromünze, 7 10-Cent-Stücke und 2 1-Cent-Stücke. Im Dezimalbruch entspricht das der ganzen Zahl 1, 7 Zehntel und 2 Hundertstel.
Dezimalbrüche in der Stellenwerttafel
Eine Möglichkeit Zahlen darzustellen ist die Stellenwerttafel. Dabei wird die Zahl in ihre Bestandteile nach den Bündelungseinheiten Einern, Zehnern, Hundertern und so weiter zerlegt und die Anzahl der Bündelungseinheiten wird jeweils in die Spalten der Stellenwerttafel eingetragen.
Die Spalten sind dementsprechend mit T (Tausender), H (Hunderter), Z (Zehner) und E (Einer) beschriftet.
Im Dezimalsystem sind jeweils 10 Einheiten einer Bündelungseinheit in der nächstgrößeren Bündelungseinheit zusammengefasst. So sind 10 Einer 1 Zehner, 10 Zehner 1 Hunderter, 10 Hunderter 1 Tausender etc.
Im Dezimalsystem sind jeweils 10 Einheiten einer Bündelungseinheit in der nächstgrößeren Bündelungseinheit zusammengefasst. So sind 10 Einer 1 Zehner, 10 Zehner 1 Hunderter, 10 Hunderter 1 Tausender etc.
Vielleicht hilft folgendes Bild, um sich die Bedeutung der Dezimalstellen vorzustellen: Man stellt sich einen Zehner als einen Geldsack vor, in dem sich 10 Einer-Münzen befinden. Ein Hunderter ist dann ein Sack, in den man 10 Zehner-Säcke gesteckt hat. Wenn man also einen Hunderter-Sack aufmacht, dann hat man zehn Zehnersäcke vor sich.
So ist die Zahl 207 zusammengesetzt aus 2 Hunderten, 0 Zehnern und 7 Einern, denn
In der Stellenwerttafel sieht die Darstellung so aus:
T | H | Z | E |
|---|---|---|---|
0 | 2 | 0 | 7 |
Diese Darstellung kann man erweitern, um auch kleinere Zahlen als 1 darzustellen.
Dazu fügt man rechts an die Stellenwerttafel neue Bündelungseinheiten an. Diese sind
das Zehntel oder , abgekürzt mit z
das Hundertstel oder , abgekürzt mit h
das Tausendstel oder , abgekürzt mit t.
Wie schon bei der einfachen Stellenwerttafel ist der Schritt zwischen zwei Bündelungseinheiten im Dezimalsystem der Faktor 10.
Die erweiterte Stellenwerttafel sieht nun so aus:
T | H | Z | E | z | h | t | |
|---|---|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 | 0 | 0 |
Um nun Dezimalbrüche darzustellen, zerlegt man wieder die Zahl in ihre Bündelungseinheiten. Als Beispiel betrachten wir den Dezimalbruch 1,83. Diese Zahl lässt sich aufteilen in
T | H | Z | E | z | h | t | |
|---|---|---|---|---|---|---|---|
1 | 8 | 3 | 0 |
Da kein einzelnes Tausendstel vorhanden ist, tragen wir eine 0 in die t-Spalte ein.
Dezimalbrüche und Brüche
Man kann alle Dezimalzahlen auch als Brüche schreiben.
Die ganze Zahl kann man auf verschiedene Arten zusammensetzen:
Hunderter oder
Zehner oder
Einer
Diese Überlegung kann man über das Dezimaltrennzeichen hinaus auch bei den Dezimalstellen anstellen.
Den Dezimalbruch 0,1 kann man auf verschiedene Arten zusammensetzen:
1 Zehntel, also oder
10 Hundertstel, also oder
100 Tausendstel, also
Macht es einen Unterschied, ob wir 0,1 oder 0,10 oder sogar 0,100 schreiben? Um das am besten zu sehen, betrachten wir die Dezimalbrüche als Brüche:
Die Brüche sind identisch, da du und jeweils auf kürzen kannst. Also sind die Dezimalzahlen 0,1 und 0,10 und 0,100 identisch.
Die Zahl vor dem Dezimaltrennzeichen gibt eine ganze Zahl an. Die erste Dezimalstelle nach dem Dezimaltrennzeichen gibt also an, wie viele Zehntel (z) zur ganzen Zahl addiert werden. Die zweite Dezimalstelle nach dem Dezimaltrennzeichen gibt an, wie viele Hundertstel (h) zur ganzen Zahl addiert werden. Die dritte Dezimalstelle nach dem Dezimaltrennzeichen gibt an, wie viele Tausendstel (t) zur ganzen Zahl addiert werden, und so weiter…
Wir betrachten als Beispiel die Zahl 5,086. Die ganze Zahl sind 5 Einer (E), nach dem Dezimaltrennzeichen folgen 0 Zehntel (z), 8 Hundertstel (h) und 6 Tausendstel (t), also
Die Tatsache, dass die Brüche und die gleiche Zahl darstellen, liegt daran, dass man sie kürzen kann. Das ist auch der Grund, warum man Nullen hinter der letzten Dezimalstelle der Zahl weglassen darf, also warum beispielsweise 1,6 = 1,60 ist, denn es ändert die Größe der Zahl nicht, wenn man 0 Hundertstel hinzufügt.
Periodische und nichtperiodische Dezimalbrüche
Man unterscheidet zwischen abbrechenden und periodischen Dezimalbrüchen. Ein abbrechender Dezimalbruch ist ein Bruch, dessen Nenner ein Produkt aus 2 und/oder 5 bzw. Potenzen davon ist. Unter einem periodischen Dezimalbruch versteht man einen Dezimalbruch, bei dem sich eine bestimmte Zahlenreihenfolge immer wiederholt.
Sprechweise von Dezimalbrüchen
Wenn man im Alltag an der Kasse 3,98€ bezahlt, so sagt man beispielsweise dazu "drei Euro achtundneunzig" oder auch "drei Komma achtundneunzig Euro". In der Mathematik liest man das anders. Hier sagt man zu 3,98€: "drei Komma neun acht Euro". Diese Sprechweise hilft dabei, Fehler und Missverständnisse zu vermeiden.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
