Wenn man die Funktionen mit Hilfe der Rechenregeln für Bruchterme umformt, ist das Ableiten einfacher.

$f(x)=\dfrac{4x^3}{3}$

$\phantom{f(x)}=\dfrac{4}{3}\cdot x^3$

Ziehe den Faktor vor den Bruch.

Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen.

$f'(x)=\dfrac{4}{3}\cdot 3\cdot x^2=4x^2$

Das heißt, die in der Grafik gesuchte Funktion ist $f'(x)=4x^2$.

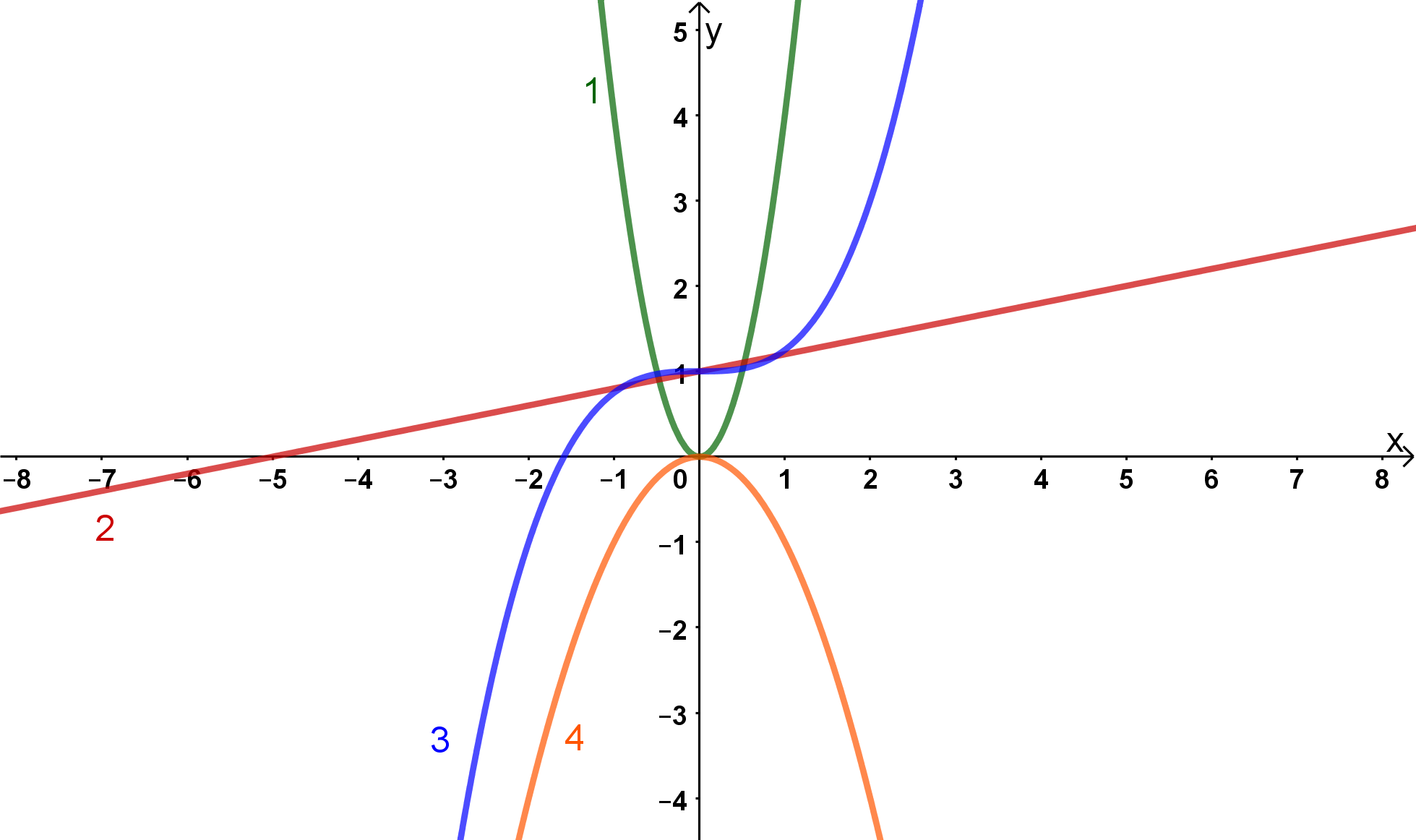
• Der Graph einer Funktion zweiten Grades ist eine Parabel.

• Deswegen kann man die Graphen $2$ und $4$ ausschließen, da diese beide keine Parabeln sind.

• Der Graph $3$ ist eine nach unten geöffnete Parabel. Bei einer nach unten geöffneten Parabel ist der Faktor vor dem $x^2$ negativ. Bei der Funktion $f'(x)$ ist der Faktor vor dem $x^2$ eine $4$ und damit positiv.

• Die gesuchte Funktion ist also die $1$.

Wenn man die Funktionen mit Hilfe der Rechenregeln für Bruchterme umformt, ist das Ableiten einfacher.

$g(x)=\dfrac{x^3+6x}{6}$$\phantom{g(x)}=\dfrac16\cdot(x^3+6x)$

Ziehe den Faktor $\dfrac16$ vor den Bruch.

Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen.

$g'(x)=\dfrac16\cdot(3\cdot x^2+6)$

$\phantom{g'(x)}=\dfrac12x^2+1$

Multipliziere $\dfrac16$ in die Klammer.

Das heißt, die in der Grafik gesuchte Funktion ist $g'(x)=\frac{1}{2}x^2+1$.

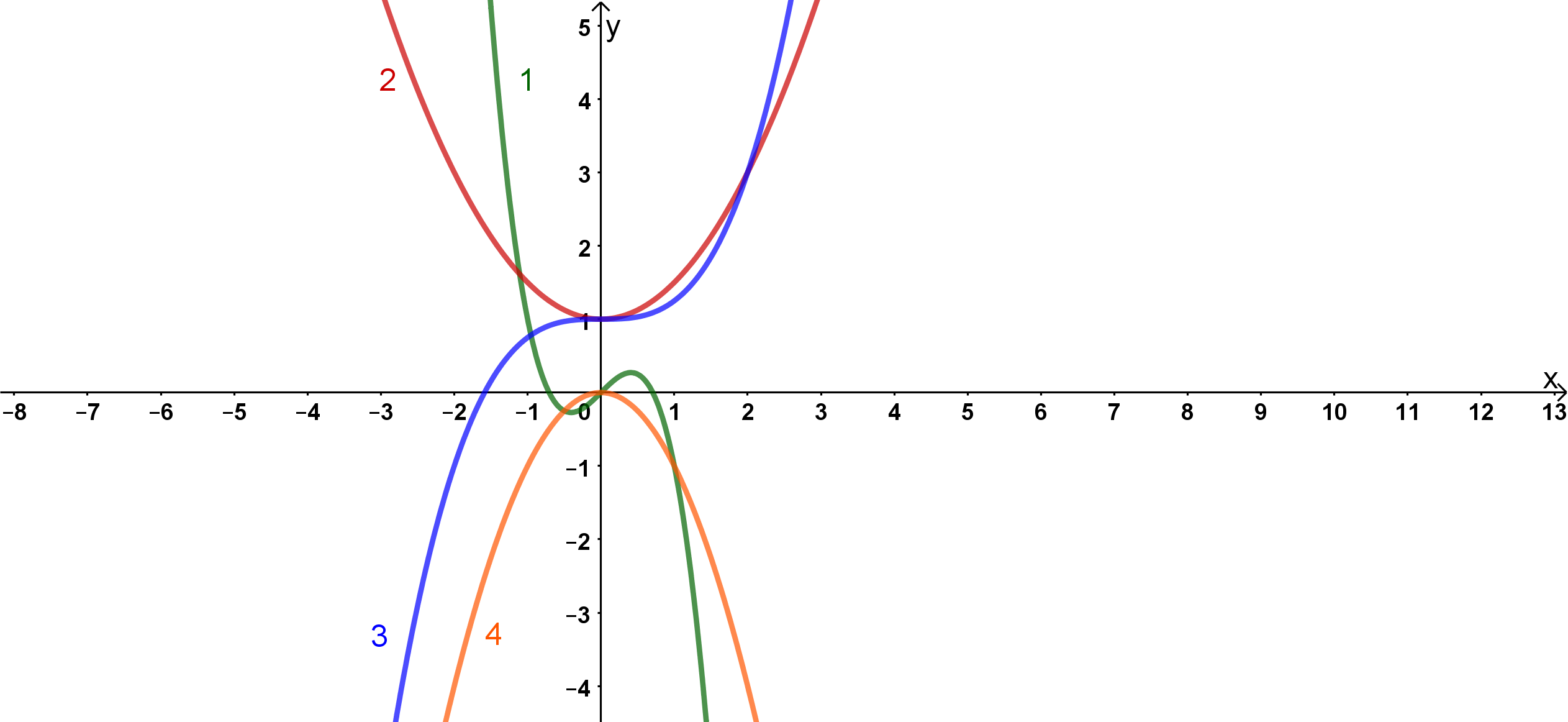
• Der Graph einer Funktion zweiten Grades ist eine Parabel.

• Deswegen kann man die Graphen $1$ und $3$ ausschließen, da diese beide keine Parabeln sind.

• Der Graph $4$ ist eine nach unten geöffnete Parabel. Bei einer nach unten geöffneten Parabel ist der Faktor vor dem $x^2$ negativ. Bei der Funktion $g'(x)$ ist $\dfrac12$ der Faktor vor dem $x^2$ und damit positiv.

• Die gesuchte Funktion ist also die $2$. Dies kann man auch gut an dem $+1$ in der Funktionsgleichung sehen. Sie sorgt für eine Verschiebung der Parabel, um $1$ nach oben entlang der y-Achse.

Du hast eine weitere Variante gefunden diese Aufgabe zu lösen? Dann schreib uns gerne in die Kommentare oder füge deine Variante der Lösung hinzu.

Wenn man die Funktionen mit Hilfe der Rechenregeln für Bruchterme umformt, ist das Ableiten einfacher.

$\def\arraystretch{2} \begin{aligned}h(x) &=\dfrac{x^4+108x}{108}\\ &= \dfrac{1}{108} \cdot (x^4 + 108 x)\end{aligned}$

Dafür bietet es sich an, dass du $\dfrac{1}{108}$ ausklammerst.

Das Ergebnis lässt sich nun mit Hilfe der Faktorregel, der Summenregel und der Ableitungsregel für Potenzfunktionen ableiten.

Zuerst werden die einzelnen Potenzfunktionen abgeleitet.

$\def\arraystretch{2} \begin{aligned} h´(x) &= \dfrac{1}{108} \cdot (4\cdot x^3 + 108) \\&= \dfrac{4}{108} \cdot x^3 + \dfrac{108}{108} \\&= \dfrac{1}{27} x^3 + 1 \end{aligned}$

Danach wird mit dem Faktor $\dfrac{1}{108}$ ausmultipliziert.

Du erhälst also $h´(x) = \dfrac{1}{27}x^3+1$.

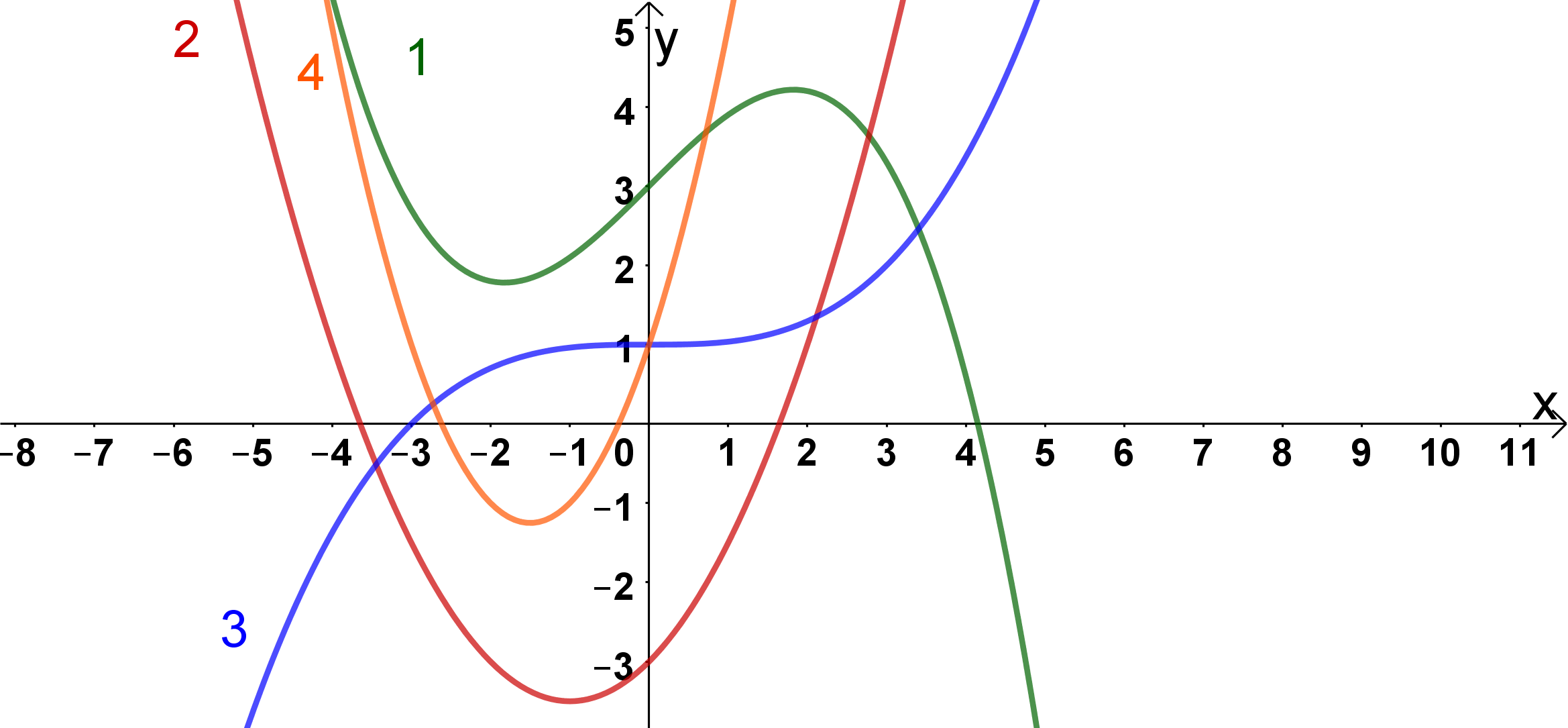
Die Ableitung $h´(x)$ ist eine Funktion dritten Grades.

Da es sich bei 2 und 4 um Parabeln und somit um Funktionen zweiten Grades handelt, fallen diese beiden Möglichkeiten schon mal weg.

$h´(x)$ hat mit $\dfrac{1}{27}$ einen positiven Vorfaktor und ist somit nach oben geöffnet. Deshalb fällt die Möglichkeit 1 ebenfalls weg. Die richtige Lösung ist somit der Graph 3.

$k(x)=-\dfrac{3x^5-10x^3-15x}{15}$

Wenn man die Funktionen mit Hilfe der Rechenregeln für Bruchterme umformt, ist das Ableiten einfacher. Klammere also zur Vereinfachung $\dfrac{1}{15}$ aus.

$\def\arraystretch{2} \begin{aligned}k(x)&=-\dfrac{3x^5-10x^3-15x}{15} \\ &= - \dfrac{1}{15} \cdot \left(3x^5-10x^3-15x \right) \end{aligned}$

Leite danach den entstandenen Term ab:

$\def\arraystretch{2} \begin{aligned} k´(x)&=-\dfrac{1}{15} \cdot ( 3 \cdot5 x^4 -10 \cdot 3 \cdot x^2 - 15) \\&= -\dfrac{1}{15} \cdot ( 15 x^4 - 30 x^2 - 15) \\&= -\dfrac{15}{15} x^4 +\dfrac{30}{15}x^2 + \dfrac{15}{15} \\&= -x^4 + 2x^2+1\end{aligned}$

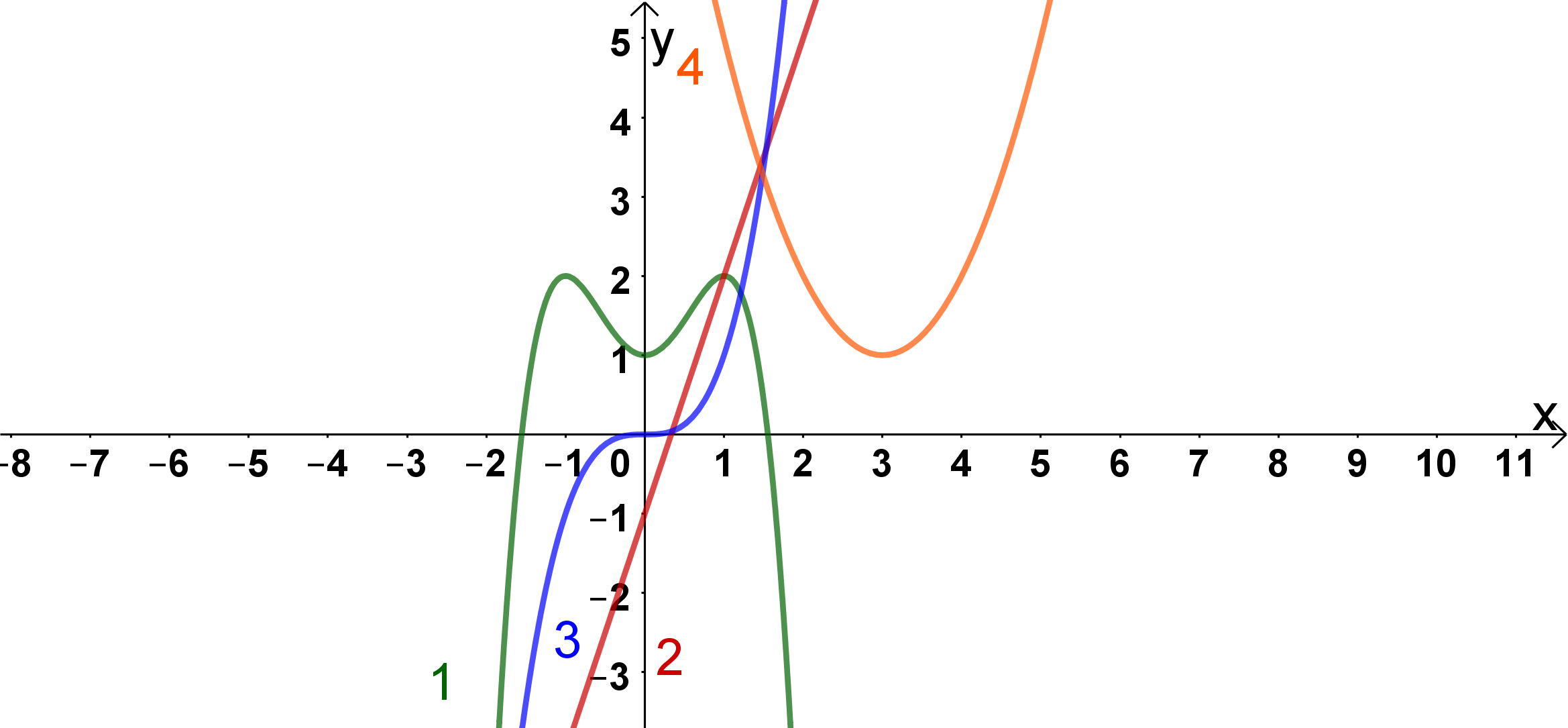
Die Ableitung von $k(x)$ ist also $k´(x)=-x^4+2x^2+1$ und somit eine Funktion 4. Grades.

Als Lösung fällt somit Graph 4 als Parabel (und somit Funktion 2. Grades) raus. Ebenso fällt Graph 2 als Gerade (und somit Funktion 1. Grades) raus. Die Graph 3 fällt als Funktion 3. Grades ebenso raus.

Der Graph 1 beschreibt eine Funktion, die nach unten geöffnet ist und entspricht somit (unter Verwendung der zuvor angeführten Punkte) der Lösung.

Wenn du die Funktionen mit Hilfe der Rechenregeln für Bruchterme umformst, ist das Ableiten einfacher.

$l(x)=-\dfrac{0{,}375x^4+\frac13x^3+\frac1{15}x^5+2x^2-3x}6$

Ziehe den Faktor $\dfrac16$ vor den Bruch.

$\phantom{l(x)}=-\dfrac16\cdot\left(0{,}375x^4+\dfrac13x^3+\dfrac1{15}x^5+2x^2-3x\right)$

Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen.

$l'(x)=-\dfrac16\cdot \left(0{,}375\cdot4\cdot x^3+\dfrac13\cdot 3\cdot x^2+\dfrac1{15}\cdot 5\cdot x^4+2\cdot2\cdot x-3\right)$

Fasst du den Term noch weiter zusammen und schreibst den Term wieder als Bruch erhälst du:

$l'(x)=-\dfrac{1{,}5x^3+x^2+\frac13x^4+4x-3}6$

$\phantom{l'(x)}=-\dfrac{\frac13x^4+1{,}5x^3+x^2+4x-3}6$

Ordne den Term auf dem Zähler nach dem Grad an.

Das heißt, die in der Grafik gesuchte Funktion ist $l'(x)=-\dfrac{\frac13x^4+1{,}5x^3+x^2+4x-3}6$ und somit eine Funktion 4. Grades.

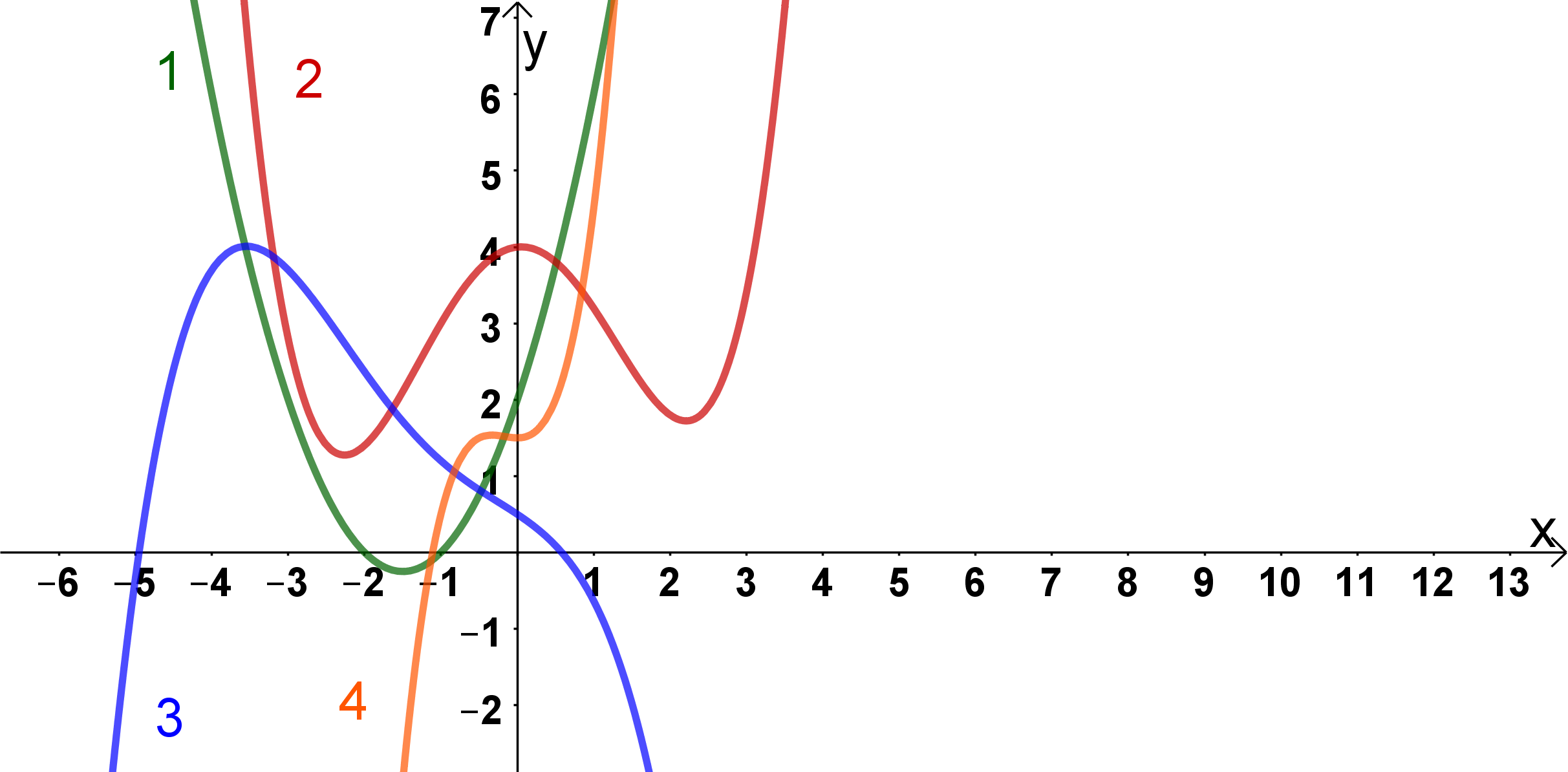
• Der Graph $1$ ist eine Parabel und gehört deswegen zu einer Funktion 2. Grades. Da $l'(x)$ allerdings eine Funktion 4. Grades ist, kannst du Graph $1$ ausschließen.

• Der Graph $4$ hat einen Wertebereich von $-\infty$ bis $+\infty$. Daraus kannst du folgern, dass der Grad der Funktion des Graphen $4$ ungerade ist. Da $l'(x)$ allerdings eine Funktion 4. Grades ist und damit einen geraden Grad besitzt, kannst du Graph $4$ ebenfalls ausschließen.

• Die Graphen $2$ und $3$ sind beides Graphen von Funktionen 4. Grades. Graph $2$ ist nach oben geöffnet und Graph $3$ ist nach unten geöffnet. Da $l'(x)$ ein Minus vor dem Leitkoeffizienten hat, muss der Graph von $l'(x)$ nach unten geöffnet sein. Somit kannst du Graph $2$ ausschließen und Graph $3$ ist der Graph der gesuchten Funktion.

Der Graph der gesuchten Funktion ist also der Graph $3$.