Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Gemischte Aufgaben zur Ableitung

Hier findest du unterschiedliche Aufgaben, um das Ableiten von Funktionen zu üben und welche Methoden zum Ableiten sich am besten eignen.

  1. 1

    Vereinfache folgende Funktionen so weit wie möglich und leite sie ab.

    1. f(x)=4x⋅xf(x)=\sqrt{4x}\cdot\sqrt x

    2. g(t)=4t+5t−3t−2tg(t)=4\sqrt t+5\sqrt t - 3\sqrt t-2\sqrt t

  2. 2

    Vereinfache die nachfolgenden Funktionsterme möglichst geschickt und bilde die Ableitungsfunktionen.

    5. l(x)=4x23⋅(2x+1)+4x+13⋅(2x+1)\displaystyle l(x)= \frac{4x^2}{3 \cdot (2x+1)}+\frac{4x+1}{3 \cdot (2x+1)}

    6. m(z)=(z−1z)2m(z) = \left(\dfrac{z-1}{z}\right)^2

  3. 3

    Vereinfache folgende Funktionen so weit wie möglich und leite sie ab.

    1. f(x)=(x+1)⋅(x−1)+1x3\displaystyle f(x)= \frac{(x+1)\cdot (x-1)+1}{x^3}

    2. g(z)=(z+3)2−6z−93z3g(z)=\dfrac{(z+3)^2-6z-9}{3z^3}

    3. h(s)=(s+1)2−s2(2s+1)2h(s)=\dfrac{(s+1)^2-s^2}{(2s+1)^2}

    4. k(t)=(t+2)⋅(t−2)(t2−4)3\displaystyle k(t)= \frac{(t+2)\cdot (t-2)}{(t^2-4)^3}

  4. 4

    Vereinfache folgende Funktionen so weit wie möglich und leite sie ab.

    1. f(x)=5x4−9x4−103x2+4x4f(x)=\dfrac{5}{x^4}-\dfrac{9}{x^4}-\dfrac{10}{3x^2}+\dfrac{4}{x^4}

    2. g(t)=103t3−3t3g(t)=\dfrac{10}{3t^3}-\dfrac{3}{t^3}

  5. 5

    Leite folgende Funktionen ab.

    1. f(x)=1xf(x)=\dfrac1x

    2. g(t)=34t4g(t)=\dfrac{34}{t^4}

    3. h(z)=34z4h(z)=\dfrac{3}{4z^4}

  6. 6

    Mathematicus hat hier die Funktion f(x)=1xf(x)=\dfrac1x mehrmals abgeleitet.

    Ableitungen von 1/x

    1. Versuche ohne weitere Rechnung die nächste Ableitung zu bestimmen.

    2. Mathematicus hat hier einige mögliche Formeln aufgeschrieben, wobei jeweils das n∈Nn\in \mathbb{N} für die Anzahl der Ableitungen steht. Welche der Formeln beschreibt die n-te Ableitung der Funktion f(x)=1xf(x)=\dfrac1x?

  7. 7

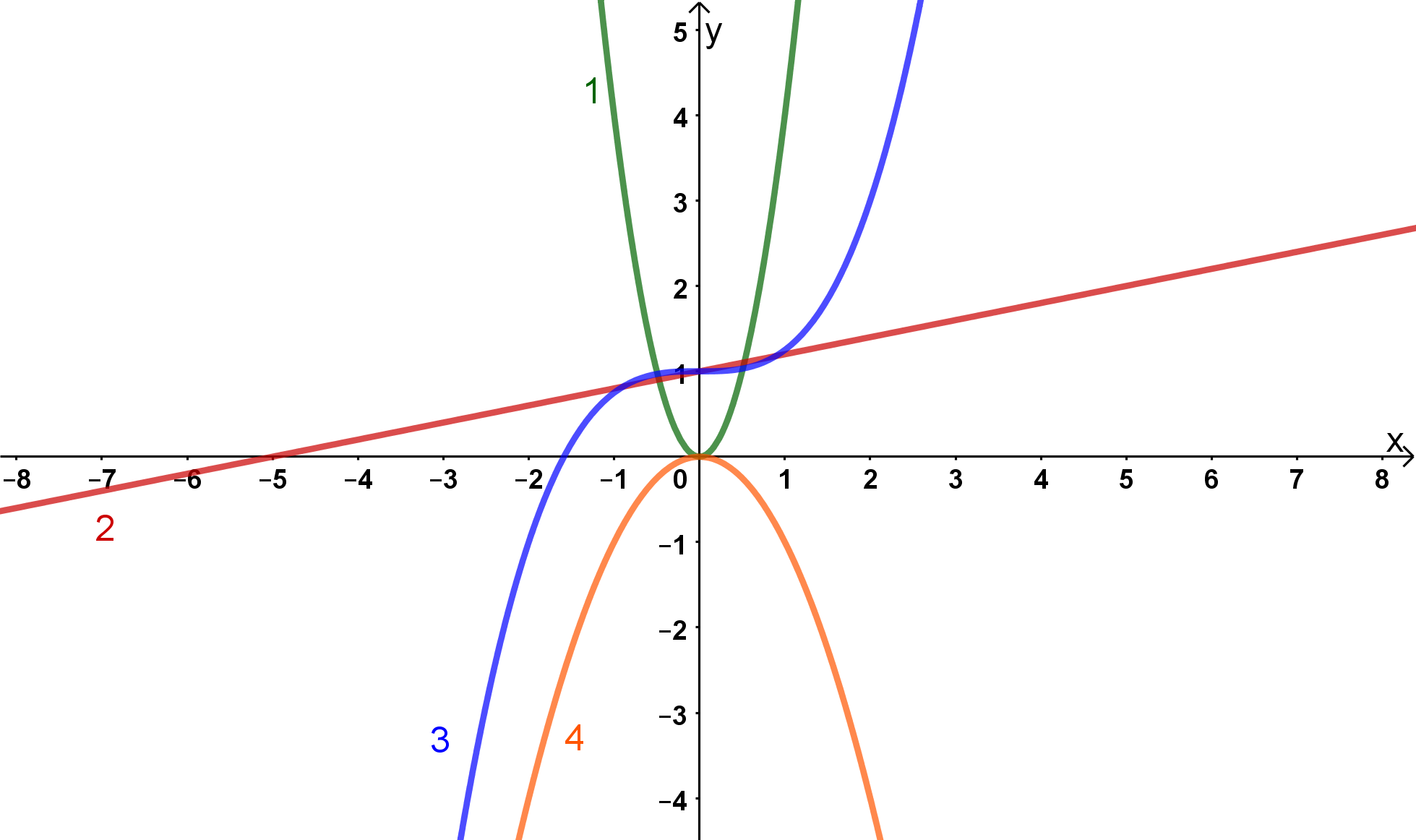
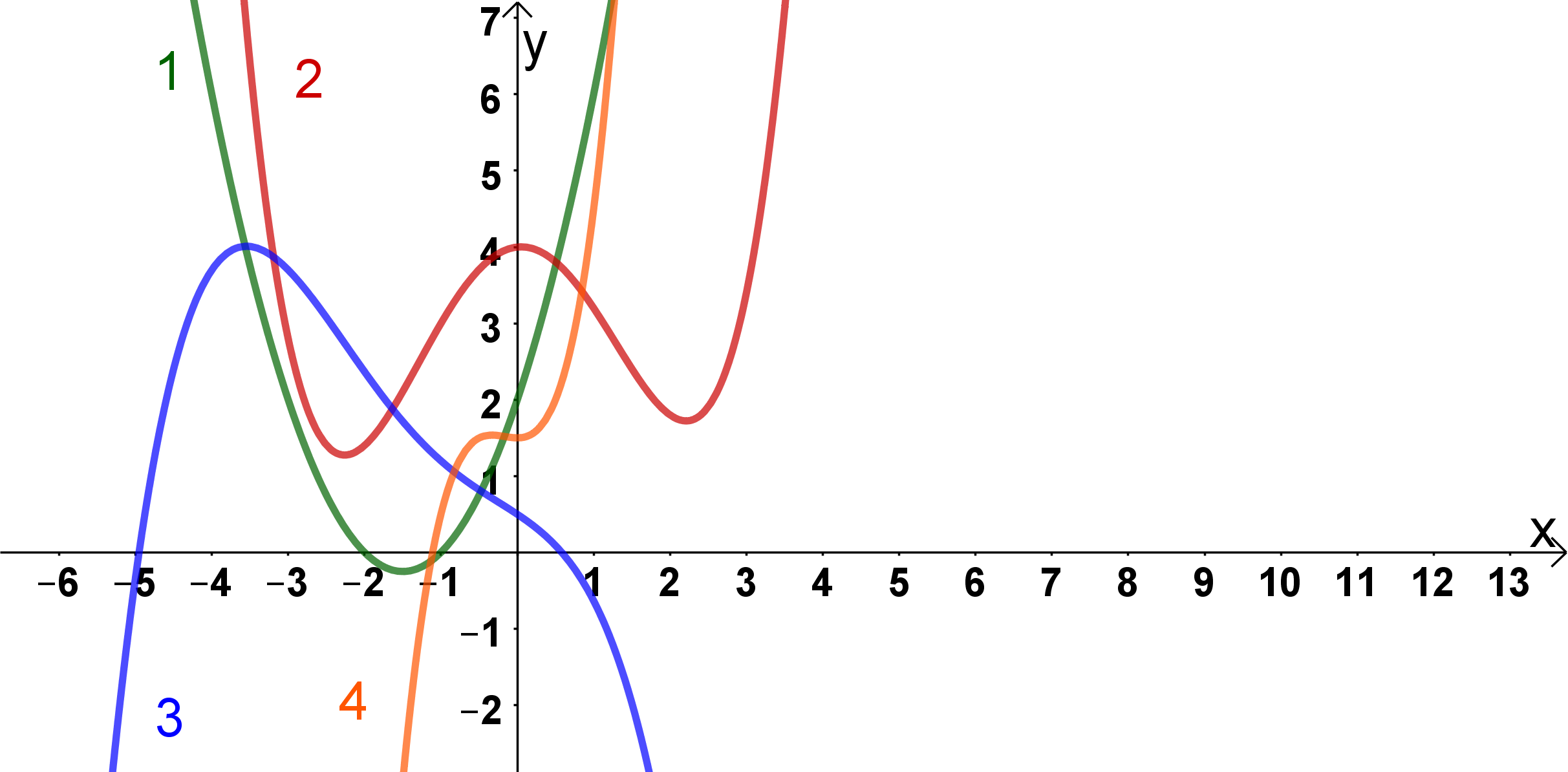
    Leite die folgenden Funktionen ab und entscheide welche der abgebildeten Graphen dem Funktionsgrahen der Ableitung der Funktion entsprechen. Fülle in den Feldern dafür den Funktionsnamen (1,2,31, 2, 3 oder 44) ein.

    Achtung: Die Graphen entsprechen der Ableitung der Funktion, nicht der Funktion selber.

    1. f(x)=4x33f(x)=\frac{4x^3}{3}

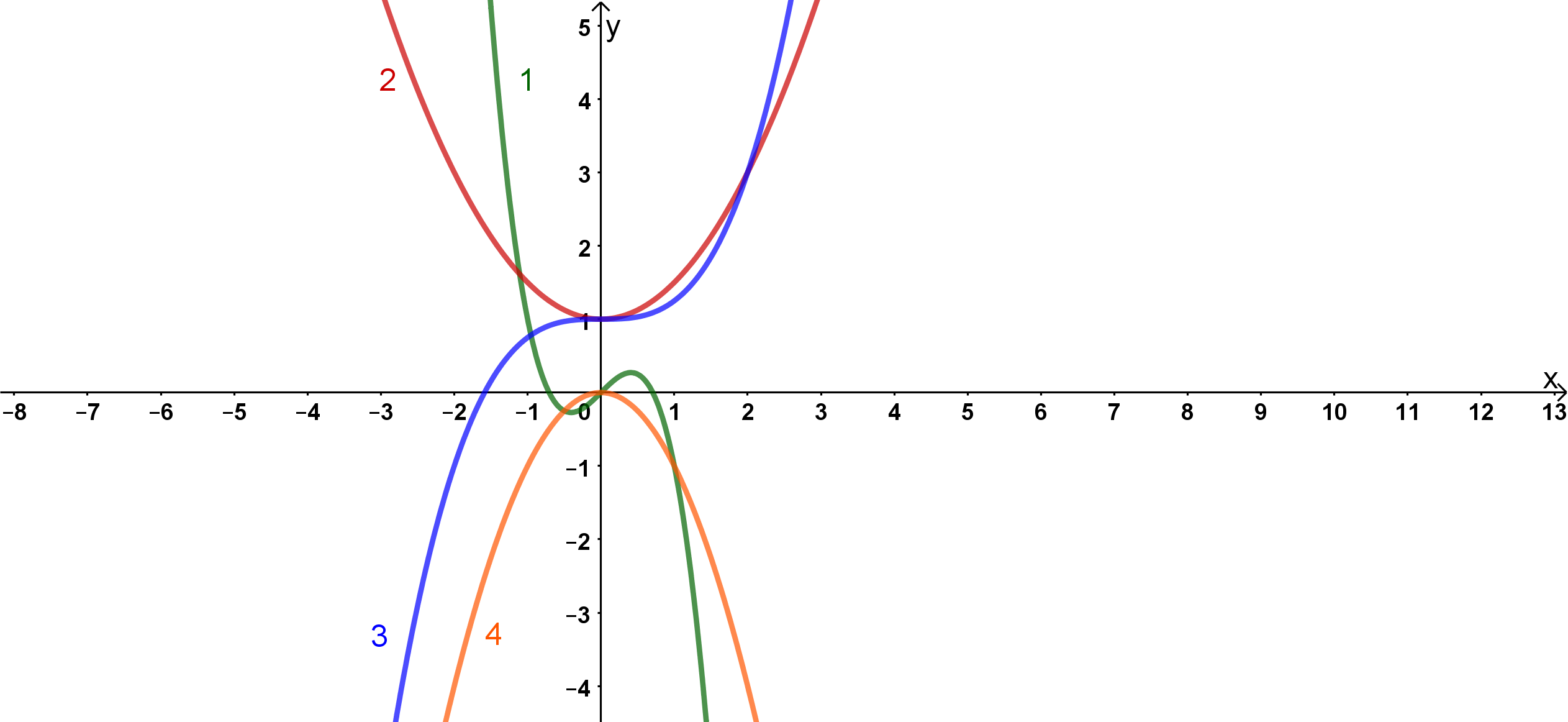
      Graph

    2. g(x)=x3+6x6g(x)=\frac{x^3+6x}{6}

      Graph

    3. h(x)=x4+108x108h(x)=\dfrac{x^4+108x}{108}

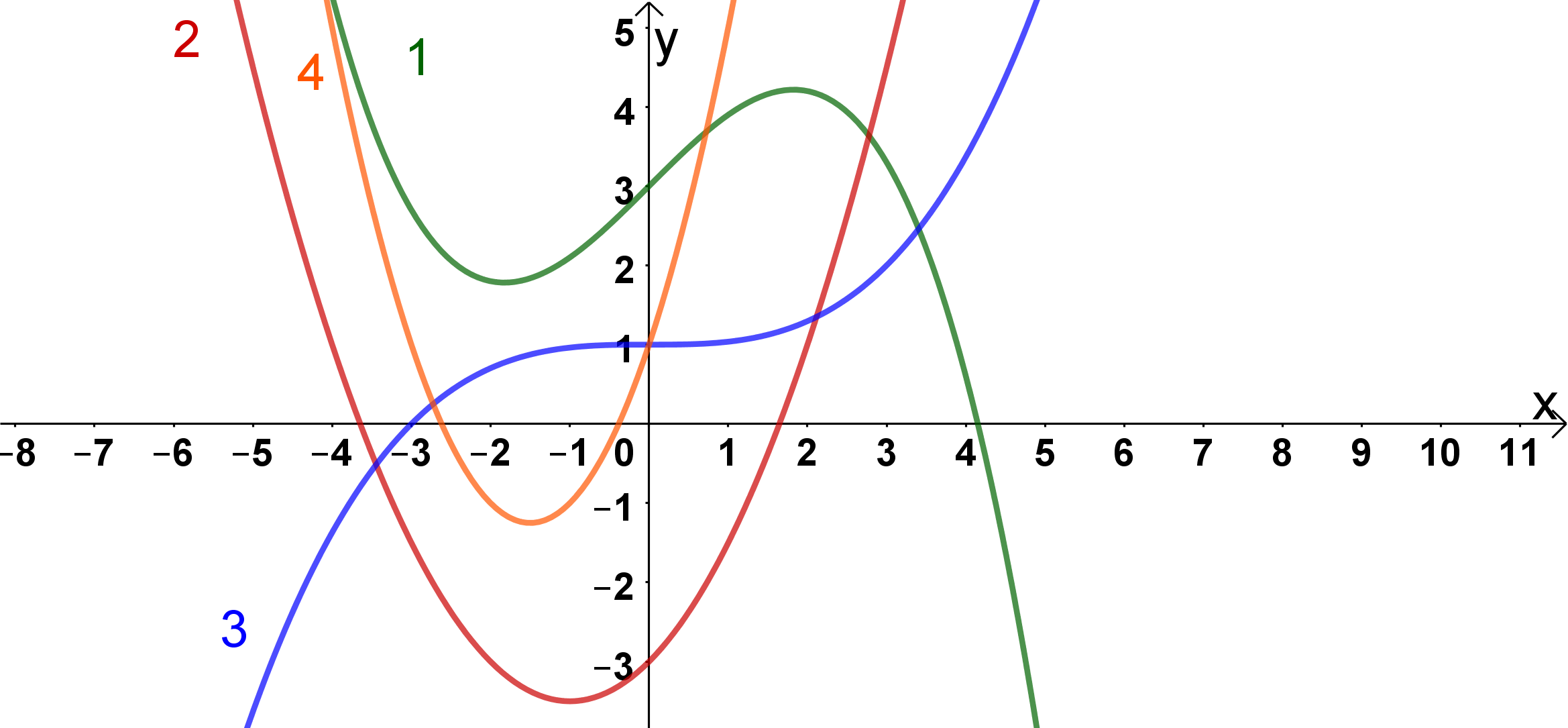
      Graphen

    4. k(x)=−3x5−10x3−15x15k(x)=-\dfrac{3x^5-10x^3-15x}{15}

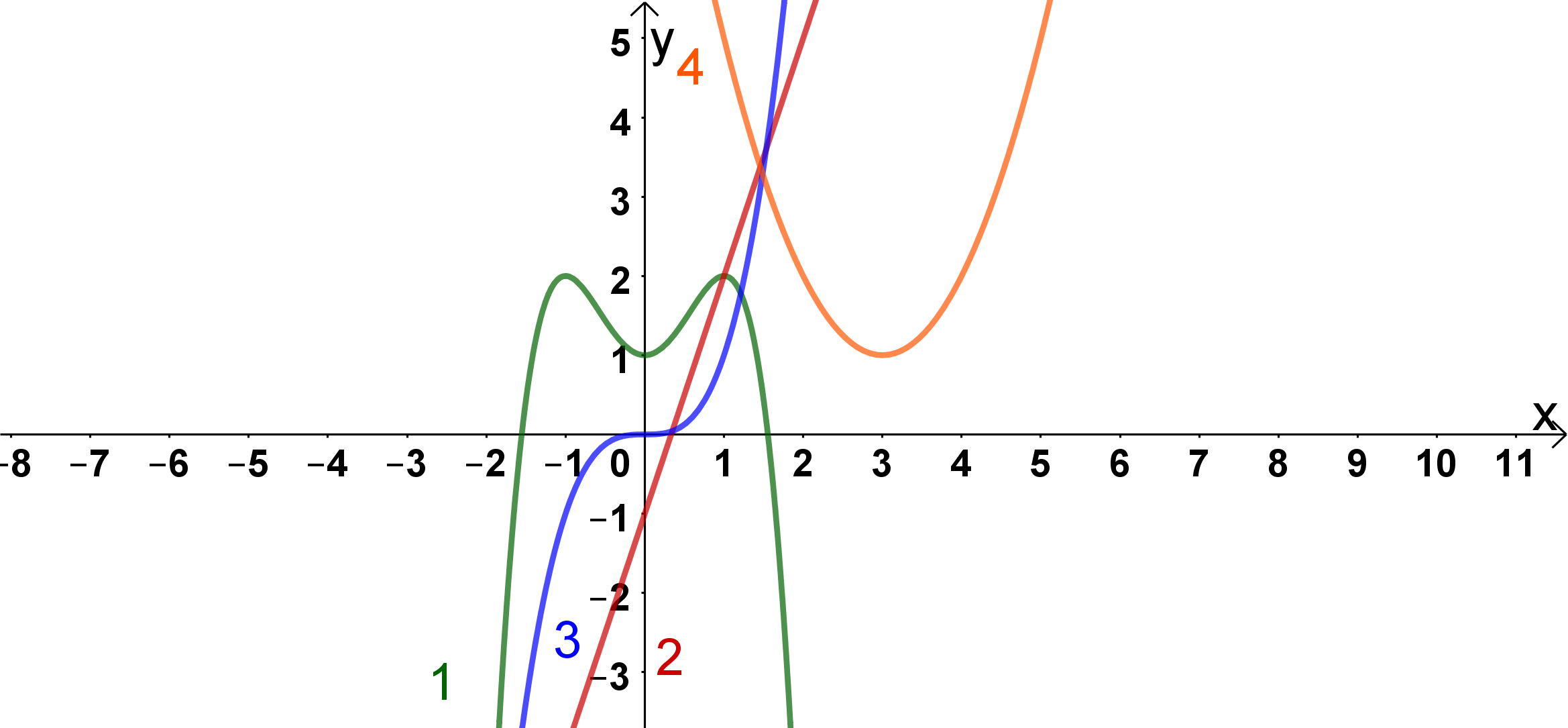
      Graph

    5. l(x)=−0,375x4+13x3+115x5+2x2−3x6l(x)=-\dfrac{0{,}375x^4+\frac13x^3+\frac1{15}x^5+2x^2-3x}6

      Graph

  8. 8

    Leite die Funktionen ab.

    1. f(t)=2t33f(t)=\dfrac{2t^3}{3}

    2. g(x)=−x48\displaystyle g(x)=-\dfrac{x^4}{8}

    3. h(z)=z6−63h(z)=\dfrac{z^6-6}{3}

  9. 9

    Vereinfache die Funktionen so weit wie möglich und leite sie ab.

    1. f(z)=3z214+2z27f(z)=\dfrac{3z^2}{14}+\dfrac{2z^2}{7}

    2. g(x)=7x212−x24g(x)=\dfrac{7x^2}{12}-\dfrac{x^2}{4}

    3. h(t)=−t33−t36\displaystyle h(t)= -\frac{t^3}{3}-\frac{t^3}{6}

  10. 10

    Welche Ableitungsregeln werden benötigt, um die Funktion

    abzuleiten?

  11. 11

    f(x)=−2x2(2−x)2f(x)= \dfrac{-2x^2}{(2-x)^2}

    Gesucht wird die Ableitung von f(x). Überlege zunächst, welche der im folgendern genannten Hilfsmittel und Ableitungsregeln nützlich sein können und leite die Funktion anschließend ab!

  12. 12

    f(x)=ln⁡(1+x1−x)+4f(x)=\ln\left ( \frac{1+x}{1-x} \right ) +4

    Überlege zunächst, welche der genannten Hilfsmittel und Ableitungsregeln nützlich sein können und leite die Funktion anschließend ab!

  13. 13

    Welche der folgenden Umformungen ist richtig? Leite die Funktion anschließend ab.

  14. 14

    Welche der folgenden Umformungen sind richtig? Leite die Funktion anschließend ab.

  15. 15

    Welche der folgenden Umformungen ist richtig? Leite danach die Funktion ab.

  16. 16

    Leite die Funktion f(x)=x2+sin⁡(x)3f(x)= \frac{x^2+\sin(x)}{3} ab.

  17. 17

    1. Welche der folgenden Umformungen sind richtig?

    2. Leite die Funktion ff ab.

  18. 18

    Leite die Funktion zunächst mit der Produkt- und Kettenregel ab und dann mit der Quotientenregel.

    f(x)=2x3−53x\displaystyle f(x) =\frac{2x^3-5}{3x}

  19. 19

    Berechne die Ableitung mit Summen-, Produkt und Kettenregel und überprüfe.Welches Verfahren bietet sich am ehesten an?

    1. f(x)=(−x−3)2{f(x)=(-x-3)}^2

    2. f(x)=(−x+2y)3f(x)={(-x+2y)}^3

  20. 20

    Bestimme die erste Ableitung von f(x)=4e2x⋅ex2f(x)=4e^{2x}\cdot e^{x^2} indem...

    • ... du zuerst die Potenzgesetze anwendest und dann ableitest.

    • ...du die Produktregel verwendest.

  21. 21

    Bestimme die ersten beiden Ableitungen der folgenden verknüpften Exponentialfunktionen

    1. f(x)=e−2x2f\left(x\right)=e^{-2x^2}

    2. f(x)=−0,5xe−x+1f(x)=-0{,}5xe^{-x}+1

    3. f(x)=(0,5x2+x)⋅e−2x2f(x)=(0{,}5x^2+x)\cdot e^{-2x^2}

  22. 22

    Bestimme alle Extrempunkte (mit Art) und Wendepunkte und gib die Monotonie- und Krümmungsintervalle an.

    1. f(x)=x2exf(x)=x^2e^x mit Df=RD_f=\R

    2. g(x)=(x2−4x+1)⋅e−xg(x)=(x^2-4x+1)\cdot e^{-x} mit Dg=RD_g=\R


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?