Aufgaben zur Diskussion von e-Funktionen

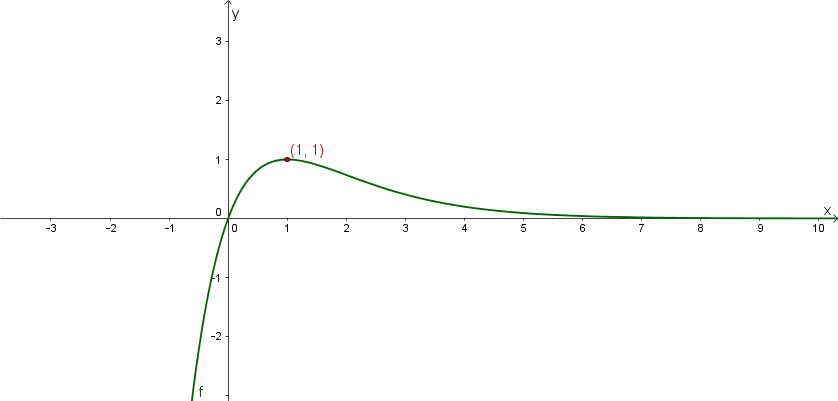
Gegeben ist die Funktion $f$ mit $f (x) = x \cdot e^{1 - x}$ .

In welchen Intervallen ist $f$ streng monoton wachsend?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten einer reellwertigen Funktion bestimmen
Eine reellwertige Funktion $f : [a, b] \to ℝ$ auf einem Intervall $[a, b]$ mit $a < b$ heißt
monoton wachsend auf $[a, b]$ , falls aus $a \leq x \leq y \leq b$ folgt, dass $f (x) \leq f (y)$ ist.
streng monoton wachsend auf $[a, b]$ , falls aus $a \leq x < y \leq b$ folgt, dass $f (x) < f (y)$ ist.
Kurz gesagt bedeutet monotones Wachstum: Je weiter du von $a$ ausgehend auf $b$ zugehst, desto größer werden die Funktionswerte von $f$ .
monoton fallend auf $[a, b]$ , falls aus $a \leq x \leq y \leq b$ folgt, dass $f (x) \geq f (y)$ ist.
streng monoton wachsend auf $[a, b]$ , falls aus $a \leq x < y \leq b$ folgt, dass $f (x) < f (y)$ ist.
Kurz gesagt bedeutet monotone Abnahme: Je weiter du von $a$ ausgehend auf $b$ zugehst, desto kleiner werden die Funktionswerte von $f$ .
Ist die betrachtete Funktion $f : [a, b] \to ℝ$ differenzierbar, so kannst du ihr Monotonieverhalten folgendermaßen bestimmen:
Ist $f^{'} (x) \geq 0$ (bzw. $> 0$ ) für alle $x$ in $[a, b]$ , so wächst $f$ monoton (bzw. streng) auf $[a, b]$ .
Ist $f^{'} (x) \leq 0$ (bzw. $< 0$ ) für alle $x$ in $[a, b]$ , so fällt $f$ monoton (bzw. streng monoton) auf $[a, b]$ .
Dieses Vorgehen kannst du auf differenzierbare Funktionen $f : ℝ \to ℝ$ verallgemeinern, indem du die Ableitung $f^{'}$ berechnest und $ℝ$ in größtmögliche Intervalle unterteilst, auf welchen $f^{'} \geq 0$ oder $f^{'} \leq 0$ ist.
In dieser Aufgabe ist
$f (x) = x \cdot e^{1 - x}$
$f$ ist laut Produkt- und Kettenregel differenzierbar, womit du also ihre Ableitung berechnen kannst:
$f^{'} (x) =$
Anwendung der Produktregel
$(x)^{'} \cdot e^{1 - x} + x \cdot (e^{1 - x})^{'} =$
Anwendung der Kettenregel unter Benutzung von $(e^{x})^{'} = \exp^{'} (x) = \exp (x) = e^{x}$ liefert:
$(e^{1 - x})^{'} =$
$(e x p (1 - x))^{'} =$
$\exp^{'} (1 - x) \cdot (1 - x)^{'} =$
$\exp (1 - x) \cdot (- 1) =$
$- e^{1 - x}$
Durch Einsetzen der Ableitung $(x)^{'} = 1$ erhältst du
$1 \cdot e^{1 - x} + x \cdot (- 1) \cdot e^{1 - x} =$
Hier kannst du den Ausdruck $e^{1 - x}$ herausheben:
$(1 - x) \cdot e^{1 - x}$
Dabei ist $e^{1 - x}$ für reelle $x$ immer positiv.
Daher hängt das Vorzeichen von $f^{'} (x)$ nur von dem Ausdruck $1 - x$ ab:
$1 - x > 0$ für $x < 1$ und
$1 - x < 0$ für $x > 1$ .
Insgesamt ist
$f^{'} (x) > 0$ für $x < 1$ und
$f^{'} (x) < 0$ für $x > 1$ .
Nach dem obigen Kriterium für differenzierbare Funktionen kannst du folgende Aussage zum Monotonieverhalten von $f$ angeben:
$f$ wächst streng monoton für $x < 1$ und fällt streng monoton für $x > 1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme alle Hoch- und Tiefpunkte des Graphen von $f$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Hoch- und Tiefpunkte berechnen
Aus Teilaufgabe a) weißt du bereits, dass $f^{'} (x) = (1 - x) \cdot e^{1 - x}$ ist. Berechne nun die Nullstellen der ersten Ableitung.
$f^{'} (x) = 0$
Setze für $f^{'} (x)$ ein.
$\Leftrightarrow (1 - x) \cdot e^{1 - x} = 0$
Desweiteren solltest du aus Teilaufgabe a) in Erinnerung behalten haben, dass $e^{1 - x} > 0$ ist. Somit ist die linke Seite der Gleichung genau dann gleich Null, wenn $1 - x = 0$ ist. Dies ist nur für $x = 1$ erfüllt.
$\Leftrightarrow x = 1$
$x = 1$ ist also der einzige Punkt von $f$ , der als Hoch- oder Tiefpunkt in Frage kommt.
Um zu entscheiden, ob es sich um einen Hoch- oder Tiefpunkt handelt, berechnest du die zweite Ableitung von $f$ .
$f^{''} (x) = ((1 - x) \cdot e^{1 - x})^{'}$
Wende die Produktregel an.
$= (1 - x)^{'} \cdot e^{1 - x} + (1 - x) \cdot (e^{1 - x})^{'}$
Wie in Teilaufgabe a) nutzt du zum Ableiten von $e^{1 - x}$ die Kettenregel und erhältst $(e^{1 - x})^{'} = - e^{1 - x}$ . Dies setzt du zusammen mit $(1 - x)^{'} = - 1$ ein.
$= - e^{1 - x} + (- 1) \cdot (1 - x) \cdot e^{1 - x}$
Hineinziehen des Minuszeichens in die Klammer.
$= - e^{1 - x} + (x - 1) \cdot e^{1 - x}$
Nun klammerst du $e^{1 - x}$ aus.
$= (- 1 + x - 1) \cdot e^{1 - x} = (x - 2) \cdot e^{1 - x}$
Nun setzt du $x = 1$ in die 2. Ableitung von $f$ ein.

$f^{''} (1) = (1 - 2) \cdot e^{1 - 1} = (- 1) \cdot \underset{= 1}{\underset{⏟}{e^{0}}} = - 1 < 0$
Da $f^{''} (1)$ kleiner als 0 ist, ist $x = 1$ ein Hochpunkt von $f$ .
Die Funktion $f (x) = x \cdot e^{1 - x}$ hat genau einen Hochpunkt bei $x = 1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne zuerst die Nullstellen der 1. Ableitung.
Überprüfe mithilfe der 2. Ableitung, ob es sich um Hoch- oder Tiefpunkte handelt.
Skizziere den Graphen von $f$ .

Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?