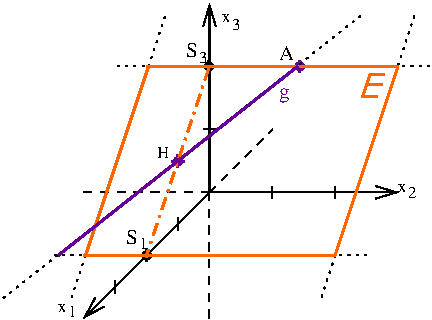
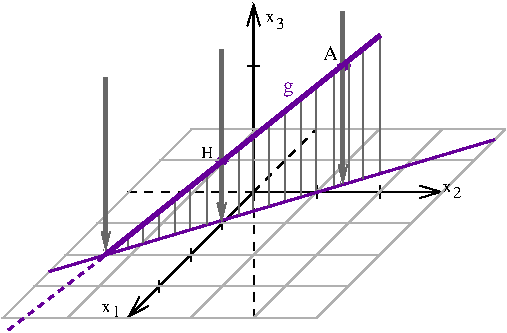
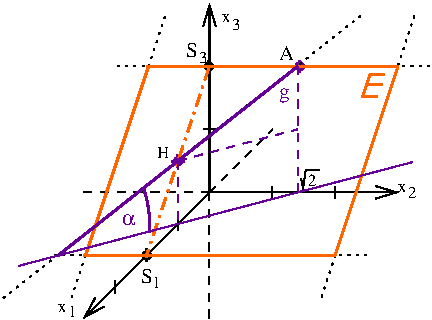
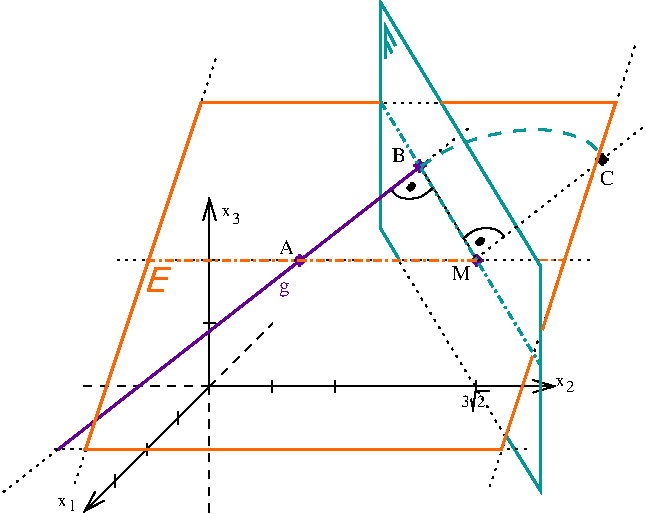
In einem kartesischen Koordinatensystem sind die Ebene , der Punkt und die Gerade , gegeben.
Beschreiben Sie, welche besondere Lage die Ebene im Koordinatensystem hat. Weisen Sie nach, dass die Ebene die Gerade enthält. Geben Sie die Koordinaten der Schnittpunkte von mit der -Achse und mit der -Achse an und veranschaulichen Sie die Lage der Ebene sowie den Verlauf der Geraden in einem kartesischen Koordinatensystem (vgl. Abbildung). (6 BE)
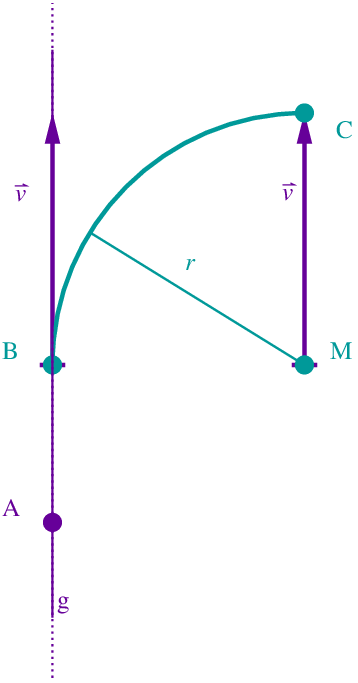
Die -Ebene beschreibt modellhaft eine horizontale Fläche, auf der eine Achterbahn errichtet wurde. Ein gerader Abschnitt der Bahn beginnt im Modell im Punkt und verläuft entlang der Geraden . Der Vektor beschreibt die Fahrtrichtung auf diesem Abschnitt.
Berechnen Sie im Modell die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt. (3 BE)
An den betrachteten geraden Abschnitt der Achterbahn schließt sich - in Fahrtrichtung gesehen - eine Rechtskurve an, die im Modell durch einen Viertelkreis beschrieben wird, der in der Ebene verläuft und den Mittelpunkt hat.
Das Lot von M auf g schneidet g im Punkt B. Im Modell stellt den Punkt der Achterbahn dar, in dem der gerade Abschnitt endet und die Kurve beginnt. Bestimmen Sie die Koordinaten von B und berechnen Sie den Kurvenradius im Modell. (5 BE)
Teilergebnis:
Das Ende der Rechtskurve wird im Koordinatensystem durch den Punkt beschrieben. Begründen Sie, dass für den Ortsvektor des Punkts gilt: (2 BE)
Ein Wagen der Achterbahn durchfährt den Abschnitt, der im Modell durch die Strecke und den Viertelkreis von nach dargestellt wird, mit einer durchschnittlichen Geschwindigkeit von . Berechnen Sie die Zeit, die der Wagen dafür benötigt, auf Zehntelsekunden genau, wenn eine Längeneinheit im Koordinatensystem in der Realität entspricht. (4 BE)