In der Abbildung sehen Sie ausschnittsweise den Graphen einer ganzrationalen Funktion f vom Grad 4 mit der Definitionsmenge Df=R.
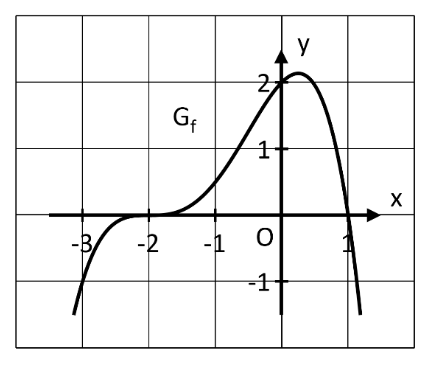
Geben Sie alle Nullstellen der Funktion f sowie jeweils deren Vielfachheit an. Bestimmen Sie mithilfe dieser Nullstellen eine Funktionsgleichung der Funktion f. Ganzzahlige Werte können der Abbildung entnommen werden. (4 BE)
Der Graph schneidet die x-Achse bei x1=−2 und x2=1.
Vielfachheit der Nullstellen
Die Nullstelle bei x=1 hat die Vielfachheit eins, denn es handelt sich um eine schneidende Nullstelle, die gleichzeitig kein Terrassenpunkt ist.
Die Nullstelle bei x=−2 ist ein Terrassenpunkt. Aufgrund des Grades 4 der Funktion f muss die Vielfachheit 3 sein (denn die Summe aller Vielfachheiten der Nullstellen ist maximal so groß wie der Grad).
Funktionsterm in Linearfaktorenform (Produktform)
Jede Nullstelle liefert einen Linearfaktor, indem man in die Form (x−xN) einsetzt, wobei xN die gefundene Nullstelle ist.
Die Vielfachheit kommt als Exponent außen an die Klammer.
Der Leitkoeffizient muss erst noch berechnet werden. Du kannst ihn mit a bezeichnen:
f(x)=a(x−1)(x−(−2))3=a(x−1)(x+2)3
Da die Funktion vom Grad 4 ist, gibt es keine weiteren Nullstellen oder Faktoren in der Produktform.
Setze nun einen Punkt ein, z.B. den y-Achsenabschnitt P(0∣2), um a zu bestimmen:
Die Position der Nullstellen kann aus dem Graph direkt abgelesen werden.
Die Vielfachheiten beider Nullstellen müssen ungerade sein, da es sich um schneidende Nullstellen handelt.
Daraus ergibt sich die Linearfaktorenform. Jede Nullstelle wird durch einen Linearfaktor dargestellt, die Vielfachheit liefert den Exponenten außerhalb des Linearfaktors. Nur der Leitkoeffizient muss dann noch durch Einsetzen eines weiteren Punktes bestimmt werden.
Entscheiden Sie anhand des Graphen Gf, ob die nachfolgenden Aussagen jeweils wahr oder falsch sind.
Begründen Sie jeweils Ihre Entscheidung.
a) f′(0)=−21
b) f′′(1)<0
c) f′′(−2)=f′(−2)
d)Wf=R
(4 BE)
f′(0)=−21
Das bedeutet, dass die Steigung am y-Achsenabschnitt negativ sein müsste, der Graph dort also fallen müsste. Diese Aussage ist falsch, denn der Graph steigt dort.
f′′(1)<0
Das bedeutet, dass der Graph bei x=1 rechtsgekrümmt ist. Diese Aussage ist wahr. (Fährst du mental mit einem Auto auf dem Graphen der Funktion entlang, so lenkst du an dieser Stelle nach rechts.)
f′′(−2)=f′(−2)
Diese Aussage ist wahr. Aufgrund der Vielfachheit 3 der Nullstelle x=−2 gilt f(−2)=f′(−2)=f′′(−2)=0.
Alternative Begründung: Da bei x=−2 eine waagerechte Tangente ist, gilt f′(−2)=0. Da es sich um einen Terrassenpunkt handelt, ist aber auch f′′(−2)=0
Wf=R
Diese Aussage ist falsch. Aufgrund des geraden Grades (f ist vom Grad 4) gibt es einen absoluten Hoch- oder Tiefpunkt und somit eine eingeschränkte Wertemenge. Im Graph ist zu sehen, dass es sich um einen absoluten Hochpunkt handelt.
Die erste Ableitung f′ liefert die Steigung und das Monotonieverhalten. Die zweite Ableitung f′′ beschreibt das Krümmungsverhalten.
Es gilt: f(x)=−41(x4+5x3+6x2−4x−8). Der Nachweis hierfür ist nicht erforderlich. Ermitteln Sie die Maßzahl des Flächeninhalts des Flächenstücks, das der Graph Gf mit den Koordinatenachsen im I. Quadranten des Koordinatensystems einschließt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integral
Bestimmtes Integral angeben
Der Graph verläuft im Intervall [0;1] im I. Quadranten. Benutze diese Intervallgrenzen als Grenzen für das Integral:
∫01f(x)dx=∫01(−41(x4+5x3+6x2−4x−8))dx
Stammfunktion von f bilden
Bilde eine Stammfunktion von f. Du kannst dich selbst kontrollieren: Wenn du dein Ergebnis ableitest, muss wieder f(x) entstehen.
∫01f(x)dx=[−41(51x5+45x4+2x3−2x2−8x)]01
Wert des bestimmten Integrals berechnen
Den Wert des bestimmten Integrals berechnest du, indem du die obere Grenze und die untere Grenze in die gefundene Stammfunktion einsetzt und die Ergebnisse voneinander subtrahierst:
∫01f(x)dx
=
[−41(51x5+45x4+2x3−2x2−8x)]01
=
F(1)−F(0)
↓
Arbeite vorteilhaft: F(0)=0 und 1n ist immer 1
=
(−41(51⋅15+45⋅14+2⋅13−2⋅12−8⋅1))−0
=
(−41(51+45+2−2−8))−0
↓
Bringe die Brüche durch Erweitern auf den gleichen Nenner, wandle auch -8 in einen Bruch um
=
−41(204+2025−20160)
↓
Bei gleichem Nenner kann man die Zähler addieren
=
−41⋅(−20131)
↓
Multipliziere: Zähler mal Zähler, Nenner mal Nenner.
Berechne den Wert des bestimmten Integrals, indem du die Ober- und die Untergrenze in die Stammfunktion einsetzt und die Ergebnisse voneinander subtrahierst. Hier ist Kopfrechnen und vor allem Bruchrechnen gefragt!
