Teil 1, Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

In der Abbildung sehen Sie ausschnittsweise den Graphen einer ganzrationalen Funktion f vom Grad 4 mit der Definitionsmenge $D_{f} = ℝ$ .

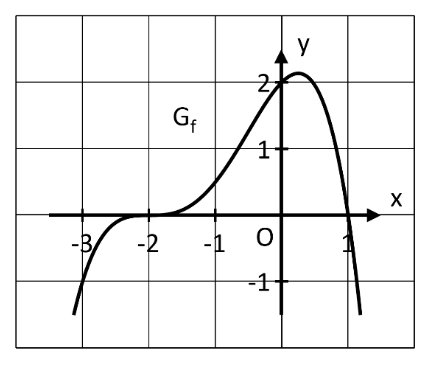
Geben Sie alle Nullstellen der Funktion f sowie jeweils deren Vielfachheit an. Bestimmen Sie mithilfe dieser Nullstellen eine Funktionsgleichung der Funktion f. Ganzzahlige Werte können der Abbildung entnommen werden. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearfaktorendarstellung
Position der Nullstellen
Der Graph schneidet die x-Achse bei $x_{1} = - 2$ und $x_{2} = 1$ .
Vielfachheit der Nullstellen
Die Nullstelle bei $x = 1$ hat die Vielfachheit eins, denn es handelt sich um eine schneidende Nullstelle, die gleichzeitig kein Terrassenpunkt ist.
Die Nullstelle bei $x = - 2$ ist ein Terrassenpunkt. Aufgrund des Grades 4 der Funktion f muss die Vielfachheit 3 sein (denn die Summe aller Vielfachheiten der Nullstellen ist maximal so groß wie der Grad).
Funktionsterm in Linearfaktorenform (Produktform)
Jede Nullstelle liefert einen Linearfaktor, indem man in die Form $(x - x_{N})$ einsetzt, wobei $x_{N}$ die gefundene Nullstelle ist.
Die Vielfachheit kommt als Exponent außen an die Klammer.
Der Leitkoeffizient muss erst noch berechnet werden. Du kannst ihn mit a bezeichnen:
$f (x) = a (x - 1) {(x - (- 2))}^{3} = a (x - 1) {(x + 2)}^{3}$
Da die Funktion vom Grad 4 ist, gibt es keine weiteren Nullstellen oder Faktoren in der Produktform.
Setze nun einen Punkt ein, z.B. den y-Achsenabschnitt $P (0 | 2)$ , um a zu bestimmen:
P in f:
↓
$2$ $=$ $a (0 - 1) {(0 + 2)}^{3}$
$2$ $=$ $- 8 a$ $: (- 8)$
$- \frac{1}{4}$ $=$ $a$
Insgesamt gilt für f also:
$f (x) = - \frac{1}{4} (x - 1) (x + 2)^{3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Position der Nullstellen kann aus dem Graph direkt abgelesen werden.
Die Vielfachheiten beider Nullstellen müssen ungerade sein, da es sich um schneidende Nullstellen handelt.
Daraus ergibt sich die Linearfaktorenform. Jede Nullstelle wird durch einen Linearfaktor dargestellt, die Vielfachheit liefert den Exponenten außerhalb des Linearfaktors. Nur der Leitkoeffizient muss dann noch durch Einsetzen eines weiteren Punktes bestimmt werden.
Entscheiden Sie anhand des Graphen $G_{f}$ , ob die nachfolgenden Aussagen jeweils wahr oder falsch sind.
Begründen Sie jeweils Ihre Entscheidung.
a) $f^{'} (0) = - \frac{1}{2}$
b) $f^{''} (1) < 0$
c) $f^{''} (- 2) = f^{'} (- 2)$
d) $W_{f} = ℝ$
(4 BE)

$f^{'} (0) = - \frac{1}{2}$
Das bedeutet, dass die Steigung am y-Achsenabschnitt negativ sein müsste, der Graph dort also fallen müsste. Diese Aussage ist falsch, denn der Graph steigt dort.
$f^{''} (1) < 0$
Das bedeutet, dass der Graph bei $x = 1$ rechtsgekrümmt ist. Diese Aussage ist wahr. (Fährst du mental mit einem Auto auf dem Graphen der Funktion entlang, so lenkst du an dieser Stelle nach rechts.)
$f^{''} (- 2) = f^{'} (- 2)$
Diese Aussage ist wahr. Aufgrund der Vielfachheit 3 der Nullstelle $x = - 2$ gilt $f (- 2) = f^{'} (- 2) = f^{''} (- 2) = 0$ .
Alternative Begründung: Da bei $x = - 2$ eine waagerechte Tangente ist, gilt $f^{'} (- 2) = 0$ . Da es sich um einen Terrassenpunkt handelt, ist aber auch $f^{''} (- 2) = 0$
$W_{f} = ℝ$
Diese Aussage ist falsch. Aufgrund des geraden Grades (f ist vom Grad 4) gibt es einen absoluten Hoch- oder Tiefpunkt und somit eine eingeschränkte Wertemenge. Im Graph ist zu sehen, dass es sich um einen absoluten Hochpunkt handelt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die erste Ableitung $f^{'}$ liefert die Steigung und das Monotonieverhalten. Die zweite Ableitung $f^{''}$ beschreibt das Krümmungsverhalten.

Es gilt: $f (x) = - \frac{1}{4} (x^{4} + 5 x^{3} + 6 x^{2} - 4 x - 8)$ . Der Nachweis hierfür ist nicht erforderlich. Ermitteln Sie die Maßzahl des Flächeninhalts des Flächenstücks, das der Graph $G_{f}$ mit den Koordinatenachsen im I. Quadranten des Koordinatensystems einschließt. (4 BE)

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
g ist eine ganzrationale Funktion vierten Grades mit der Definitionsmenge $D_{g} = ℝ$ .
In der Abbildung sehen Sie ausschnittsweise den Graphen der Ableitungsfunktion $g^{'}$ .
Ganzzahlige Werte können der Abbildung entnommen werden.
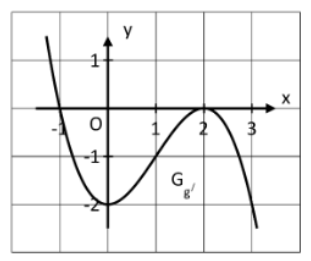
1. Geben Sie die Stellen an, an welchen der Graph der Funktion g Punkte mit horizontaler Tangente hat und benennen Sie jeweils die Art dieser Graphenpunkte. (2 BE)
  
  Nullstelle von $g^{'}$ bei $x = - 1$
  Da der Graph von $g^{'}$ bei dieser Nullstelle das Vorzeichen wechselt, handelt es sich um eine Extremstelle.
  Dass der Graph $G_{g^{'}}$ davor oberhalb der x-Achse verläuft, bedeutet, dass der Graph $G_{g}$ links von $x = - 1$ streng monoton steigt. Rechts von $x = - 1$ fällt der Graph von $G_{g}$ dann streng monoton, da $G_{g^{'}}$ unterhalb der x-Achse verläuft.
  Es handelt sich deshalb um einen Hochpunkt.
  Nullstelle von $g^{'}$ bei $x = 2$
  An dieser Nullstelle wechselt der Graph $G_{g^{'}}$ nicht das Vorzeichen, sondern verläuft weiterhin unterhalb der x-Achse.
  Das bedeutet, dass der Graph $G_{g}$ sowohl links von $x = 2_{}$ als auch rechts davon streng monoton fällt und bei $x = 2$ ein Terrassenpunkt von $G_{g}$ ist.
  Mögliches Aussehen von $G_{g}$
  Einen möglicher Graph von g siehst du unten im Koordinatensystem skizziert.
  Zum Einen sind abseits der Punkte mit waagerechten Tangenten keine weiteren Steigungen verwendet worden, zum Anderen kann der Graph der Stammfunktion beliebig nach oben oder unten verschoben sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Hat der Graph von $g$ eine waagerechte Tangente in einem Punkt, so hat der Graph der Ableitung $g^{'}$ dort eine Nullstelle.
  Je nachdem, ob $g^{'}$ an dieser Stelle das Vorzeichen wechselt, handelt es sich dann um einen Extrempunkt (Hoch- oder Tiefpunkt) oder um einen Terrassenpunkt.
2. Geben Sie mit Begründung die Wendestellen der Funktion g an. (3 BE)
  
  $G_{g^{'}}$ hat Extremstellen bei $x = 0$ und $x = 2$ . Dort liegen also die Wendestellen von $G_{g}$ , da $G_{g^{''}}$ dort Nullstellen hat.
  Mögliches Aussehen von $G_{g^{''}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Graph von g hat einen Wendepunkt, wenn $g^{''} (x) = 0$ (und der Graph $G_{g^{''}}$ dort das Vorzeichen wechselt).
  Das ist genau dann der Fall, wenn Der Graph der Ableitungsfunktion $G_{g}$ einen Extrempunkt (keinen Terrassenpunkt!) hat.
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben sind Auszüge aus zwei Wertetabellen zu zwei Funktionen h und k mit der Definitionsmenge $D_{h} = D_{k} = ℝ_{0}^{+}$ . Für die fehlenden Funktionswerte in den folgenden Tabellen gilt $h (x) \geq 0$ und $k (x) \geq 0$ .
Tabelle 1
x
0
2
4
h(x)
7
5
Tabelle 2
x
0
2
4
k(x)
9
15
Entscheiden Sie begründet, welcher der folgenden Funktionsterme zu Tabelle 1 bzw. zu Tabelle 2 gehört.
A) $8 - 3^{0,5 x}$
B) $- x + 7$
C) $3^{0,5 x} + 6$
D) $x + 7$
Geben Sie dann die fehlenden Tabellenwerte an. (5 BE)

Term von h
Setzt man $x = 0$ und $x = 2$ in A und B ein, so erhält man die korrekten Werte $y = 7$ beziehungsweise $y = 5$
Allerdings erhält man bei Term A für $x = 4$ eine negative Zahl, was laut Aufgabenstellung nicht zugelassen ist ( $h (x) \geq 0)$ :
$A) 8 - 3^{0,5 \cdot 4} = 8 - 3^{2} = 8 - 9 = - 1$
Deshalb bleibt nur Term B, der einen positiven Funktionswert für $x = 4$ hat:
$B) - 4 + 7 = 3$
Term von k
Erneut erhält man für $x = 2$ für die Terme C und D die gleichen Termwerte
Allerdings erhält man für $x = 4$ bei D nicht den korrekten Wert:
$D) 4 + 7 = 11$
Bei C widerrum schon:
$C) 3^{0,5 \cdot 4} + 6 = 3^{2} + 6 = 9 + 6 = 15$
Der fehlende Funktionswert lautet:
$3^{{0,5}^{0}} + 6 = 3^{0} + 6 = 1 + 6 = 7$
Bestimme die Funktionswerte für $x = 2$ und vergleiche mit den Tabellen.
Bestimme dann für die passenden Terme die Werte für $x = 0$ bzw. $x = 4$ .
Falls noch mehr als ein Kandidat übrig bleibt, löse über die Angabe $h (x) \geq 0$ bzw. $k (x) \geq 0$ , indem du den fehlenden Funktionswert bestimmst.

x	0	2	4
h(x)	7	5

x	0	2	4
k(x)		9	15

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$\int_{0}^{1} f (x) d x$
$=$	${[- \frac{1}{4} (\frac{1}{5} x^{5} + \frac{5}{4} x^{4} + 2 x^{3} - 2 x^{2} - 8 x)]}_{0}^{1}$
$=$	$F (1) - F (0)$
	↓ Arbeite vorteilhaft: $F (0) = 0$ und $1^{n}$ ist immer 1
$=$	$(- \frac{1}{4} (\frac{1}{5} \cdot 1^{5} + \frac{5}{4} \cdot 1^{4} + 2 \cdot 1^{3} - 2 \cdot 1^{2} - 8 \cdot 1)) - 0$
$=$	$(- \frac{1}{4} (\frac{1}{5} + \frac{5}{4} + 2 - 2 - 8)) - 0$
	↓ Bringe die Brüche durch Erweitern auf den gleichen Nenner, wandle auch -8 in einen Bruch um
$=$	$- \frac{1}{4} (\frac{4}{20} + \frac{25}{20} - \frac{160}{20})$
	↓ Bei gleichem Nenner kann man die Zähler addieren
$=$	$- \frac{1}{4} \cdot (- \frac{131}{20})$
	↓ Multipliziere: Zähler mal Zähler, Nenner mal Nenner.
$=$	$\frac{131}{80}$

Teil 1, Analysis

Position der Nullstellen

Vielfachheit der Nullstellen

Funktionsterm in Linearfaktorenform (Produktform)

Hast du eine Frage oder Feedback?

$f^{'} (0) = - \frac{1}{2}$

$f^{''} (1) < 0$

$f^{''} (- 2) = f^{'} (- 2)$

$W_{f} = ℝ$

Hast du eine Frage oder Feedback?

Bestimmtes Integral angeben

Stammfunktion von f bilden

Wert des bestimmten Integrals berechnen

Hast du eine Frage oder Feedback?

Nullstelle von $g^{'}$ bei $x = - 1$

Nullstelle von $g^{'}$ bei $x = 2$

Mögliches Aussehen von $G_{g}$

Hast du eine Frage oder Feedback?

Mögliches Aussehen von $G_{g^{''}}$

Hast du eine Frage oder Feedback?

Term von h

Term von k

P in f:
	↓
$2$	$=$	$a (0 - 1) {(0 + 2)}^{3}$
$2$	$=$	$- 8 a$	$: (- 8)$
$- \frac{1}{4}$	$=$	$a$

Teil 1, Analysis

Position der Nullstellen

Vielfachheit der Nullstellen

Funktionsterm in Linearfaktorenform (Produktform)

Hast du eine Frage oder Feedback?

f′(0)=−12

f′′(1)<0

f′′(−2)=f′(−2)

Wf=ℝ

Hast du eine Frage oder Feedback?

Bestimmtes Integral angeben

Stammfunktion von f bilden

Wert des bestimmten Integrals berechnen

Hast du eine Frage oder Feedback?

Nullstelle von g′ bei x=−1

Nullstelle von g′ bei x=2

Mögliches Aussehen von Gg

Hast du eine Frage oder Feedback?

Mögliches Aussehen von Gg′′

Hast du eine Frage oder Feedback?

Term von h

Term von k

$f^{'} (0) = - \frac{1}{2}$

$f^{''} (1) < 0$

$f^{''} (- 2) = f^{'} (- 2)$

$W_{f} = ℝ$

Nullstelle von $g^{'}$ bei $x = - 1$

Nullstelle von $g^{'}$ bei $x = 2$

Mögliches Aussehen von $G_{g}$

Mögliches Aussehen von $G_{g^{''}}$