Aufgabe 1A
Gegeben ist die in definierte Funktion mit . Für die erste Ableitungsfunktion von gilt:
Skizzieren Sie den Graphen von in Abbildung 1.
Beschreiben Sie, wie der Graph von aus dem Graphen von erzeugt werden kann. (4 BE)
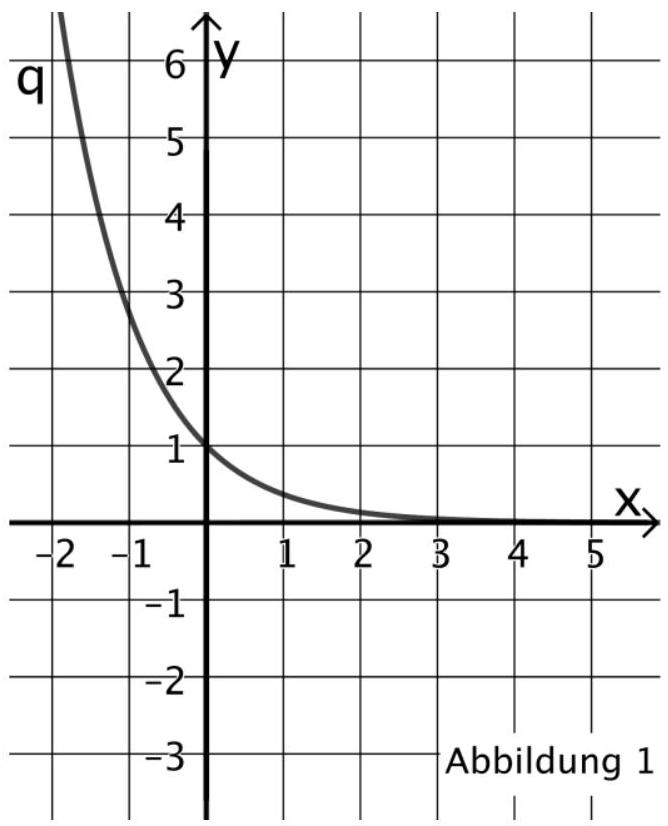
Zeigen Sie, dass mit eine Tangente an den Graphen von an der Stelle 0 ist. (3 BE)
Geben Sie die geometrische Bedeutung der Gleichung an.
Geben Sie den Wert von an. (3 BE)
Gegeben ist die in definierte Funktion mit .
Weiterhin gilt:
Berechnen Sie den Abstand der beiden Extrempunkte des Graphen von . (6 BE)
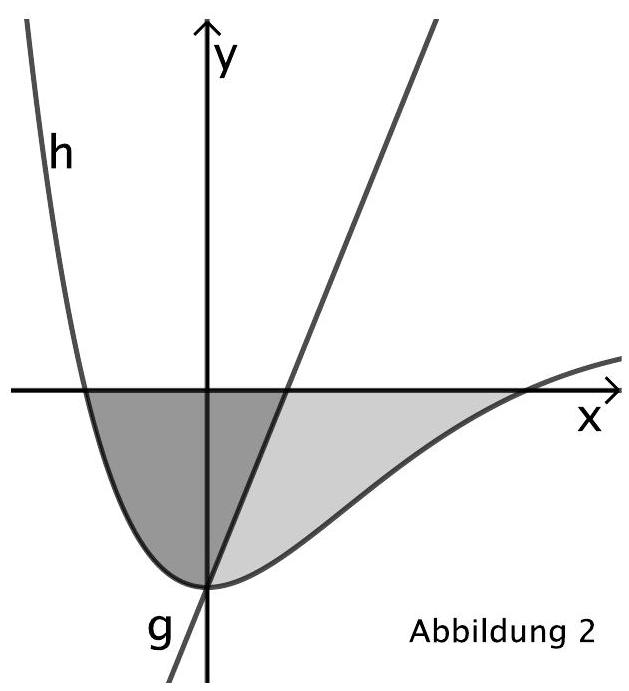
Der Graph von schließt mit der -Achse eine Fläche ein. Die Gerade mit teilt die Fläche in zwei gleich große Teilflächen. Die Abbildung 2 veranschaulicht die Situation.
Bestimmen Sie den Wert für . (6 BE)
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in definierte Funktion mit
beschreibt für die momentane Durchflussrate des Wassers an einer Messstelle. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Sekunden und die momentane Durchflussrate in Kubikmetern pro Sekunde . Abbildung 3 zeigt den Graphen von
Bestimmen Sie die momentane Durchflussrate für denjenigen Zeitpunkt, zu dem sie am stärksten abnimmt. (5 BE)
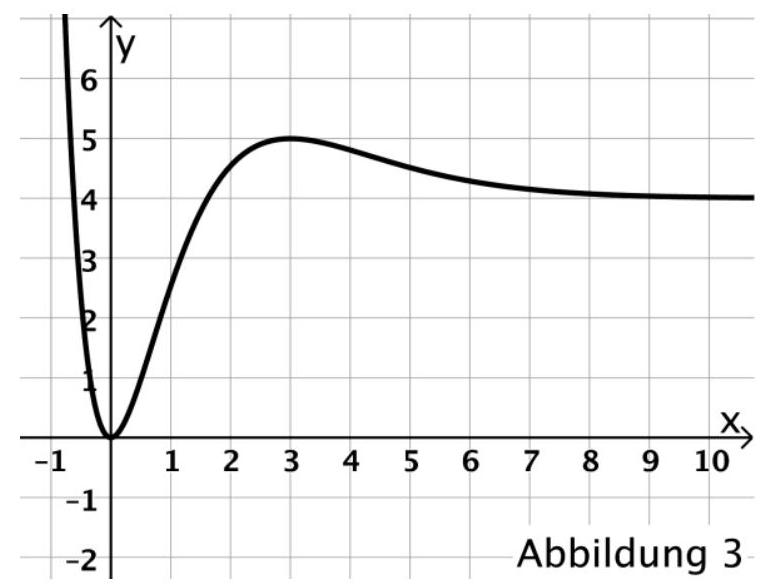
Betrachtet wird der Zeitraum der ersten zehn Sekunden nach Beobachtungsbeginn. Es gilt:
Für den betrachteten Zeitraum beträgt die mittlere Durchflussrate etwa .
Beschreiben Sie die graphische Bedeutung der obigen Aussage und veranschaulichen
Sie geeignete Flächen in der Abbildung 3. (5 BE)
Die Tangente an den Graphen von im Punkt wird mit bezeichnet.
Interpretieren Sie die folgende Aussage im Sachzusammenhang: (3 BE)
Für alle Werte von mit gilt .
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen



