Aufgaben zur Polynomfunktion - lernen mit Serlo!

Untersuche den Graphen $G_{f}$ der Funktion $f$ mit $f (x) = - 3 x^{4} - 2 x^{2} + 5$ soweit, sodass du ihn zeichnen kannst.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Ohne Wertetabelle ist es immer geschickt, sich über den Verlauf des Graphens Gedanken zu machen. Hilfreich hierbei sind vor allem erst einmal Nullstellen. Danach schaust du dir das Verhalten der Funktion im Unendlichen an.Um die Nullstellen herauszufinden gibt es zwei Möglichkeiten. Einmal kann man sie bei Polynomen mit einem Grad größer als zwei mit der Polynomdivision herausfinden oder bei dem Grad vier bietet sich auch die Substitution an.

Lösung 1: mit Polynomdivision

1. Schritt: Nullstellen raten

Schaue dir beim raten von Nullstellen die letzte Ziffer ohne ein $x$ an, wie kannst du die $5$ in ein Produkt aufteilen? Zum Beispiel in $1$ und $5$ . Probiere es mit $1$ : Super, eine Nullstelle gefunden!

2. Schritt: Polynomdivision um weitere Nullstellen zu finden

(- 3 x^{4} - 2 x^{2} + 5) : (x - 1) = - 3 x^{3} - 3 x^{2} - 5 x - 5

(- 3 x^{3} - 3 x^{2} - 5 x - 5) : (x + 1) = - 3 x^{2} - 5

- 3 x^{2} - 5 = 0

- 3 x^{2} = 5

x^{2} = \frac{5}{- 3}

Jetzt sollte man die Wurzel ziehen um auf das $x$ zu kommen. Dann würde aber etwas negatives unter der Wurzel stehen, dies ist nicht erlaubt. Also gibt es keine weitere Nullstelle.

3. Schritt: Verhalten im Unendlichen

Setze jetzt überall da wo in der Funktion ein $x$ steht ein $\infty$ bzw. $- \infty$ ein und schaue was raus kommt. Allerdings darfst du das nur in Anführungszeichen schreiben, da dies eigentlich keine mathematische Ausdrucksweise ist und somit nur eine inoffizielle Lösung aber eine gute Hilfe um sich das besser vorstellen zu können.

" f (\infty) = - 3 \cdot \infty^{4} - 2 \cdot \infty^{2} + 5 "

Schaue dir jetzt das Vorzeichen vor dem höchsten Exponenten/Grad an: hier steht ein Minus. Also kommt insgesamt Minus Unendlich raus.

\lim_{x \to \infty} f (x) = - \infty

" f (- \infty) = - 3 \cdot (- \infty)^{4} - 2 \cdot (- \infty)^{2} + 5 "

Bei geraden Exponenten wird das Minus in der Klammer wieder zu einem Plus und du kommst auf das selbe Ergebnis.

\lim_{x \to - \infty} f (x) = - \infty

Der Verlauf ist also "von unten nach unten".

4. Schritt: Symmetrie

Es können drei Fälle eintreten: Achsensymmetrie, Punktsymmetrie, keine Symmetrie. Ersetze dafür jedes $x$ mit einem $- x$ .

f (- x) = - 3 \cdot (- x)^{4} - 2 \cdot (- x)^{2} + 5

Jetzt musst du dir die Exponenten/Potenzen anschauen, hier sind das nur gerade, also fallen unsere Minuszeichen vor den $x$ weg. Damit bist du wieder bei der Funktion gelandet.

f (- x) = f (x)

Welche Symmetrie war das? Richtig, die Achsensymmetrie.

5. Schritt: y-Achsen Abschnitt

Um den Schnittpunkt einer Funktion mit der y-Achse zu ermitteln, muss für den $x$ -Wert $0$ eingesetzt werden.

6. Schritt: Graphen zeichnen

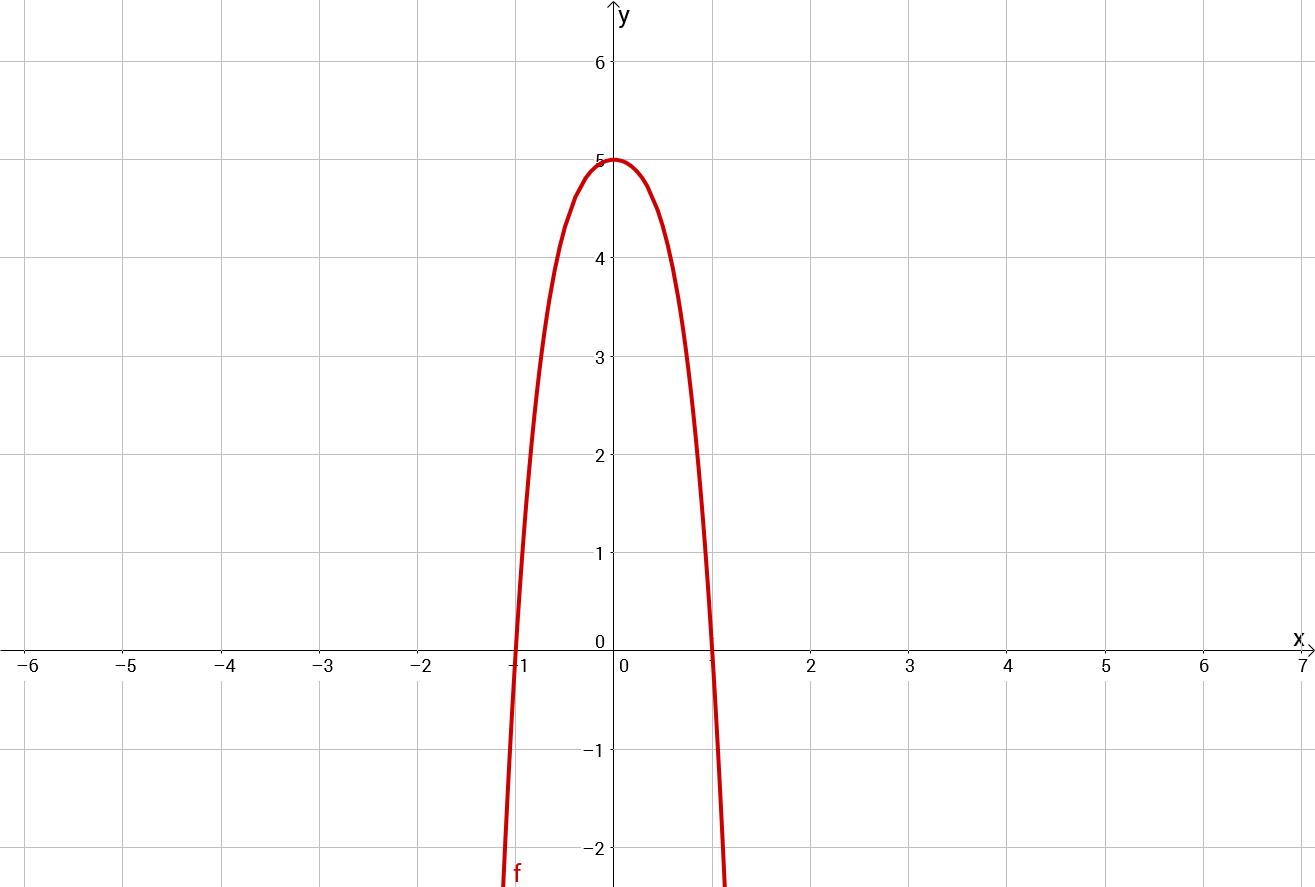
Lösung 2: durch Substitution

Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. $z$ ) ersetzt.

f (x) = - 3 x^{4} - 2 x^{2} + 5

Ersetze nun jedes $x^{2}$ mit $z$ .

f (z) = - 3 z^{2} - 2 z + 5

Aus dieser quadratischen Funktion kannst du jetzt die Nullstellen mit Hilfe der Mitternachtsformel ausrechnen.

$z_{1} = - \frac{5}{3}$ und $z_{2} = 1$

Nun musst du rücksubstituieren.

z_{1} = (x_{1})^{2}

z_{2} = (x_{2})^{2}

Um auf $x_{1}$ und $x_{2}$ zu kommen musst du also die Wurzel aus $z_{1}$ und $z_{2}$ ziehen. Das funktioniert allerdings nur bei $z_{2}$ , da $z_{1}$ negativ ist. Aber Achtung: Nur die Wurzel ziehen ist keine Äquivalenzumformung, deshalb musst du die $\pm \sqrt{z}$ ziehen.

x_{1} = 1

x_{2} = - 1

So bist du wieder bei den Nullstellen von oben angekommen und kannst bei Schritt 3: Verhalten im Unendlichen weiter machen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?