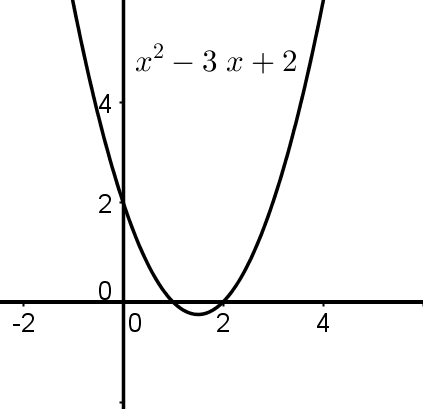
Nullstellen
Quadratische Funktionen sind Polynome zweiten Grades und haben deswegen höchstens zwei reelle Nullstellen.
Die Anzahl der Nullstellen wird durch die Diskriminante der Funktion angegeben:
Vorzeichen der Diskriminante | |||
|---|---|---|---|
Graph der Funktion (schematisch) | 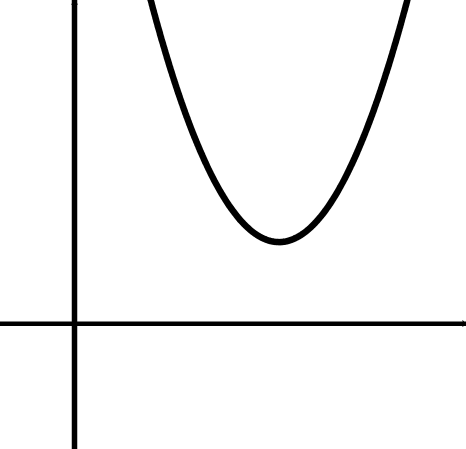 |  | 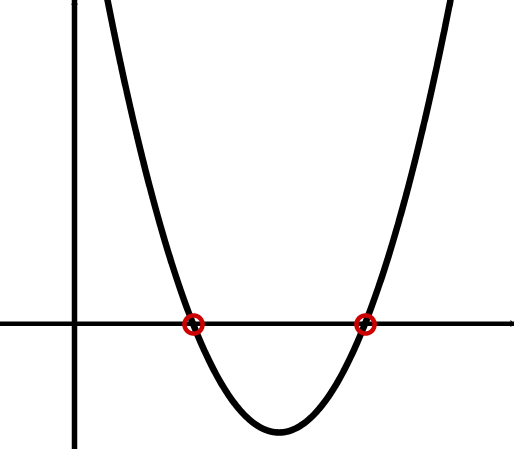 |
Anzahl der Nullstellen | keine Nullstelle | eine doppelte Nullstelle | zwei einfache Nullstellen |
Um die Lage der Nullstellen zu bestimmen, muss man eine quadratische Gleichung lösen, z.B. mithilfe der Mitternachtsformel, bei der die Funktion gleich gesetzt werden muss.
Scheitel
Als Scheitel einer Parabel bezeichnet man ihr Extremum. Es liegt immer bei .
Man erhält den Scheitelpunkt einer Parabel entweder durch quadratische Ergänzung oder wie bei allen Funktionen durch die erste Ableitung.
Setzt man den x-Wert wieder in die Gleichung der quadratischen Funktion ein, erhält man den Scheitelpunkt, dieser hat dann die Koordinaten:
Darstellungsformen einer quadratischen Funktion
Der Funktionsterm einer quadratischen Funktion kann - ggf. nach Umformung bzw. Zusammenfassung - vorliegen in:
Nullstellenform / Linearfaktorform: (nur möglich, falls f Nullstellen hat)
Bedeutung der Koeffizienten einer quadratischen Funktion
Eine quadratische Funktion hat in allgemeiner Form eine Gleichung der Form .
Die Koeffizienten und verformen und / oder verschieben die Parabel. Welchen genauen Einfluss sie auf die Form des Graphen haben, kann aber nur anhand der Scheitelform gesehen werden.
Vergleiche dazu den Artikel Einfluss der Parameter in der Scheitelform.
Video zur Scheitelform
Laden
Übungsaufgaben
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: