Aufgaben zur Hinführung auf schwierige Extremwertprobleme

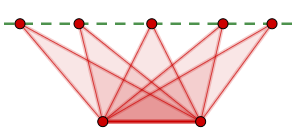
Manche ebene geometrische Figuren werden alleine durch ihren Umfang oder alleine durch ihren Flächeninhalt bestimmt.

Einige ebene geometrische Formen sind umfangsstabil. Das heißt, flächengleiche Figuren solch einer Form haben auch gleichen Umfang.

Welche der folgenden Aussagen stimmt?
Klicke die Zutreffenden an!
- Je größer der Flächeninhalt eines Kreises, desto größer sein Umfang.
- Je größer der Flächeninhalt eines Quadrats, desto größer sein Umfang.
- Je größer der Flächeninhalt eines Dreiecks, desto größer sein Umfang.
Bei dieser Aufgabe geht es um den Zusammenhang von Umfang und Flächeninhalt bei Kreisen, bei Dreiecken und bei Quadraten.
Quadrate sind umfangsstabil:
Je größer der Umfang eines Quadrats, desto größer sein Flächeninhalt.
Genauer gilt mit der Quadratseite $a$ :
$\displaystyle U_{Q} =4\cdot a\quad \Rightarrow\quad a=\frac{U_{Q}}{4}\quad$ und somit:
$\displaystyle A_{Quadrat} = a^2\;=\left(\frac {U_{Q}}{4}\right)^2=\frac {1} {16}\cdot \left(U_{Q}\right) ^2$
Kreise sind umfangsstabil:
Je größer der Umfang eines Kreises, desto größer sein Flächeninhalt.
Genauer gilt mit dem Radius $r$ :
$\displaystyle U_{r}= 2r\pi\quad\Rightarrow\quad r= \frac {U_{r}}{2\pi}\quad$ und somit:
$\displaystyle A_{Kreis}= r^2\cdot \pi=\frac{1}{4\pi}\cdot\left(U_{r}\right)^2$
Dreiecke sind nicht umfangsstabil:
Vergleiche die Dreiecke in der nebenstehenden Grafik:
Wegen gleicher Grundlinie und gleicher Höhe haben alle fünf Dreiecke gleiche Fläche aber unterschiedliche Umfänge.
Ergänzung:
Gleichseitige Dreiecke sind umfangsgleiche geometrische Formen:
Bei gegebener Dreieckseite $a$ gilt:
$\displaystyle U_{gl.s.Dr.}=3\cdot a\quad \Rightarrow\quad a=\frac{U_{gl.s.Dr.}}{3}\quad$ und somit:
$\displaystyle A_{gl.s.Dr.}=\frac{\sqrt{3}}{4}\cdot a^2=\frac{\sqrt{3}}{36}\cdot \left(U_{gl.s.Dr.}\right)^2$
Ein vorgegebener Umfang bestimmt also den Flächeninhalt eines gleichseitigen Dreiecks eindeutig.
Die Behauptung "Je größer der Umfang eines Dreiecks, desto größer sein Flächeninhalt" gilt demnach nur für gleichseitige Dreiecke.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

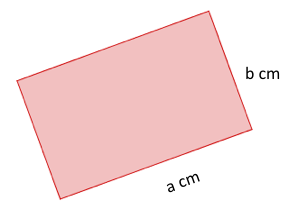
Zeige, dass ein Rechteck nicht formstabil ist:

Erzeuge zur Begründung im nebenstehenden Applet durch Verschieben des Reglers 5 weitere Rechtecke.

Worin stimmen alle 6 Rechtecke überein?

Worin unterscheiden sie sich?

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/e9wz6bpv]

Bei dieser Aufgabe entdeckst du, dass Rechtecke bei gleichem Umfang unterschiedliche Flächeninhalte haben können.

Die Maße der Rechtecke:

	a	b	Umfang	Fläche
Rechteck 1	0,3 LE	1,7 LE	4 LE	0,51 LE²
Rechteck 2	0,6 LE	1,4 LE	4 LE	0,84 LE²
Rechteck 3	0,9 LE	1,1 LE	4 LE	0,99 LE²
Rechteck 4	1,2 LE	0,8 LE	4 LE	0,96 LE²
Rechteck 5	1,5 LE	0,5 LE	4 LE	0,73 LE²
Rechteck 6	1,8 LE	0,2 LE	4 LE	0,36 LE²

Ergebnis:

Alle Rechtecke haben gleichen Umfang, aber unterschiedliche Flächeninhalte.

Dazu könnte man auch sagen, Rechtecke sind nicht formstabil.

Naheliegend ist dadurch die Überlegung:

Welche Rechtecksform liefert bei einem Rechtecksumfang von $4\,\text{LE}$ die größte Fläche?

Diese Extremwertaufgabe löst du in der nächsten Aufgabe.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

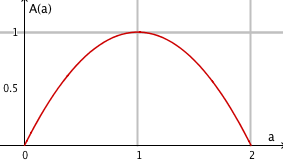
Ein Rechteck habe den Umfang $U=4\,\text{cm}$ . Berechne die Seitenlängen $a$ und $b$ so, dass das Rechteck den größtmöglichen Flächeninhalt $A$ besitzt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

In dieser Aufgabe bestimmst du das größtmögliche Rechteck durch die Ableitung oder alternativ durch die quadratische Ergänzung der Zielfunktion.

Der Umfang $U$ des Rechtecks beträgt $4\,\text{cm}$ bei den noch nicht bekannten Seitenlängen $a\,\text{cm}$ und $b\,\text{cm}$ .

Gesucht ist der größtmögliche Flächeninhalt $A$ des Rechtecks.

Die Formel für den Flächeninhalt eines Rechtecks ergibt deshalb die Zielfunktion.

Hinweis:

Haben bei Extremwertaufgaben die betrachteten Größen die gleiche Maßeinheit, begnügt man sich bei den verwendeten Funktionen meist auf die Angaben der jeweiligen Maßzahlen.

Zielfunktion:

$A(a;b)=a\cdot b$

Die Formel für den vorgegebenen Umfang ist die Nebenbedingung der Extremwertaufgabe

Nebenbedingung:

$U(a;b)=2\cdot a + 2\cdot b$

Setze in die Nebenbedingung für $U(a;b)$ den Wert 4 ein.

$2a+2b=4$

Löse die Gleichung nach $b$ auf. (Du könntest auch nach $a$ auflösen.)

$\Rightarrow\quad\; b=2-a$

Setze in der Zielfunktion für $b$ den Term $2-a$ an.

Beachte: $A$ wird dadurch zu einer Funktion der einen Varaiablen $a$ .

\displaystyle A\left(a\right)

=

\displaystyle a\cdot\left(2-a\right)

↓

Multipliziere die Klammer aus.

Für $a$ gilt: $a\in\,]0;2[$ .

\displaystyle A\left(a\right)

=

\displaystyle -a^2+2a

$\mathbb {D}_A=\;]0;2[$

Bilde die 1. Ableitung der Zielfunktion $A(a)$ .

$A'(a)=-2a+2$

Setze $A'(a)$ gleich Null und löse nach $a$ auf.

$\def\arraystretch{1.25} \begin{array}{rcl}-2a+2&=0\\a&=1\end{array}$

Überprüfe mit der 2. Ableitung, dass $a=1$ tatsächlich für die Zielfunktion ein Maximum ergibt.

$A''(a)=-2$

$A''(a)$ ist eine konstante Funktion. Somit ist auch $A''(1)=-2< 0$ und $a=1$ ergibt einen maximalen Flächeninhalt.

Setze $a=1$ in die Nebenbedingung ein, um auch die 2. Rechtecksseite $b$ zu erhalten.

$b=2-1=1$

Ergebnis:

Das Rechteck, das bei einem gegebenen Umfang von 4 $\,\text{cm}$ den größtmöglichen Flächeninhalt besitzt, ist ein Quadrat mit der Seitenlänge 1 $\,\text{cm}$ . Der gesuchte Flächeninhalt ist also $1\,\text{cm}^2$ .

Alternative Lösung

Der Graph der Zielfunktion $A(a)=-a^2+2a;\quad \mathbb{D}_A=]0;2[$ ist eine nach unten geöffnete Parabel. Ihr Maximum ist der Scheitelpunkt.

Diesen kann man durch eine quadratische Ergänzung ermitteln.

$\displaystyle A$	$=$	$\displaystyle -a^2+2a$
	↓	Klammere $-1$ aus.
	$=$	$\displaystyle -\left(a^2-2a\right)$
	↓	Ergänze quadratisch.
	$=$	$\displaystyle -(a^2-2a\color{red}{+1^2}\color{green}{-1^2})$
	↓	Fasse zur binomischen Formel zusammen.
	$=$	$\displaystyle -\left(a-1\right)^2+1$

Lies nun den Scheitelpunkt ab.

$\Rightarrow\quad S(1|1)$

Aus der Zielfunktion für $a=1$ kannst du den maximalen Flächeninhalt bestimmen.

$\Rightarrow \quad A_{max}=A(1)=-1^2+2\cdot 1= 1$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇