Aufgaben zur allgemeinen Sinusfunktion
- 1
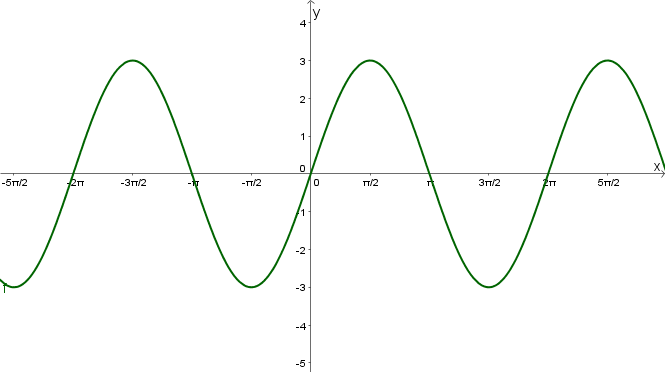
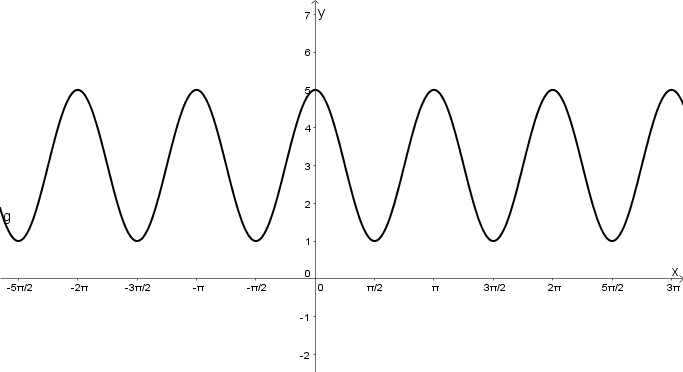
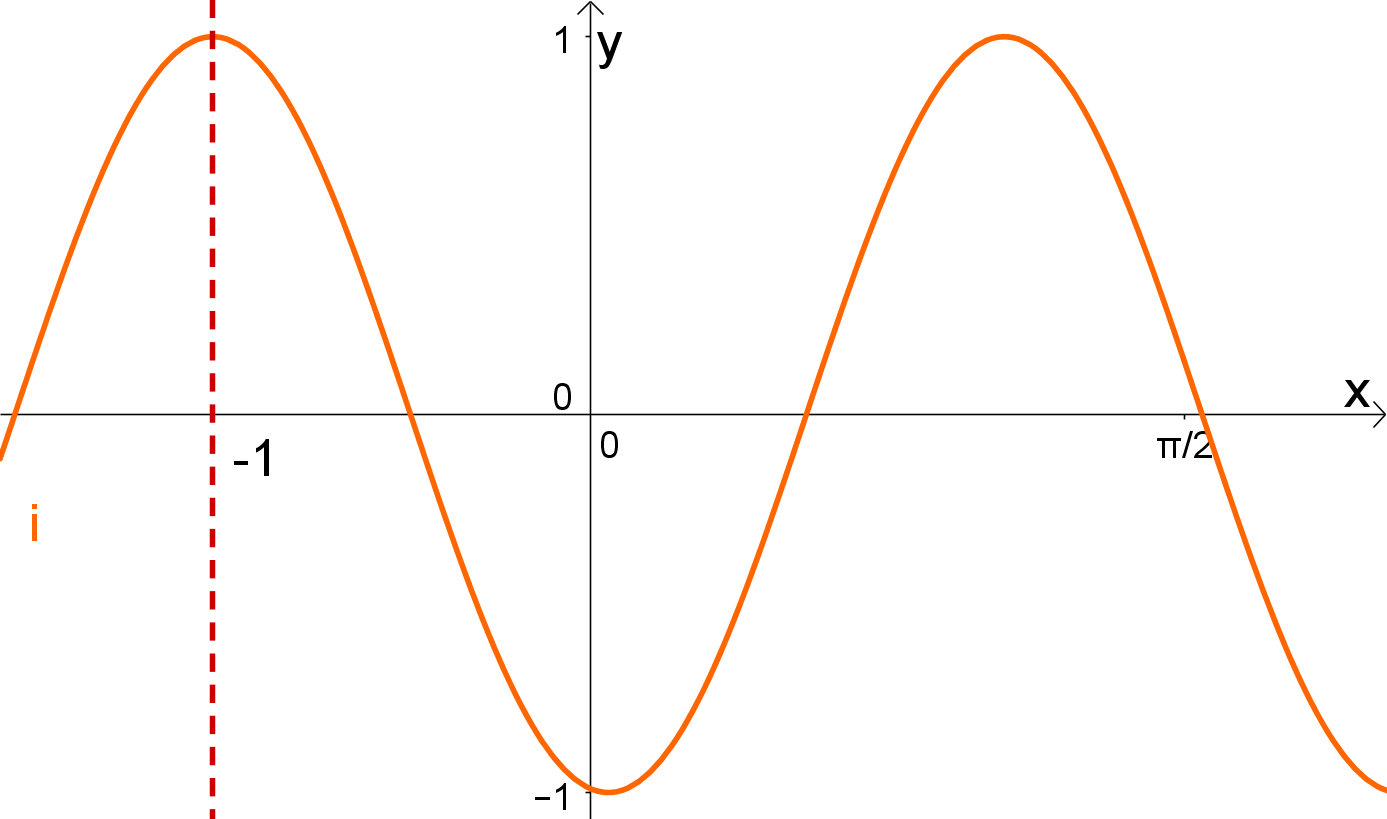
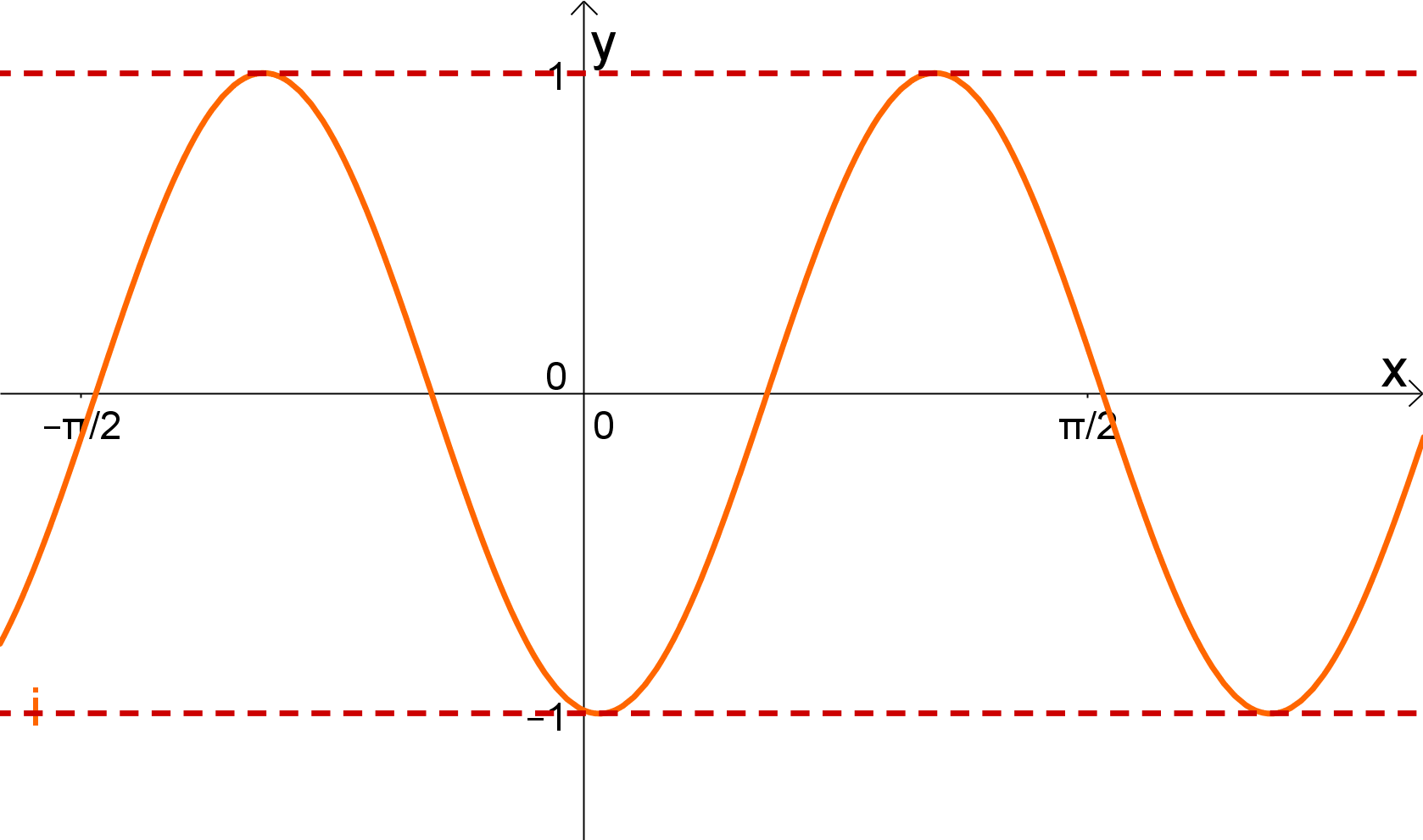
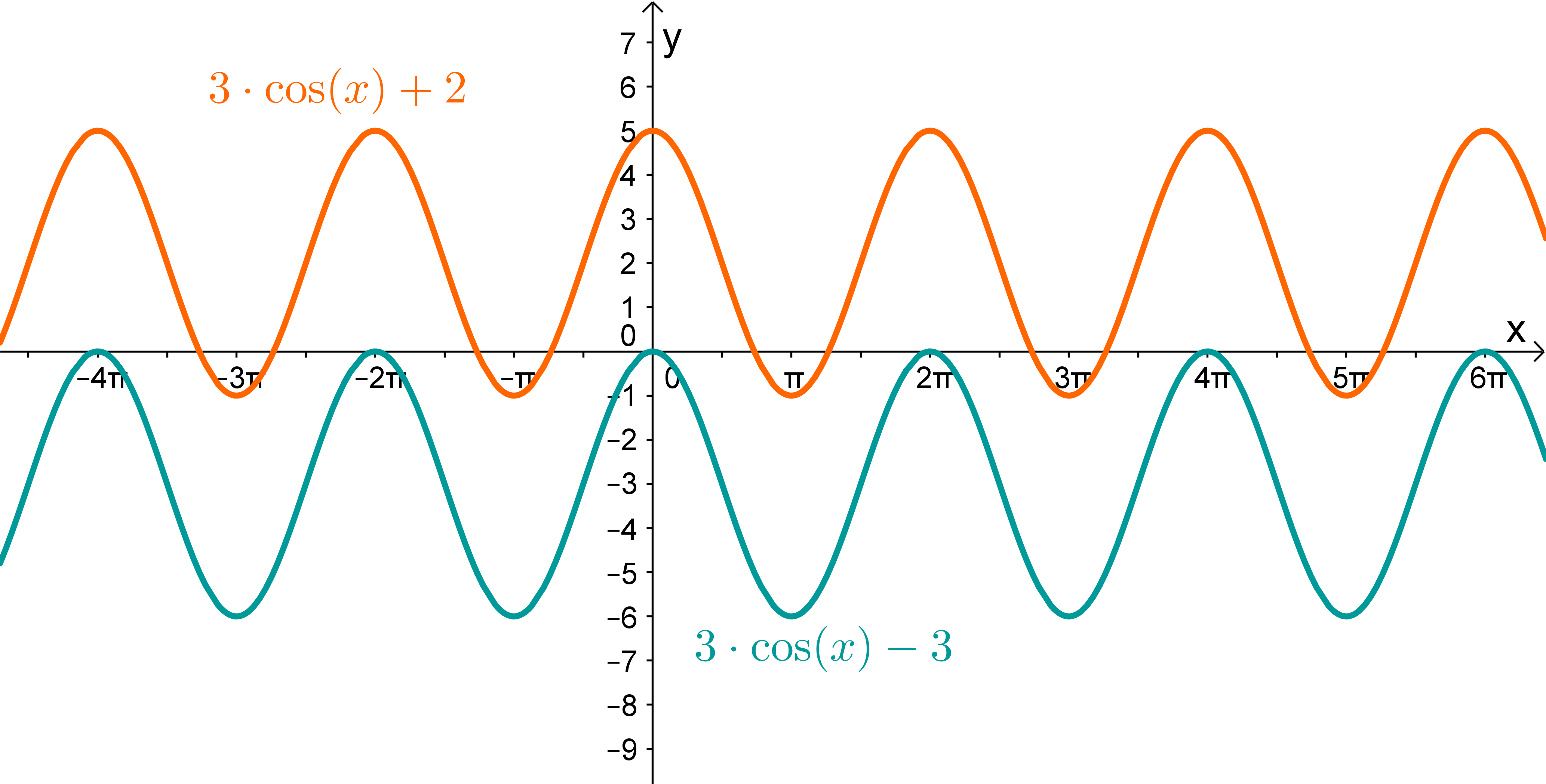
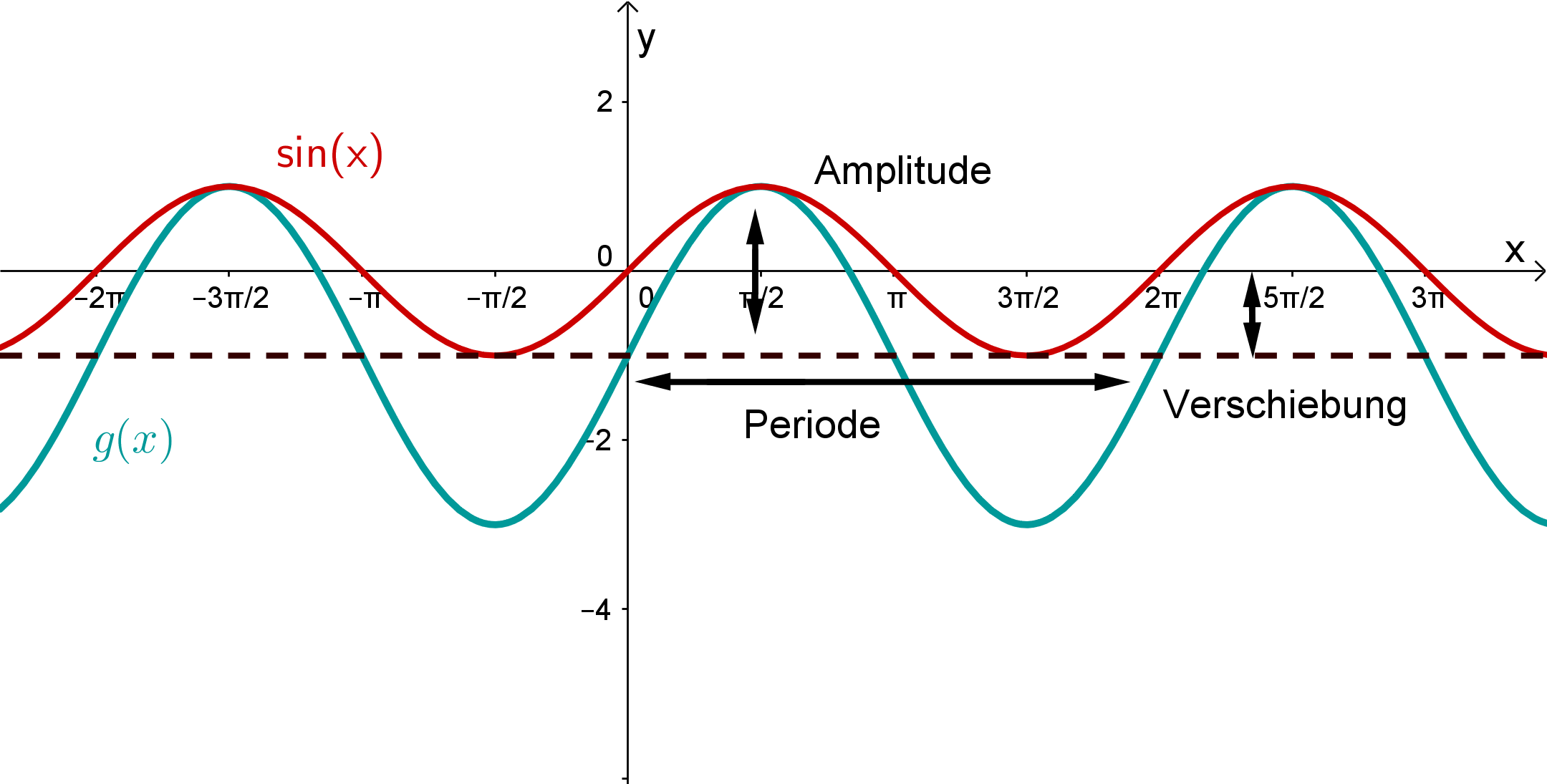
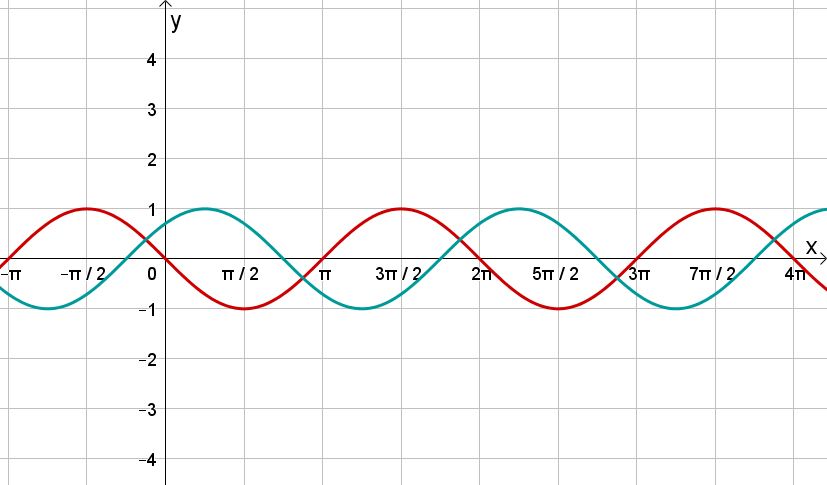
Finde die passenden Gleichungen zu den Funktionsgraphen:
- 2
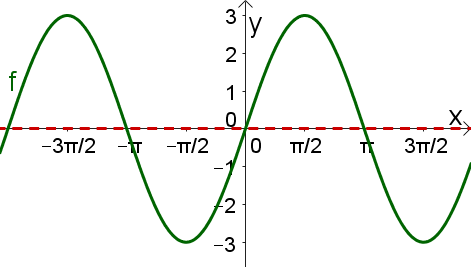
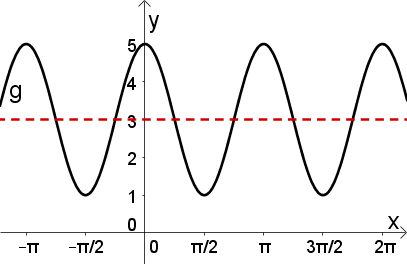
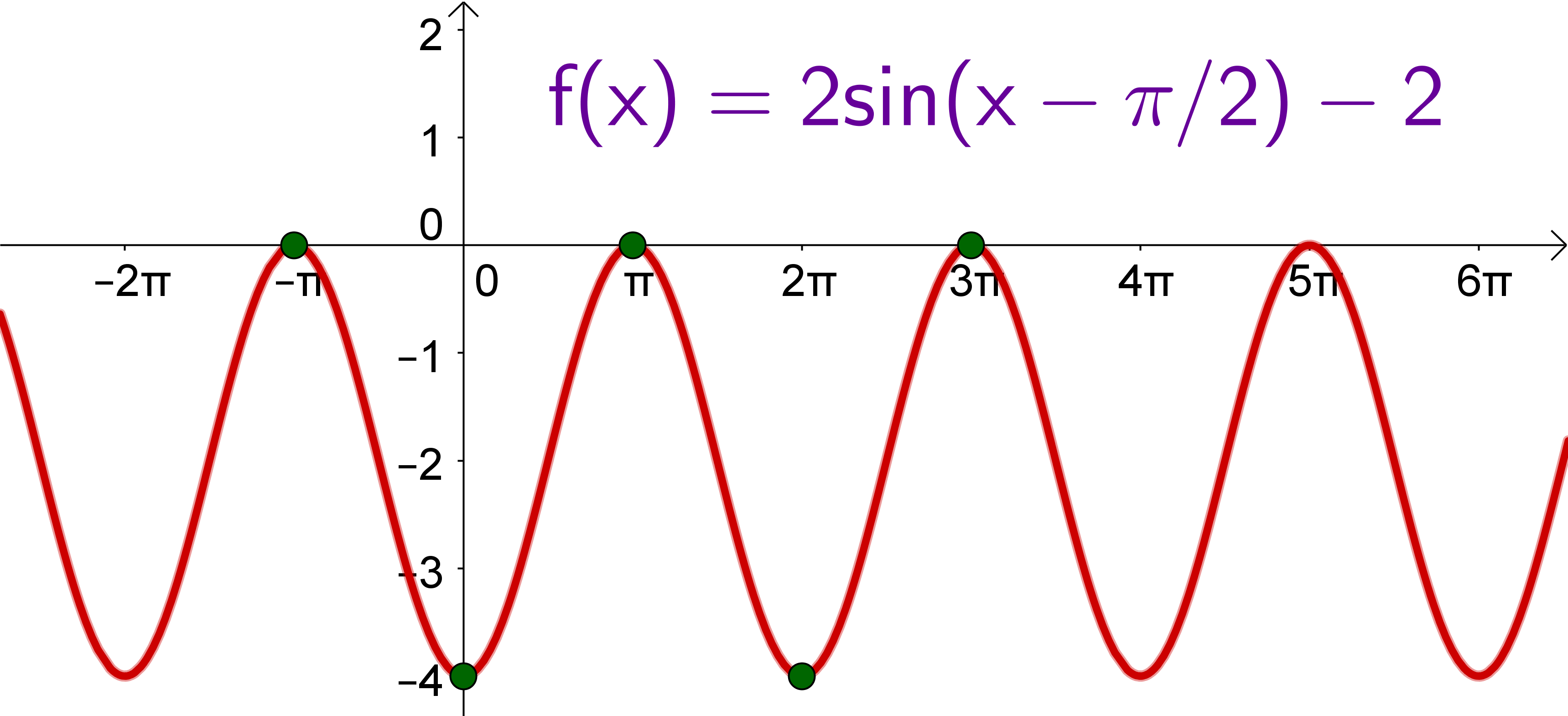
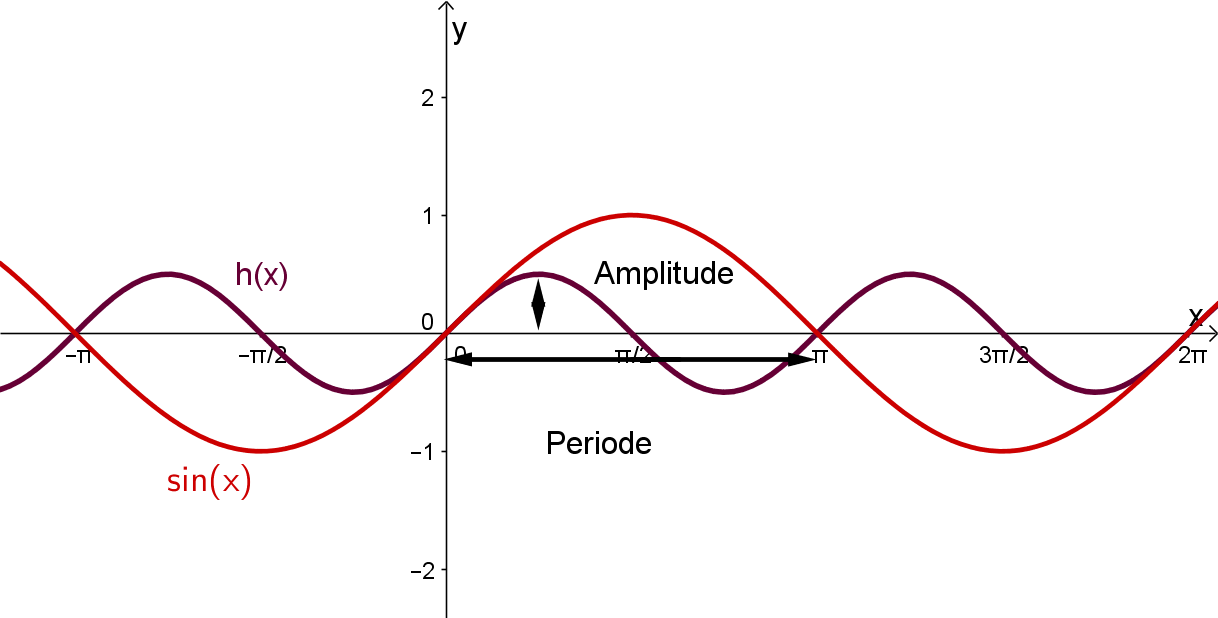
Ordne folgendem Graphen die richtige Funktionsgleichung zu:
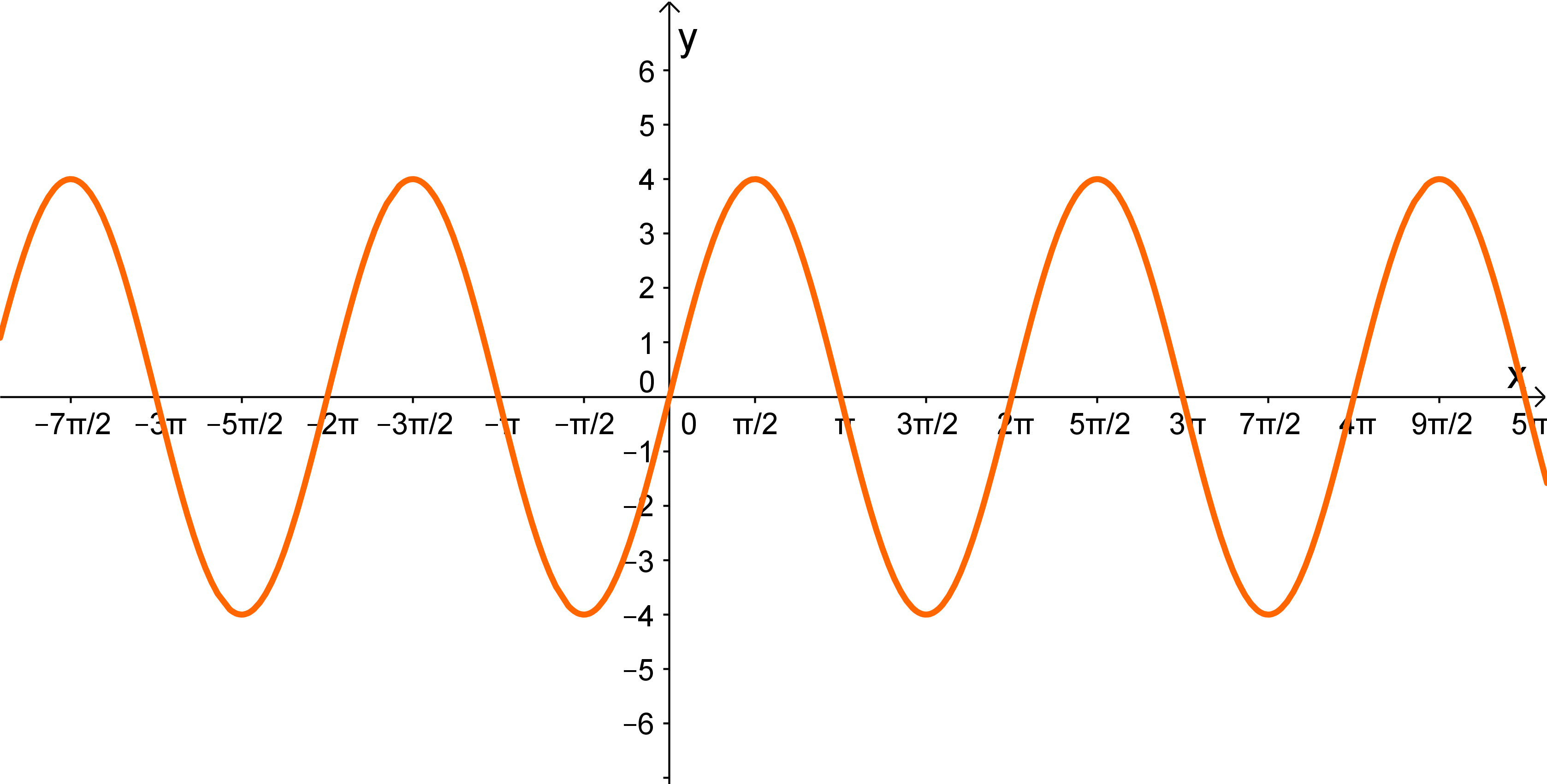
- 3
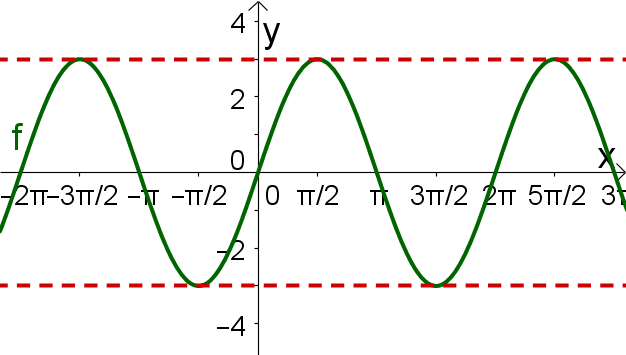
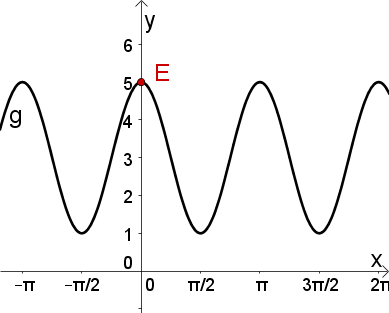
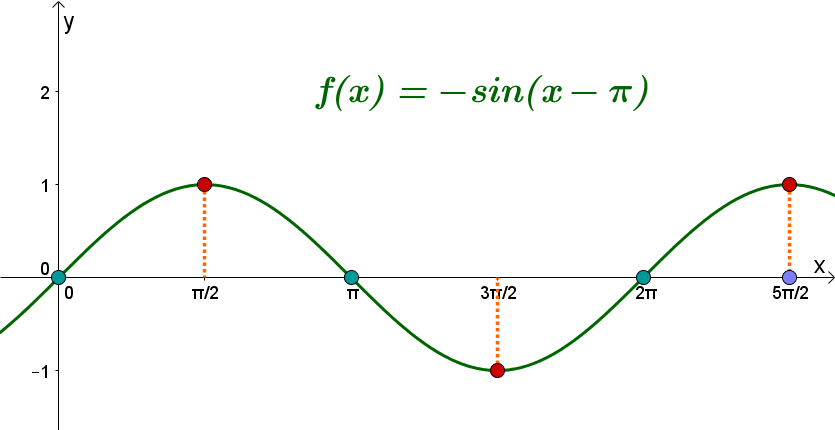
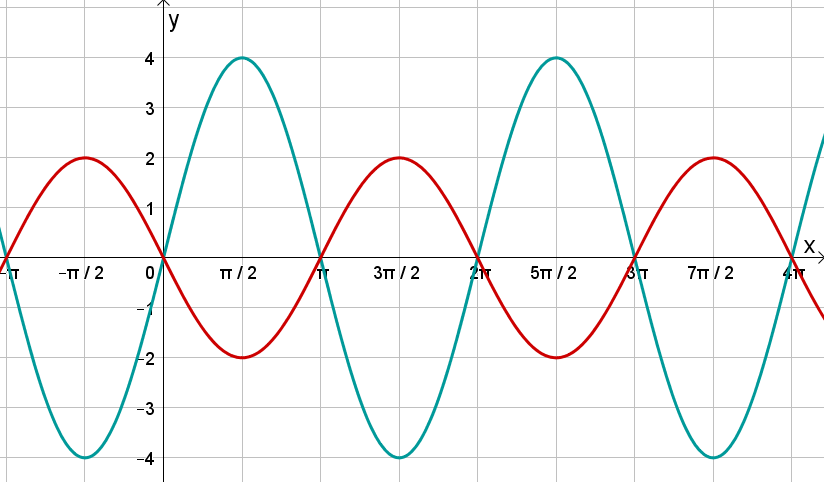
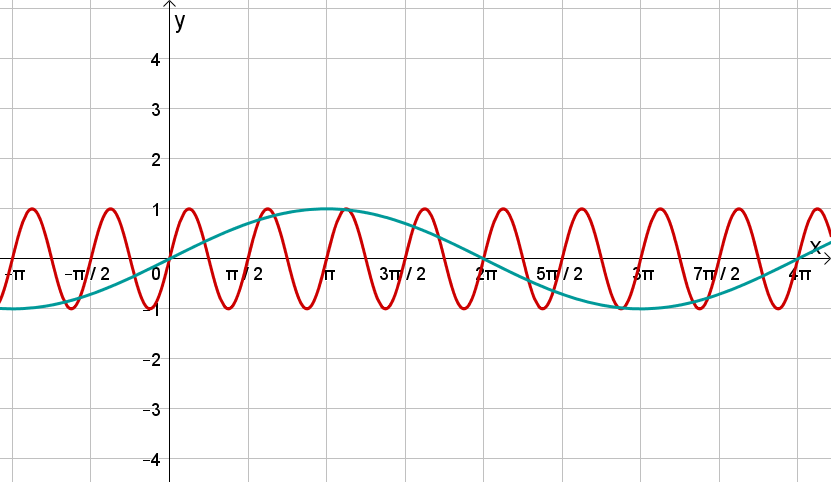
Ordne folgendem Graphen die richtige Funktionsgleichung zu:
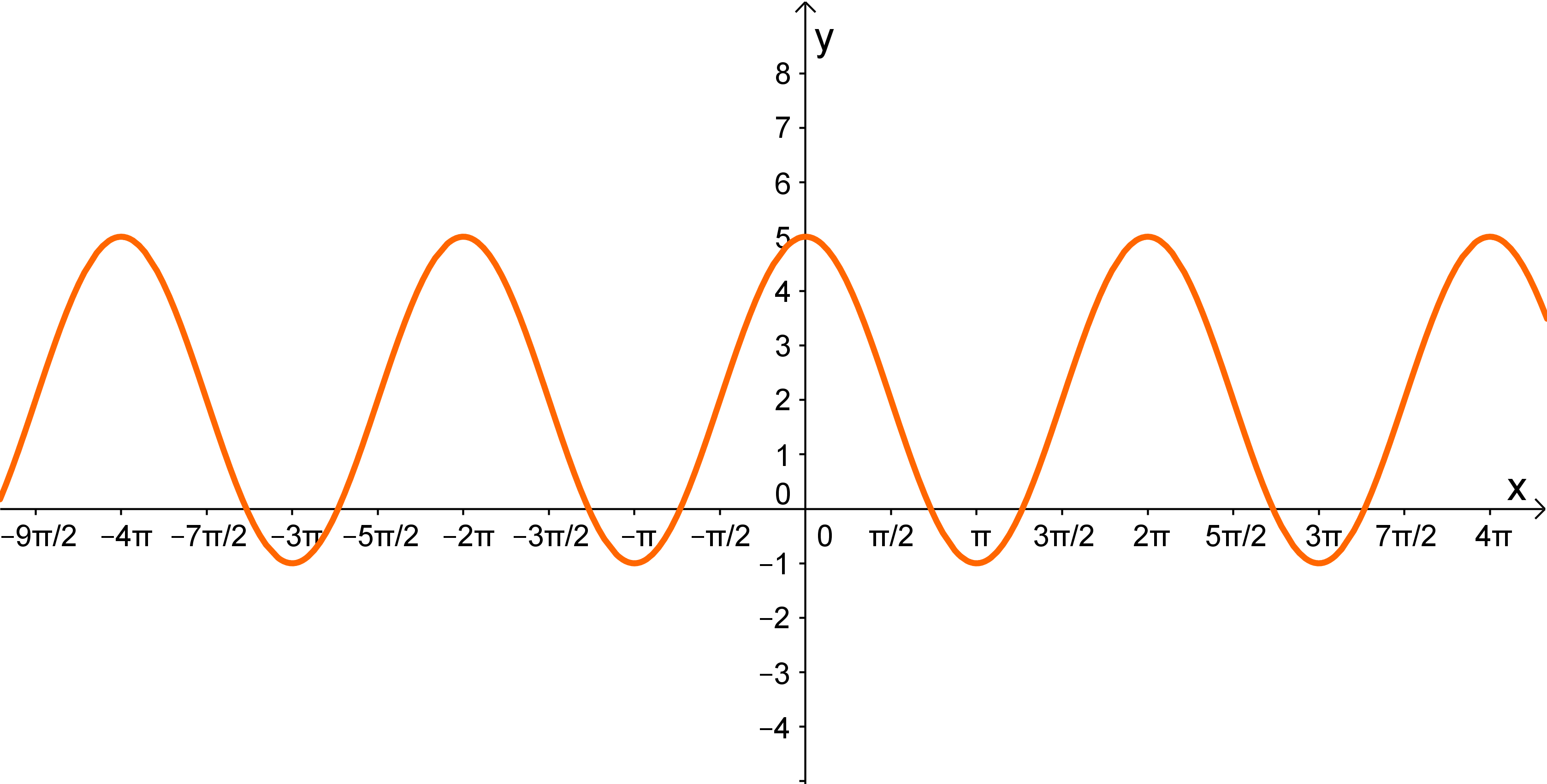
- 4
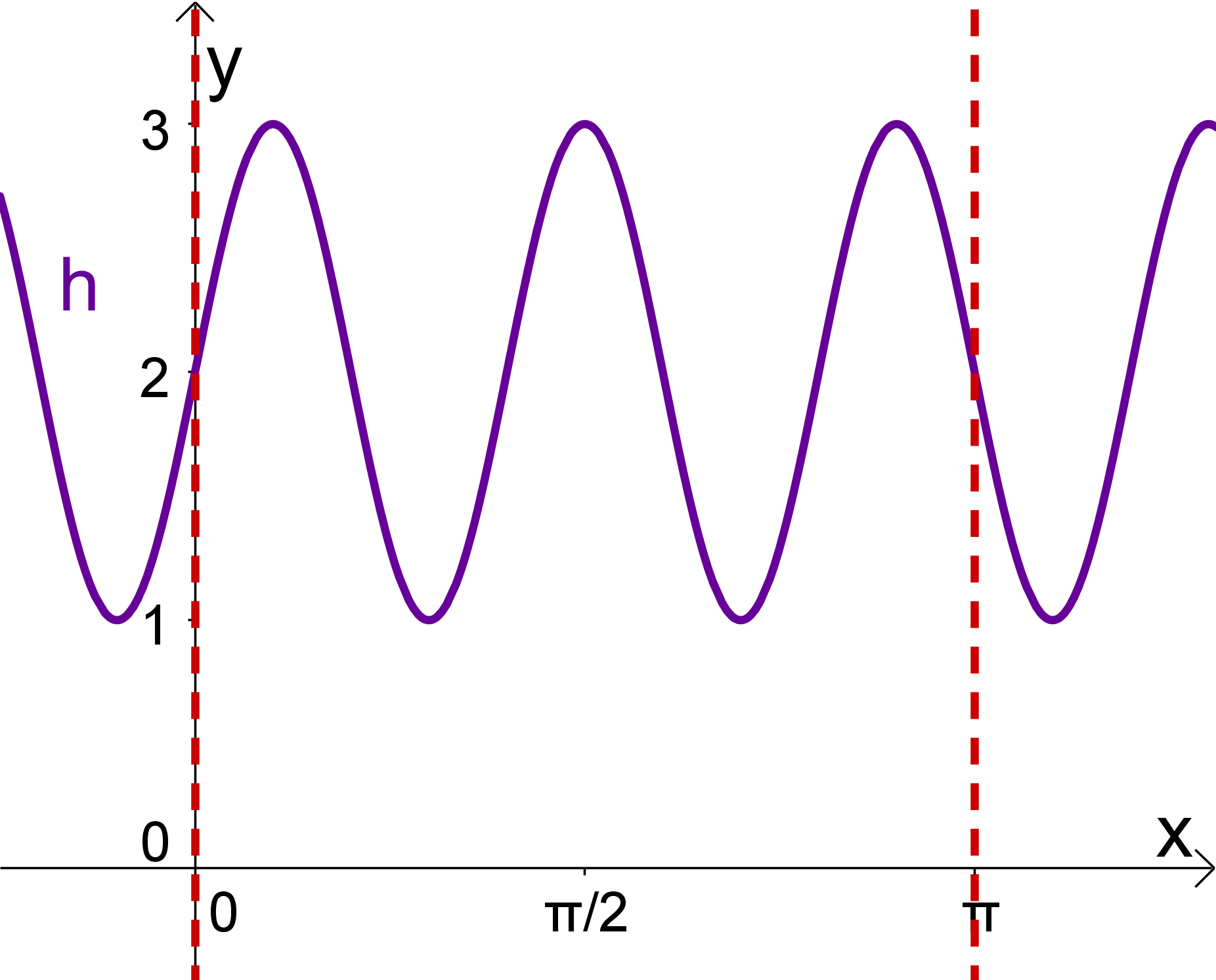
Zeichne die Funktion mit der Gleichung in ein Koordinatensystem.
- 5
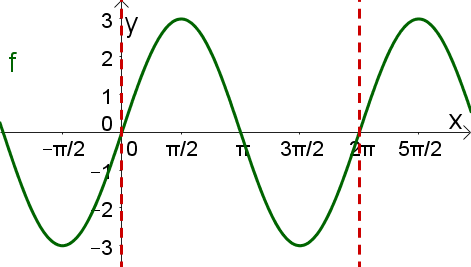
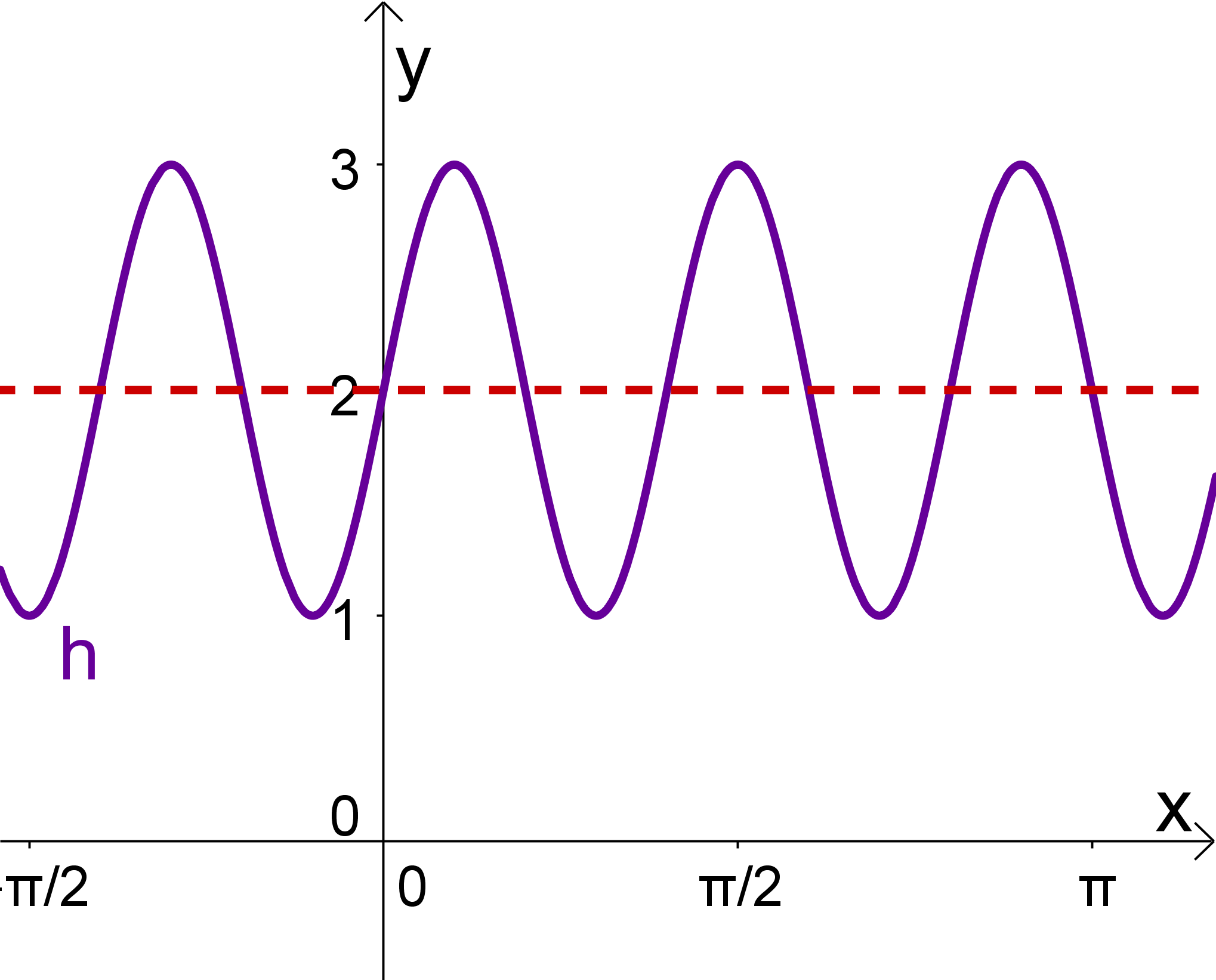
Zeichne im Definitionsbereich die manipulierte Sinusfunktion und lies ihren Wertebereich, Nullstellen und Extremstelle ab.
- 6
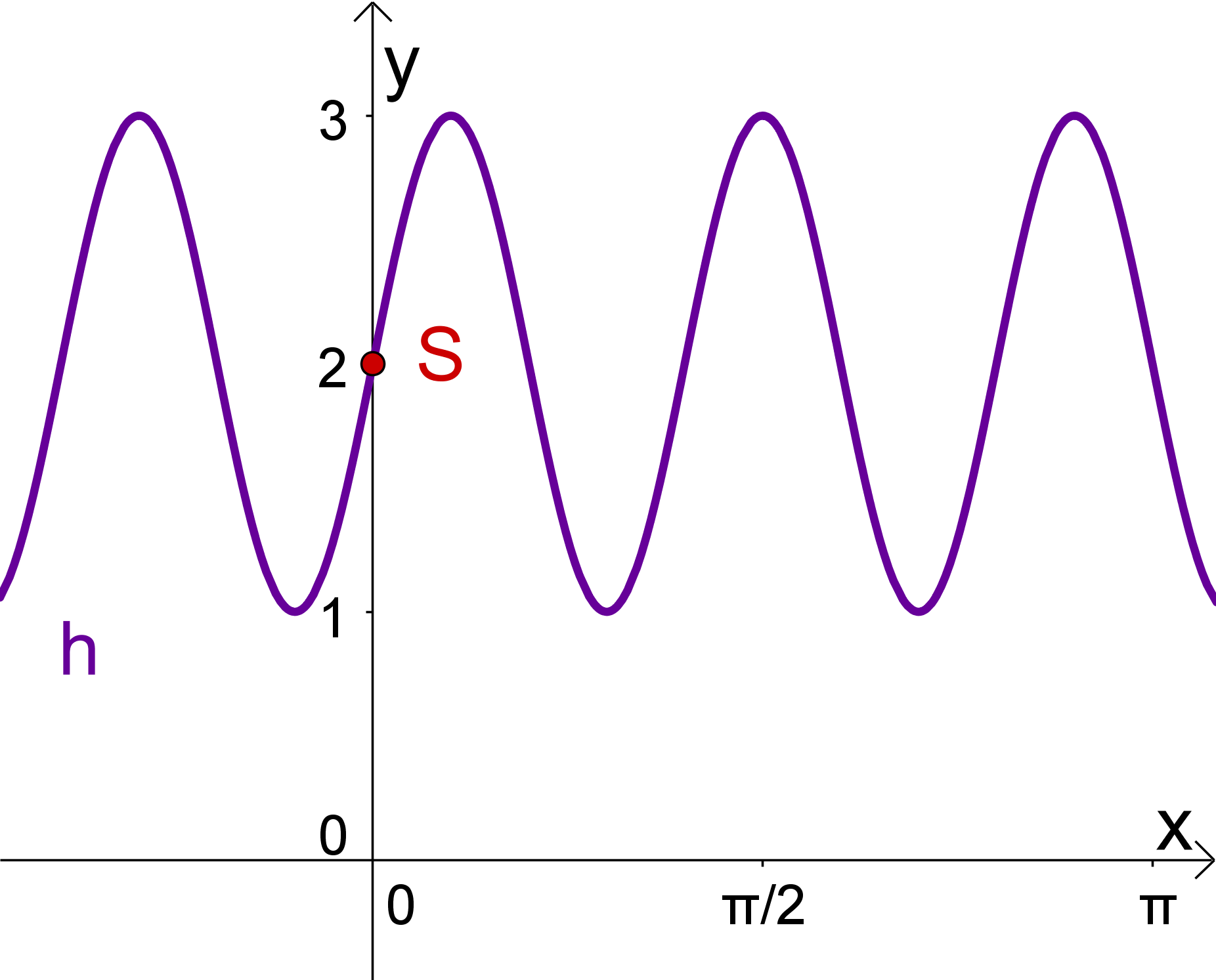
Zeichne im Definitionsbereich die manipulierte Sinusfunktion und lies ihren Wertebereich, Nullstellen und Extremstelle ab.
- 7
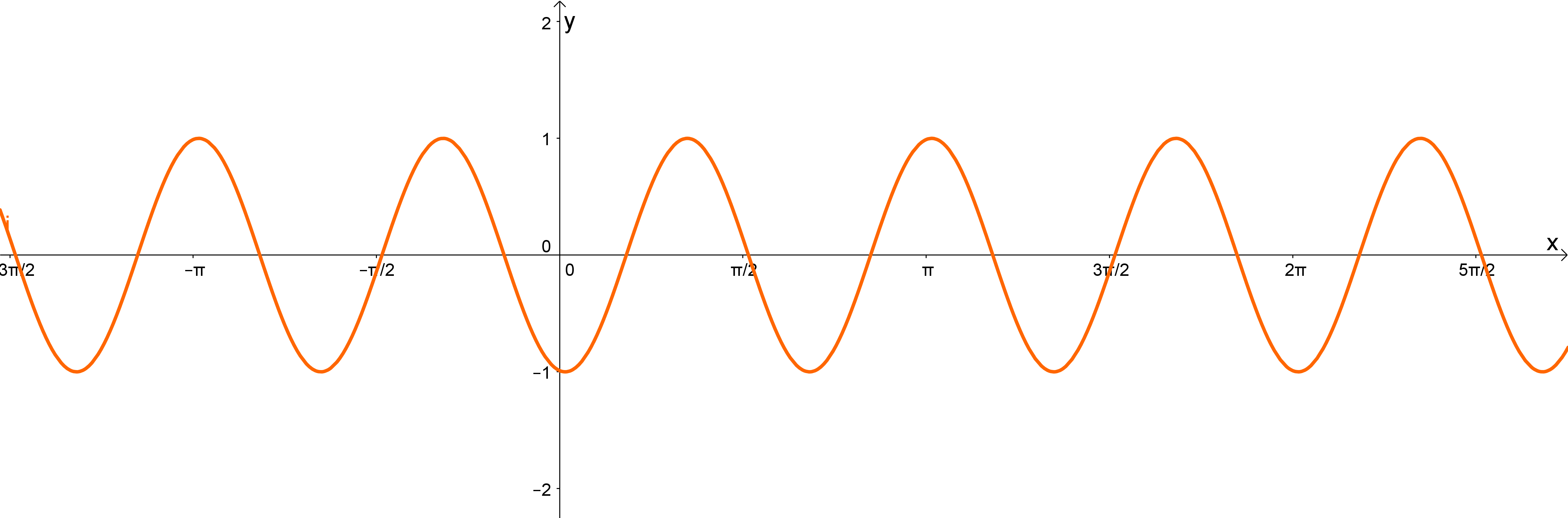
Notiere eine Wertetabelle, zeichne den Graphen und beobachte, wie sich jeweils der Graph im Vergleich zur Funktonsgleichung ändert.
. Formuliere: " " bewirkt…
. Formuliere: " " beim -Wert bewirkt…
. Formuliere: " " bewirkt…
. Formuliere: " " beim -Wert bewirkt…
- 8
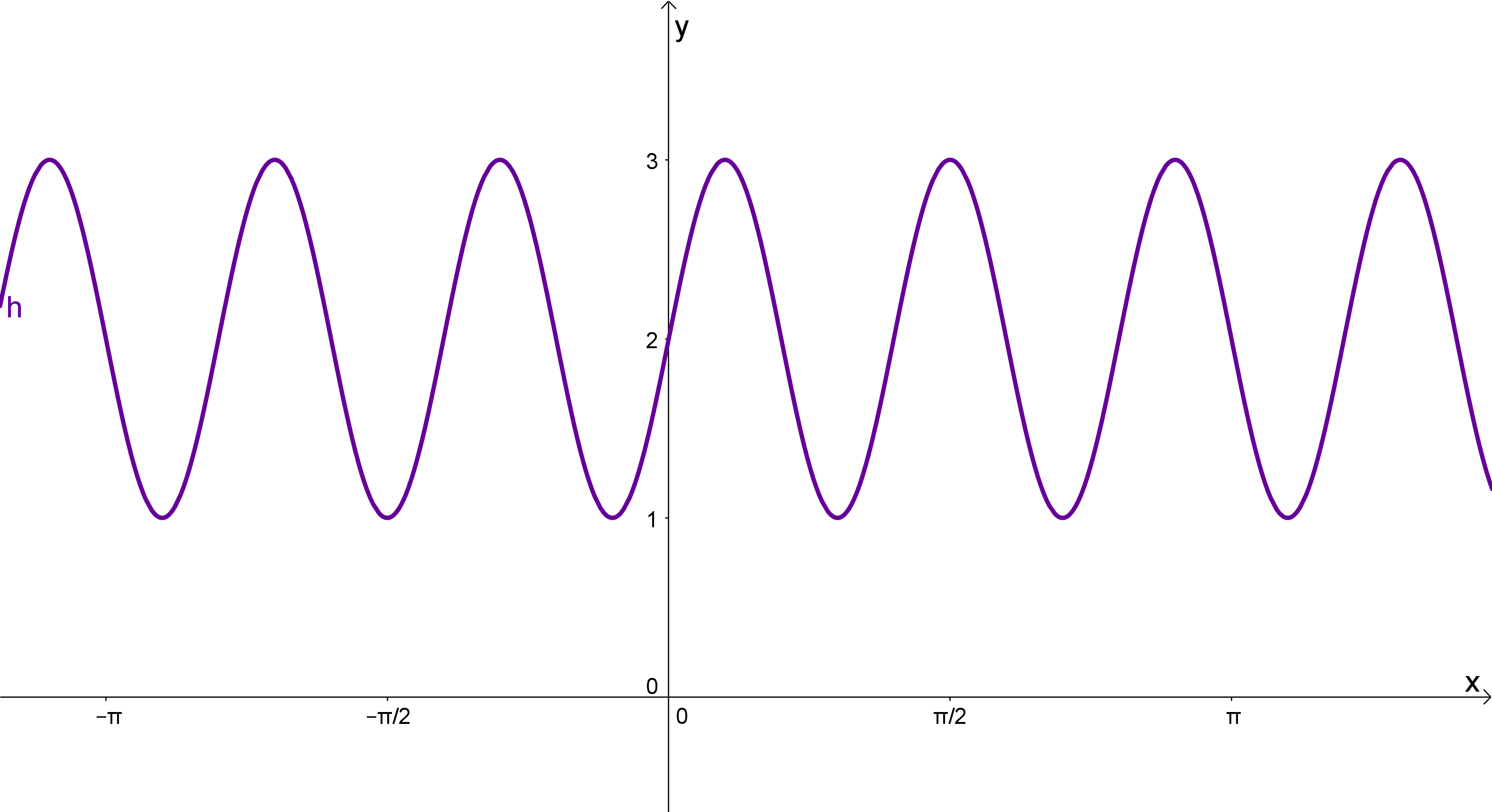
Bestimme die Funktionsgleichung zu folgenden Graphen:
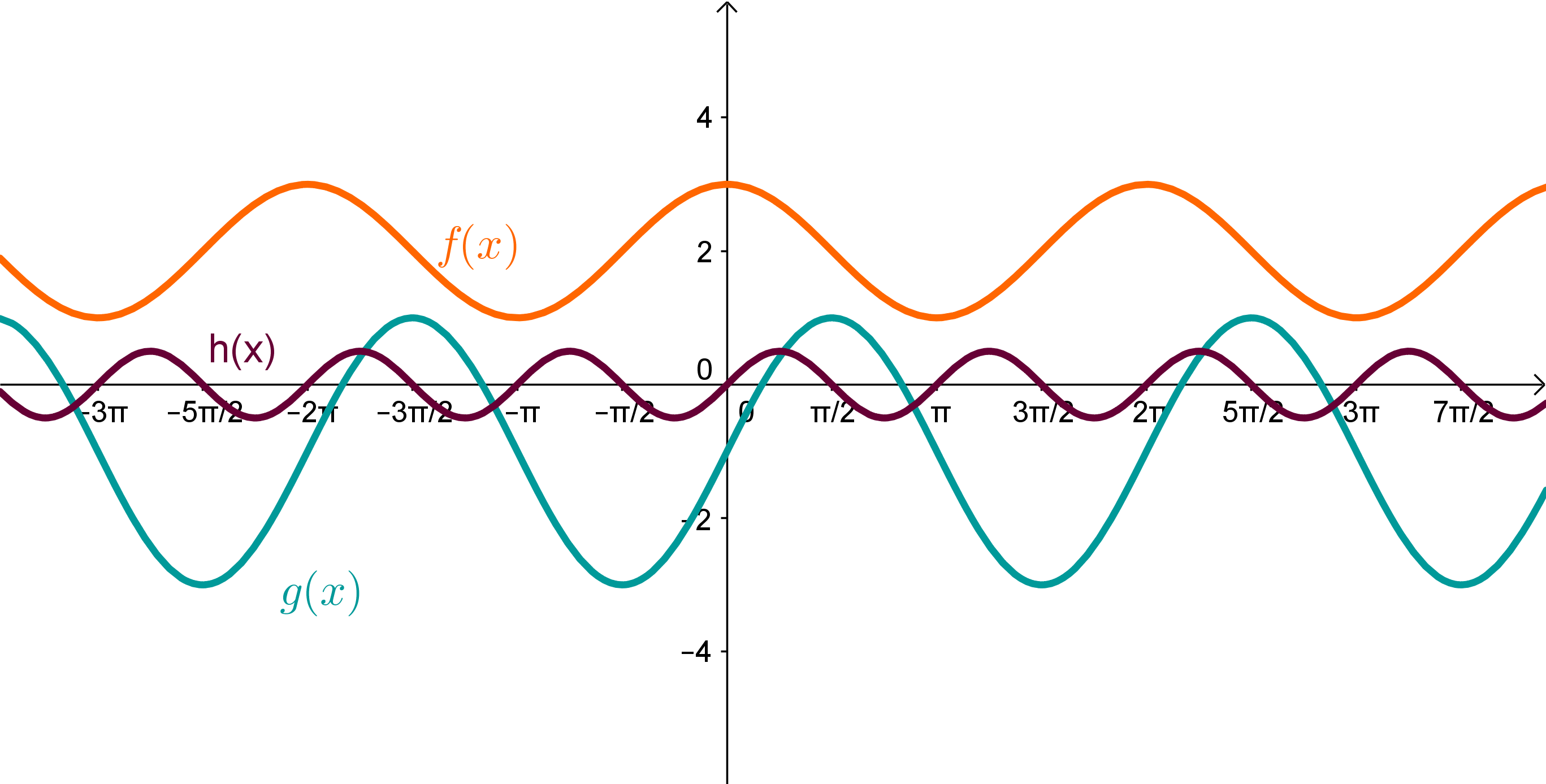
- 9
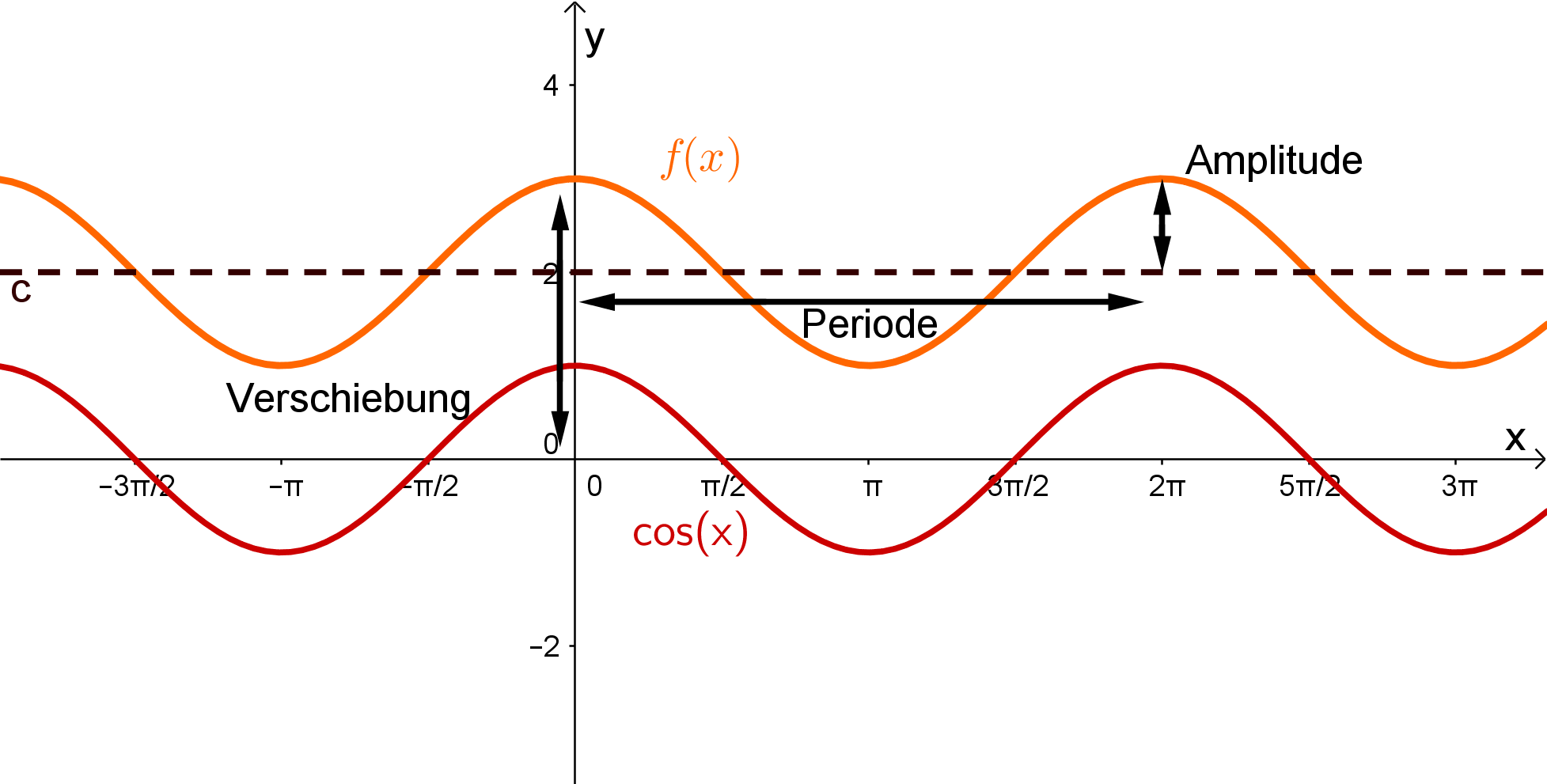
Verändere den Parameter und beobachte, wie sich der Funktionsgraph von , , gegenüber dem Graphen von (hier in schwarz abgebildet) ändert!
Beantworte anschließend die Fragen.
Für
Für
Für
Für
Für
Für
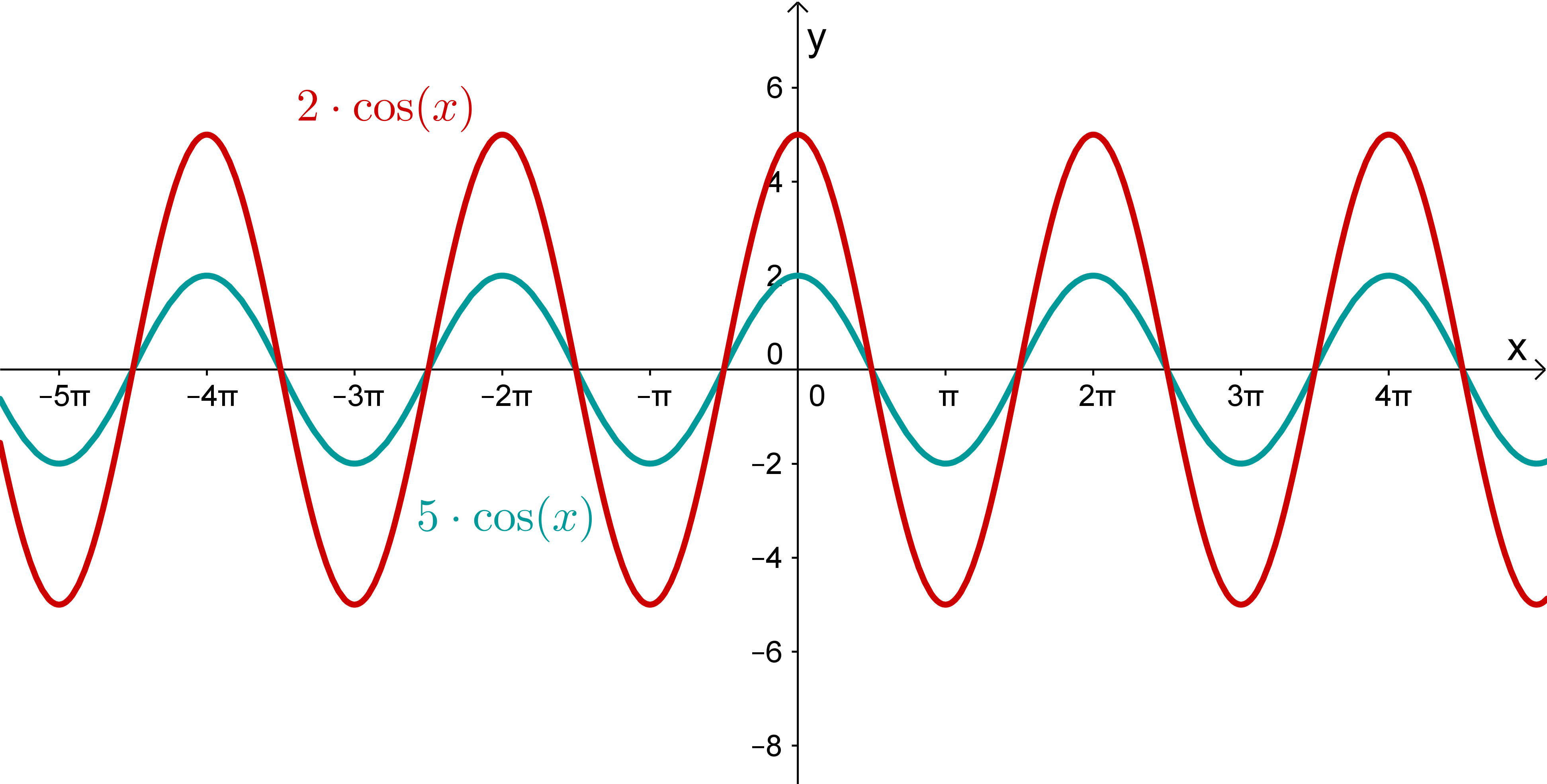
Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
- 10
Verändere den Parameter und beobachte, wie sich der Funktionsgraph von , , , gegenüber dem Graphen von (hier in grau abgebildet) ändert!
Beantworte anschließend die Fragen.
Für
Für
Für
Die Periode der Funktion mit der Funktionsgleichung ,
Die Periode der Funktion mit der Funktionsgleichung ,
Die Periode der Funktion mit der Funktionsgleichung ,
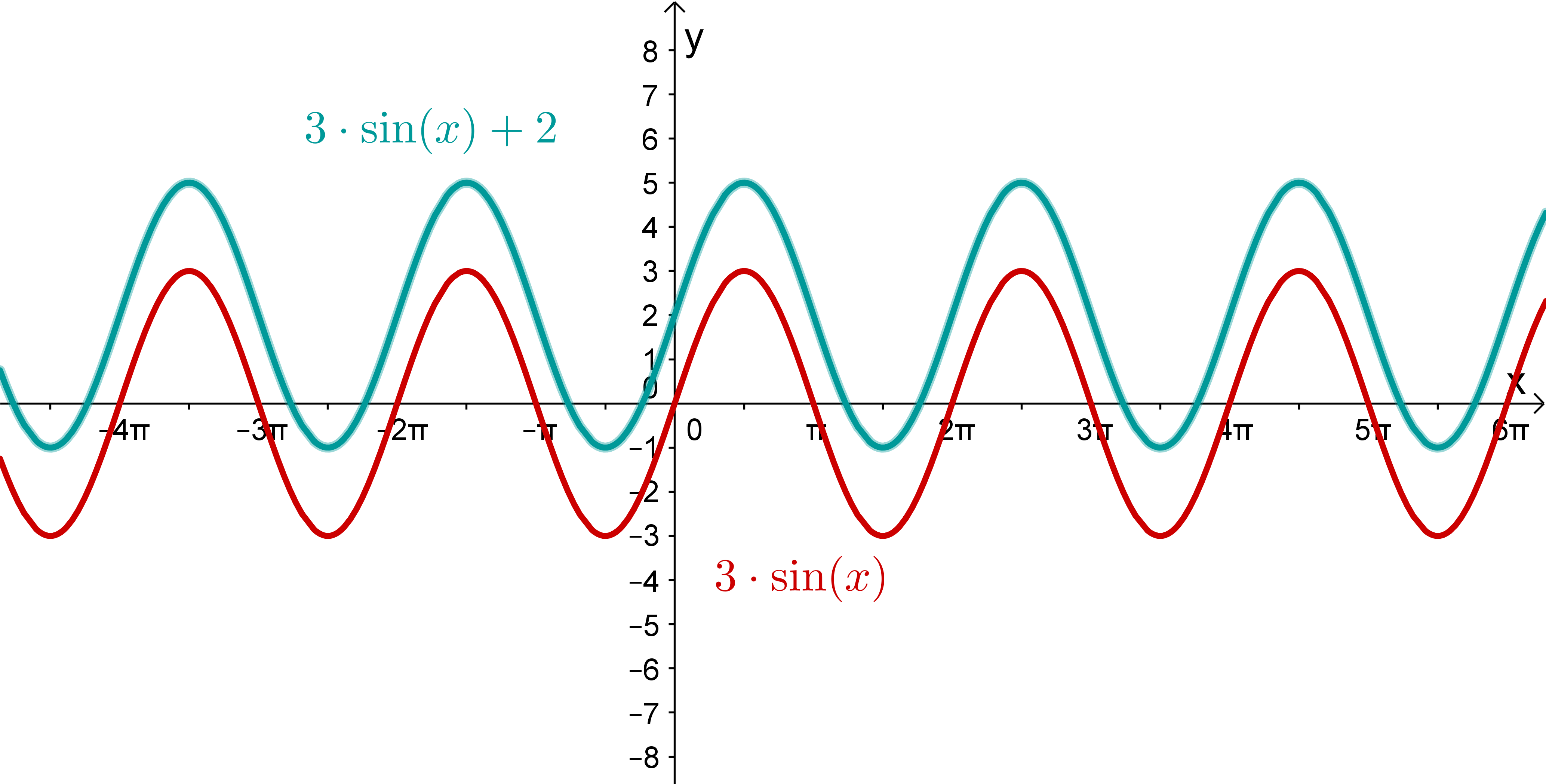
Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
- 11
Verändere den Parameter und beobachte, wie sich der Funktionsgraph von , , gegenüber dem Graphen von (hier in grau abgebildet) ändert!
Beantworte anschließend die Fragen.
Für
Für
Für
Betrachte die abgebildeten Graphen und bestimme ihren Funktionsterm.
Wähle alle richtigen Aussagen aus.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?