Aufgaben zur Bestimmung von Wertebereichen
- 1
Bestimme den Wertebereich der Funktion bei maximalem Definitionsbereich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Bringe die quadratische Funktion auf die Scheitelform.
Lies den Scheitel und die Öffnungsrichtung ab.
, Parabel nach oben geöffnet
Gib die Wertemenge an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Bringe die quadratische Funktion auf die Scheitelform.
Lese Scheitel und Öffnungsrichtung ab.
, Parabel nach unten geöffnet
Gebe die Wertemenge an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Ganzrationale Funktionen dritten Grades haben keine Definitionslücken.
Außerdem gilt:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Betrachte die Sinusfunktion. Der Sinus nimmt bekanntlich nur Werte zwischen -1 und 1 an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Betrachte .
ist eine streng monoton steigende Exponentailfunktion, die nur Werte anninmmt, die größer als 0 sind.
Betrachte die Grenzwerte.
Gib nun den Wertebereich an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Bestimme den Definitionsbereich.
Bestimme die Grenzwerte.
Für den zweiten Grenzwert nutzt du aus, das der Logarithmus immer langsamer wächst als jedes Polynom.
Bestimme jetzt die Extrema.
Bestimme jetzt den y-Wert.
Da dies das einzige Extremum ist und die beiden Grenzwerte an den jeweiligen Definitionslücken rechts und links davon (also und) jeweils sind, ist das Extremum ein Minimum.
Gib jetzt den Wertebereich an.
Hast du eine Frage oder Feedback?
- 2
Ermittle den Wertebereich der zum Graphen zugehörigen Funktion f(x) mit .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich bestimmen
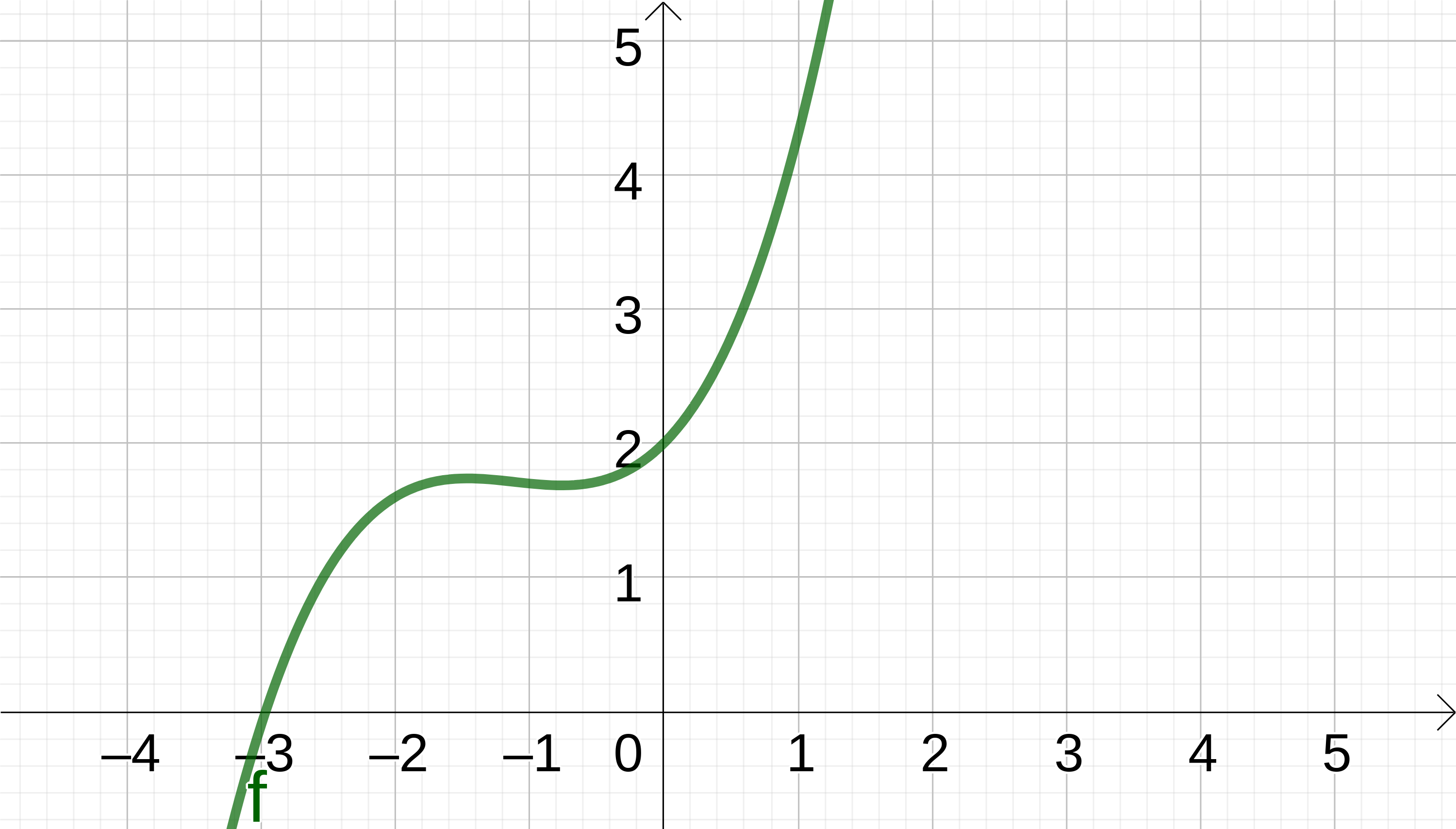
Zuerst einmal solltest du dir den Graphen anschauen. Um die Wertemenge herauszufinden musst du dir die/den höchsten bzw. niedrigsten klar definierbaren Punkt auf dem Graphen anschauen.
In diesem Fall geht der Graph in beide Richtungen ins Unendliche. Somit kannst du die angegebene Lösung ausschließen.
Jetzt musst du nur noch darauf achten, dass die Wertemenge richtig aufgeschrieben ist. Die eckigen Klammern müssen beim Unendlichkeitszeichen nach außen zeigen, da diese nicht begrenzt werden kann.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich bestimmen
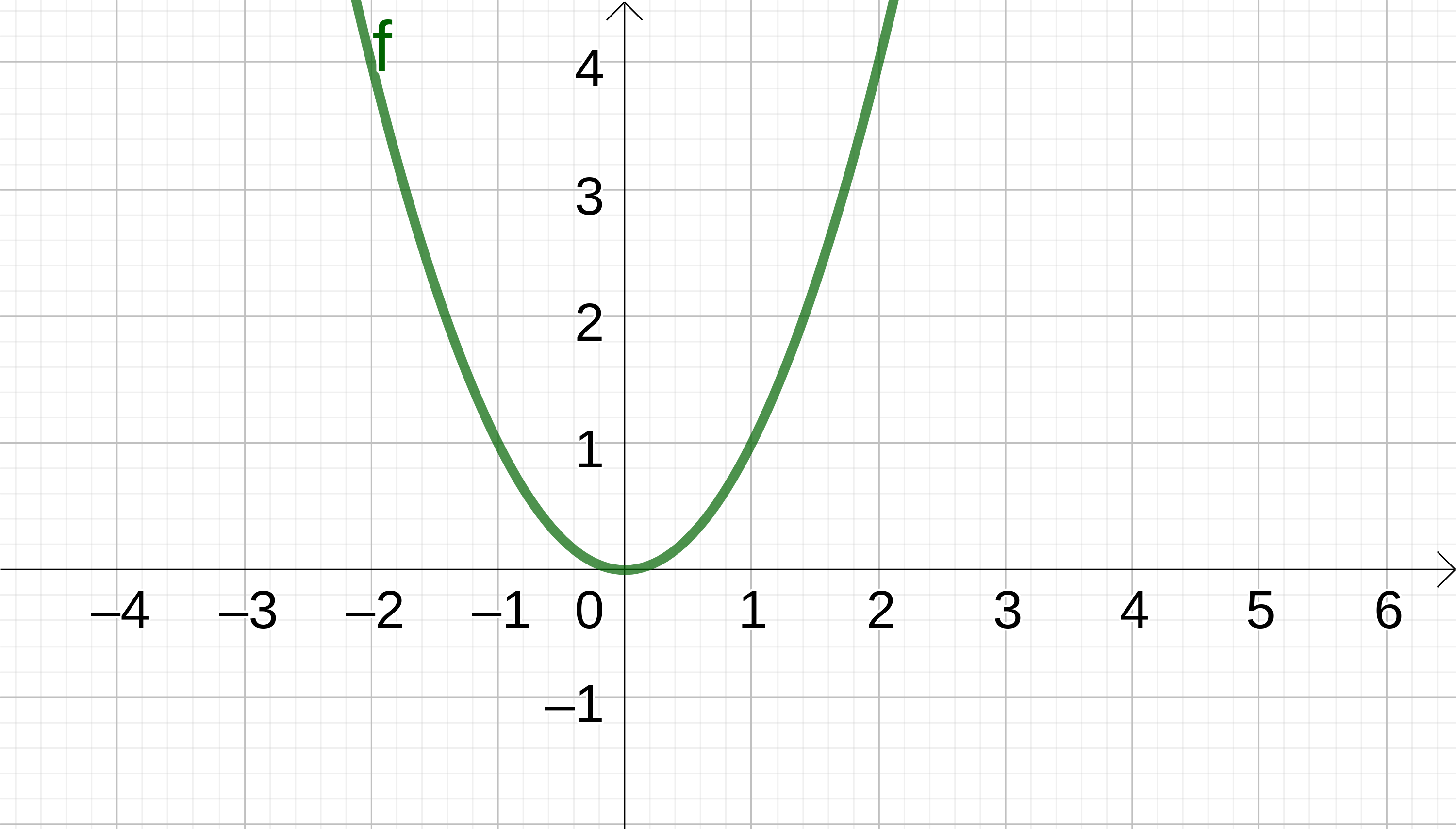
Betrachtest du den Graphen , wirst du bemerken, dass er einen tiefsten Punkt hat und deshalb nicht in die negative Unendlichkeit gehen kann. Der tiefste Punkt ist auf der y-Achste bei 0.
Nach oben hin lässt sich jedoch kein klar definierbarer höchster Punkt erkennen, folglich geht der Graph hier in die positive Unendlichkeit.
Wenn man nun diese Erkenntnisse kombiniert lässt sich sagen, dass die y-Werte von minimal 0 und maximal erreichen.
Daher gilt für die Wertemenge:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich bestimmen
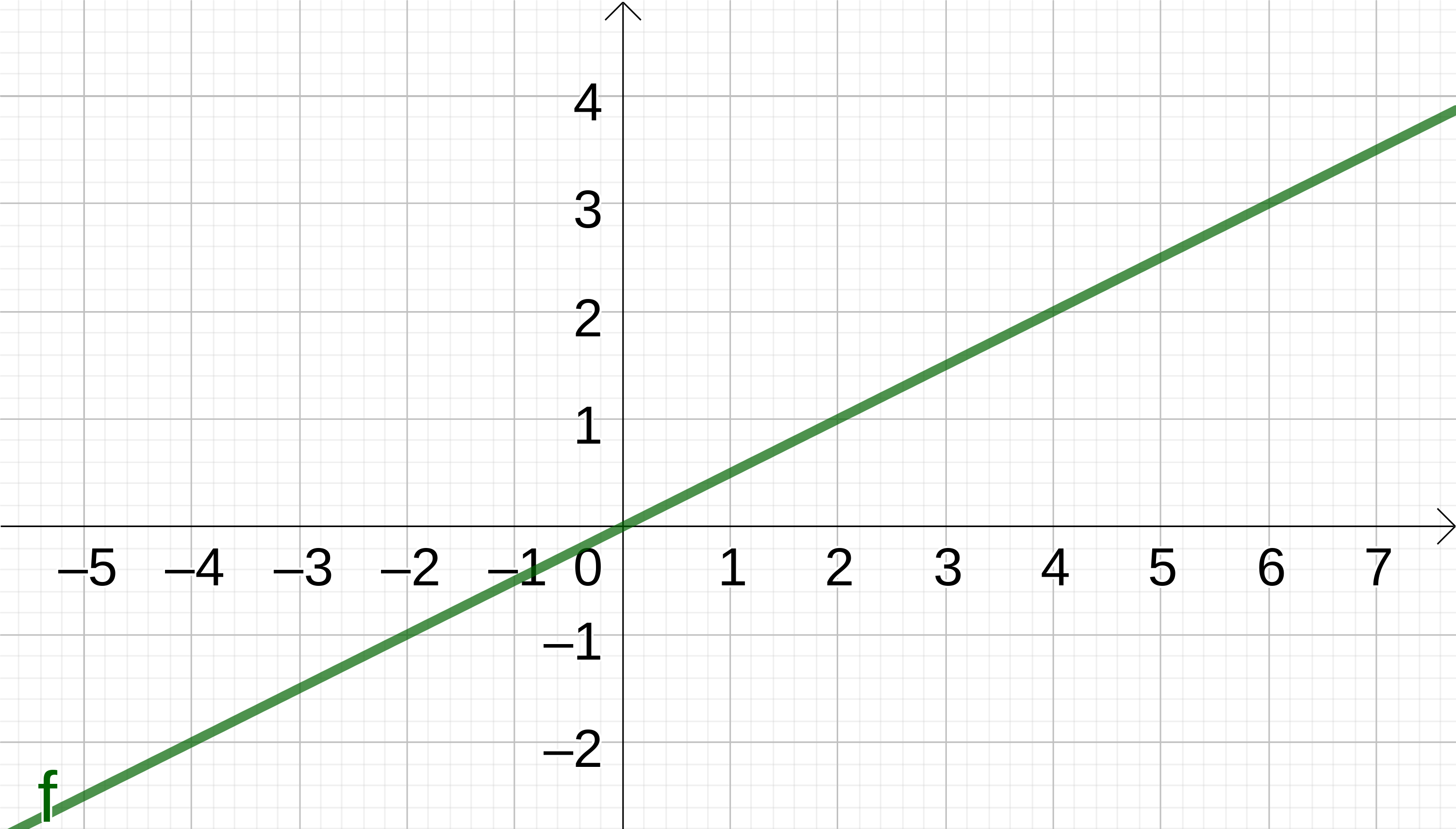
Da gilt, solltest du dir die y-Werte für alle x-Werte ansehen. Weil bspw. bei x=4, y=2 entspricht, lässt sich die Lösung schonmal nicht mit dem Graphen von verbinden.
Aber da der Graph nicht nur in die negative Unendlichkeit geht, sondern auch in die positive, gilt:
Hast du eine Frage oder Feedback?
- 3
Bestimme mithilfe des Graphen die Wertemenge von , für .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge einer Funktion
Da auf dem -Achsenabschnitt von bis die -Werte des Graphen minimal und maximal erreichen, gilt:
Betrachte das Verhalten des Graphen in dem Bereich, der auf der -Achse zwischen und liegt. Wie verhält sich dieser zu den möglichen -Werten?
- 4
Bestimme mit Hilfe des Graphen die Wertemenge von f(x) für .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge einer Funktion
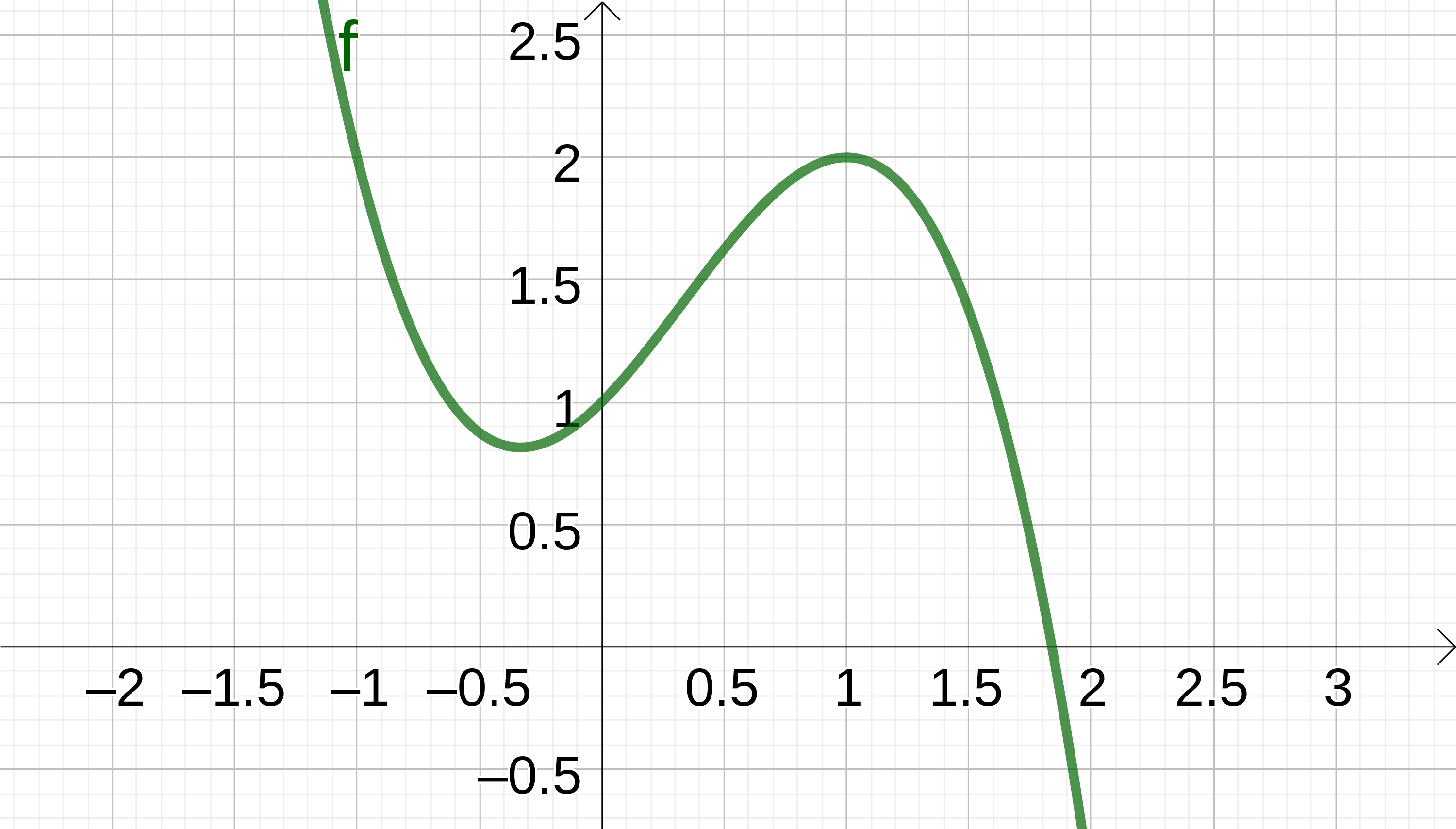
Den größten y-Wert, den die Funktion für positive x-Werte annimmt, ist . Nach unten ist sie nicht beschränkt. Deshalb ist der Wertebereich:
Betrachte das Verhalten des Graphen in dem Bereich, in dem alle x-Werte positiv sind. Beziehe dich auf die möglichen y-Werte.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

