Teil A

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Aufgaben
Welche beiden Aufgaben haben das gleiche Ergebnis? Klicke die beiden Aufgaben an.
15% von 400€
30% von 200€
20% von 400€
30% von 400€

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung

Lösung als Video

Lösung als Text

W: Prozentwert
G: Grundwert
p: Prozentsatz
Gesucht ist in unserer Aufgabe der Prozentwert.
W=p⋅GW=p\cdot G
1) 15% von 400€, W=0,15⋅400€=60€W=0,15\cdot400€=60€
2) 30% von 200€, W=0,30⋅200€=60€W=0,30\cdot200€=60€
2) 20% von 400€, W=0,20⋅400€=80€W=0,20\cdot400€=80€
4) 30% von 400€, W=0,30⋅400€=120€W=0,30\cdot400€=120€
Die Aufgaben 11 und 22 haben das gleiche Ergebnis.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Ergänze die fehlenden Angaben zu den Temperaturänderungen:
Temperaturaufgabe

Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen

Lösung als Video

Lösung als Text

Bezeichnung:
Mit xx wir die gesuchte Temperaturangabe im linken Kästchen bezeichnet.
x+9∘=−18∘∣−9∘x+9^\circ=-18^\circ \qquad\qquad\qquad\quad | -9^\circ
x+9°−9°=−18∘−9∘x+9°-9°=-18^\circ-9^\circ \qquad \quad fasse zusammen
x=−27∘x=-27^\circ
Bezeichnung:
Mit yy wir die gesuchte Temperaturangabe im rechten Kästchen bezeichnet.
−18∘+y=12∘∣+18∘-18^\circ+y=12^\circ \qquad\qquad\qquad |+18^\circ
−18°+y+18°=12∘+18∘-18°+y+18°=12^\circ+18^\circ \qquad \quad fasse zusammen
y=30∘y=30^\circ
−27∘+9∘=18∘−18∘+30∘=12∘\begin{array}{l}-27^\circ+9^\circ=18^\circ\\-18^\circ+30^\circ=12^\circ\end{array}
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Richtig oder falsch?
Kommentieren
1,1⋅1,1=1,111,1\cdot1,1=1,11
richtig
falsch

Multiplikation von Dezimalbrüchen

Für diese Aufgabe musst du die Multiplikation von Dezimalbrüchen beherrschen.
%%\begin{array}{l}\,\,\, \,\,1,1\cdot1,1 = 1,21 \\\,\,\,\,\,\,\underline{+1,1}\\ \,\,\,\,\,\,1,21\ \\ \end{array}%%
Die Lösung 1,1⋅1,1=1,111,1\cdot1,1=1,11 ist falsch.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
71\begin{array}{l}\sqrt{71}\\\end{array} liegt zwischen 8 und 9
richtig
falsch

Potenzen und Wurzeln

Für diese Aufgabe musst du Potenzen und Wurzeln berechnen können.
82=6492=8164<71<81\begin{array}{l}8^2=64\\9^2=81\\64<71<81\end{array}
64<71<81\sqrt{64}<\sqrt{71}<\sqrt{81}
8<71<98<\sqrt{71}<9
Die Aussage 71\sqrt{71} liegt zwischen 88 und 99 ist richtig.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
0,825+0,085=0,910,825+0,085=0,91
richtig
falsch

Addition von Kommazahlen

Für diese Aufgabe musst du die Addition von Kommazahlne beherrschen.
%%\begin{array}{l}\,\,\, \,\,\,\,\,\,\,\,0,825+0,085= 0,91 \\\,\,\,\,\,\,\underline{+0,085}\\ \,\,\,\,\,\,\,\,\,\,\,0,910\ \\ \end{array}%%
Die Lösung 0,825+0,085=0,91  0,825+0,085=0,91\; ist richtig.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
8⋅x−6=72x=12\begin{array}{l}8\cdot x-6=72\\x=12\end{array}
richtig
falsch

Umformung von Gleichungen

Für diese Aufgabe musst du die Umformung von Gleichungen beherrschen.
8⋅x−6=728\cdot x-6=72
| +6+6
8⋅x−6+6=72+68\cdot x-6+6=72+6
fasse zusammen
8x=788x=78
| :8:8
x=788=9,75x=\frac{78}8=9,75
Die Aussage x=12x=12 ist falsch.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
In dem Dreieck gilt α=βα=β. Berechne die Größe des Winkels γ.
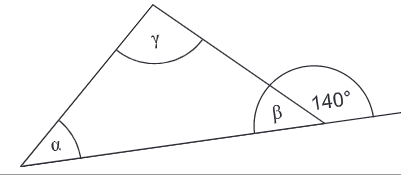
Dreieck
Hinweis: Skizze nicht maßstabsgetreu.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nebenwinkel

Lösung als Video

Lösung als Text

Für diese Aufgabe musst du die Eigenschaften von Nebenwinkeln und die Summe der Innenwinkel im Dreieck kennen.
Die Summe der Nebenwinkel beträgt 180∘180^\circ.
β+140°\beta+140°==180°180°|−140°-140°
β+140°−140°\beta+140°-140°==180°−140°180°-140°
↓
Fasse zusammen
β\beta==40°40°|α=β\alpha=\beta
==40°40°
Die Summe der Innenwinkel im Dreieck beträgt 180∘180^\circ.
α+β+γ\alpha+\beta+\gamma==180°180°
↓
Setze für α\alpha und β\beta die Werte ein.
40°+40°+γ40°+40°+\gamma==180°180°
↓
Fasse zusammen
80°+γ80°+\gamma==180°180°|−80°-80°
γ\gamma==100°100°
Die Größe des Winkels γ\gamma beträgt 100∘100^\circ.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
In einem Supermarkt werden Chips in verschiedenen Packungsgrößen angeboten. Paul will für seine Party 1 kg Chips kaufen.
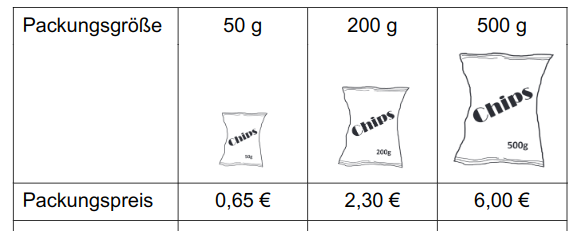
Preistabelle
Bestimme jeweils den Preis für 1 kg und wähle dann das günstigste Angebot aus.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Gewichten

Lösung als Video

Lösung als Text



1kg=1000g1kg=1000g
1) Packungsgröße 50g50g, Packungspreis 0,65€0,65€.
Berechne zunächst die Anzahl der Packungen, wenn du 1kg1kg Chips kaufen möchtest.
1000g:50g=201000g:50g=20
Von den 50g50g Packungen benötigt du 20 Stück.
Berechne nun den Preis für diese 2020 Packungen.
20⋅0,65€=13€20\cdot0{,}65€=13€
Bei einer Packungsgröße von 50g50g kostet 1kg1kg Chips 13€13€.
2) Packungsgröße 200g200g, Packungspreis 2,30€2,30€.
Berechne zunächst die Anzahl der Packungen, wenn du 1kg1kg Chips kaufen möchtest.
1000g:200g=51000g:200g=5
Von den 200g200g Packungen benötigt du 5 Stück.
Berechne nun den Preis für diese 55 Packungen.
5⋅2,30€=11,50€5\cdot2{,}30€=11{,}50€
Bei einer Packungsgröße von 200g200g kostet 1kg1kg Chips 11,50€11{,}50€
3) Packungsgröße 500g500g, Packungspreis 6,00€6{,}00€.
Berechne zunächst die Anzahl der Packungen, wenn du 1kg1kg Chips kaufen möchtest.
1000g:500g=21000g:500g=2
Von den 500g500g Packungen benötigt du 2 Stück.
Berechne nun den Preis für diese 22 Packungen.
2⋅6,00€=12,00€2\cdot6{,}00€=12{,}00€
Bei einer Packungsgröße von 500g500g kostet 1kg1kg Chips 12,00€12{,}00€.
55 Tüten mit jeweils 200g200g sind das günstigste Angebot.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
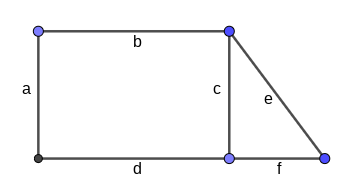
Der Flächeninhalt des Rechtecks beträgt 96cm296cm^2. Berechne den Umfang der gesamten Figur.
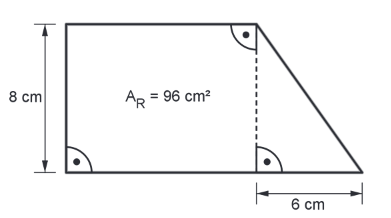Erweitertes Rechteck

Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche eines Rechtecks

Videolösung

Für diese Aufgabe musst du wissen, wie man die Fläche eines Rechtecks berechnet und den Satz des Pythagoras kennen.
Skizze zu Erweitertes Rechteck
Berechne zunächst die Seitenlänge bb des Rechtecks. Dies kannst du tun, da die Fläche des Rechtecks und eine Seitenlänge des Rechtecks bekannt sind.
Die Fläche eines Rechtecks ist das Produkt zweier beliebig aneinander liegender Seiten:
A=a⋅bA=a\cdot b
96cm296cm^2==8cm⋅b8cm\cdot b|:8:8
96 cm2:8=b96\,cm^2:8=b
b=12 cmb=12\,cm
Die zweite Seitenlänge bb des Rechtecks beträgt 12 cm12\,cm.
Gegenüberliegende Seiten eines Rechtecks sind gleich lang.
⇒a=c          b=d\begin{array}{l}\Rightarrow a=c\\\;\;\;\;\;b=d\end{array}
Für die Berechnung der Grundlinie ee des rechten Dreiecks benötigst du den Satz des Pythagoras.
e2e^2==c2+f2c^2+f^2
↓
Setze die Werte ein.
e2e^2==(8cm)2+(6cm)2\left(8cm\right)^2+\left(6cm\right)^2
↓
Rechne die Klammern aus.
e2e^2==64cm2+36cm264cm^2+36cm^2
↓
Fasse zusammen.
e2e^2==100cm2100cm^2
↓
Ziehe die Wurzel.
ee==10cm10cm
Die Länge der Grundlinie ee des Dreicks beträgt e=10cme=10cm.
Der Umfang der gesamten Figur ergibt sich aus:
UU==a+b+e+f+da+b+e+f+d
↓
Setze die Werte ein.
UU==8cm+12cm+10cm+6cm+12cm8cm+12cm+10cm+6cm+12cm
↓
Fasse zusammen
UU==48cm48cm
Der Umfang der gesamten Figur beträgt 48 cm48 \, cm.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
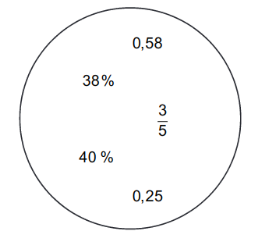
Setze jeweils eine der gegebenen Zahlen aus dem Kreis ein, sodass korrekte Aussagen entstehen.
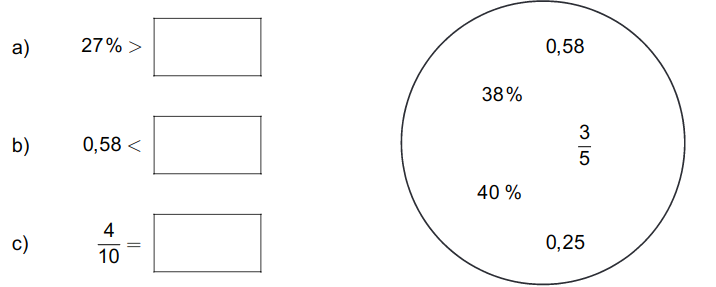
Prozent

Videolösung

Textlösung

Prozent, Hundertstel-Bruch, Dezimalbruch

Für diese Aufgabe musst du den Zusammenhang zwischen Prozent, Hundertstel-Bruch und Dezimalbruch kennen.
Rechne die Werte im Kreis um.
Kreis

Teilaufgabe a)

0,25=25100=25%0,25=\frac{25}{100}=25\% 
=> 27%>0,2527\%>0,25

Teilaufgabe b)

35=610=0,60\frac{3}{5}=\frac{6}{10}=0,60
=> 0,58<350,58<\frac35

Teilaufgabe c)

40%=40100=41040\%=\frac{40}{100}=\frac{4}{10}
=> 410=40%\frac{4}{10}=40\% 
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
In jedes Gefäß werden 500 cm³ Wasser eingefüllt.
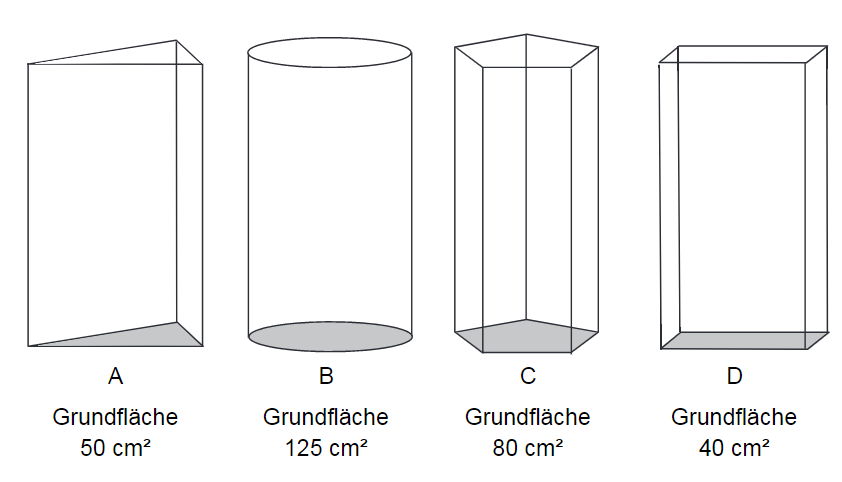
Gefäße
Ergänze die beiden Sätze zu einer wahren Aussage.
Im Gefäß ____ steht das Wasser am höchsten.
Im Gefäß ____ steht das Wasser am niedrigsten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen eines Körpers

Videolösung

Textlösung

V=G⋅h⇒h=V:GV=G\cdot h \Rightarrow h=V:G
Gefäß A: h=500 cm350 cm2=10 cmh=\dfrac{500\ \text{cm}^3}{50\ \text{cm}^2}=10\ \text{cm}
Gefäß B: h=500 cm3125 cm2=4 cmh=\dfrac{500\ \text{cm}^3}{125\ \text{cm}^2}=4\ \text{cm}
Gefäß C: h=500 cm380 cm2=6,25 cmh=\dfrac{500\ \text{cm}^3}{80\ \text{cm}^2}=6{,}25\ \text{cm}
Gefäß D: h=500 cm340 cm2=12,5 cmh=\dfrac{500\ \text{cm}^3}{40\ \text{cm}^2}=12{,}5\ \text{cm}
Im Gefäß D steht das Wasser am höchsten. Im Gefäß B steht das Wasser am niedrigsten.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
In einem Freibad gibt es unterschiedliche Preise für Kinder und Erwachsene. Drei Kinder bezahlen zusammen 10,20 €. Für zwei Erwachsene und ein Kind kostet der Eintritt insgesamt 18,40 €. Ergänze die Preisliste.
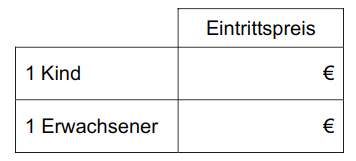
Preisliste

Videolösung

Textlösung

33 Kinder zahlen zusammen 10,20€10,20€.
Ein Kind bezahlt
10,20€:3=3,40€.\displaystyle 10,20€:3=3,40€.
Pro Kind beträgt der Eintritt also 3,40€3,40€.
22 Erwachsene und 11 Kind bezahlen gemeinsam 18,40€18,40€.
22 Erwachsene bezahlen also
18,40€−3,40€=15,00€.\displaystyle 18,40€-3,40€=15,00€.
Jeder Erwachsene bezahlt
15,00€:2=7,50€.\displaystyle 15,00€:2=7,50€.
Pro Erwachsener beträgt der Eintritt also 7,50€7,50€.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Ein Regal mit zwei gleich hohen Fächern soll mit Schachteln befüllt werden (siehe Skizze). Wie viele Schachteln mit den angegebenen Maßen passen maximal in das Regal?
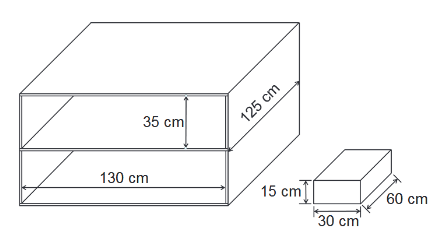Regal mit Schachteln

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Einheiten

Textlösung

Die Fachhöhe beträgt 35 cm35\ \text{cm}. Da die Höhe der Schachteln 15 cm15\ \text{cm} beträgt, passen jeweils 35:15=2,33…35:15=2,33\ldots, also 22 Schachteln pro Fach übereinander.

Die Fachbreite beträgt 130 cm130\ \text{cm}. Da die Breite der Schachteln 30 cm30\ \text{cm} beträgt, passen 130:30=4,33…130:30=4,33…, also 44 Schachteln pro Fach nebeneinander.

Die Fachlänge beträgt 125 cm125\ \text{cm}. Da die Länge der Schachteln 60 cm60\ \text{cm} beträgt, passen 125:60=2,083125:60=2,083, also 22 Schachteln pro Fach hintereinander.
In jedes der beiden Fächer passen also 2⋅4⋅2=16  2\cdot4\cdot2=16\;Schachteln.
In beiden Fächern haben insgesamt 2⋅16=32  2\cdot16=32\;Schachteln Platz.

Videolösung

Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
An der Ostsee steht der größte Strandkorb der Welt, auf dem mehrere Personen nebeneinander sitzen können (siehe Foto). Schätze die Breite des Strandkorbs ab. Beschreibe dein Vorgehen und begründe rechnerisch.
Strandkorb

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schätzen

Videolösung

Textlösung

Um die Breite des Strandkorbs zu bestimmen, brauchst du ein Vergleichsobjekt, dessen Größe du in etwa kennst.

Im Bild sieht man drei Personen auf dem Strandkorb sitzen. Daher bietet es sich an, zu schätzen, wie breit diese Personen in etwa sind.

Die Personen haben circa eine Breite von je 30cm30\text{cm}. Sie sitzen jeweils auf einem der farbigen Streifen mit ein wenig Abstand. Also sind die farbigen Streifen in etwa 40cm40\text{cm}_{ } breit.

Wenn einer der Streifen 40cm40\text{cm} hat, kann man die Breite des Strandkorbs anhand der Anzahl der Streifen abschätzen. Im Bild sieht man 6 weiße und 7 schwarze Streifen. Also ist die Sitzfläche ungefähr 40cm⋅(6+7)=40cm⋅13 = 520 cm 40\text{cm}\cdot\left(6+7\right)=40\text{cm}\cdot13\ =\ 520\ \text{cm}\ breit.

Die Seitenverkleidung nimmt in etwa noch eine Streifenbreite ein. Also ist der Strandkorb 520cm + 40cm = 560cm = 5,6 m 520\text{cm}\ +\ 40\text{cm}\ =\ 560\text{cm}\ =\ 5,6\ \text{m}\ breit.

Hinweis: Zu dieser Aufgabe gibt es viele verschiedene Herangehensweisen. Es ist vor allem wichtig, schlüßig zu erklären, welche Annahmen und Vergleichsmaßstäbe du benutzt. Zum Beispiel kannst du eine andere Breite der Menschen wählen.
Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. Information
Kommentieren Kommentare
0
Zu curriculum-topic-folder Teil A:
Emanuel 2019-07-03 15:28:16+0200
750 cm durchschnitt des Menschenkörpers in der breite 40-50 cm mal den Streifenmuster abschnitt 15
kathongi 2019-07-04 08:44:43+0200
Hey Emanuel,
wenn das deine Lösung zu Aufgabe 11 sein soll, wäre min. ein Satz hilfreich, um deine Denkweise besser verstehen zu können ;)
Soll 750cm die Breite des Strandkorbs sein? Falls du auf eine sinnvolle Lösung kommst, kannst du diese fehlende Lösung gerne selbst hinzufügen über den Stift neben der Aufgabe :)
Gruß, Kathongi