1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, wie du Brüche ordnest und vergleichst.

Erforderliches Vorwissen:
Dauer
Die Bearbeitung des Kurses dauert ca. 45 min.
2 Kuchen backen
Brüche können dir immer wieder im Alltag begegnen.
Zum Beispiel beim Backen. In der Rezeptur stehen häufig Literangaben wie , oder .
Hier wäre es hilfreich erkennen zu können, welcher Bruch der Größere ist, um besser abzuschätzen, wie viel du von welcher Zutat brauchst.

3 Gleicher Nenner unterschiedlicher Zähler
Haben Brüche den gleichen Nenner, aber einen unterschiedlichen Zähler, dann sind sie gleichnamig. Das heißt, um den Bruch nach der Größe zu ordnen, betrachtest du nur den Zähler. Der Bruch mit dem kleineren Zähler ist gleichzeitig der kleinere Bruch.
Gleicher Nenner und unterschiedlicher Zähler, dann ist der Bruch mit dem kleineren Zähler der kleinere Bruch.
Beispiel:
Zwei gleichnamige Brüche werden verglichen:
;
Die Brüche haben den gleichen Nenner 8, aber unterschiedliche Zähler. Der erste Bruch ist der kleinere Bruch, da der Zähler kleiner ist, als bei .
Daraus folgt:
Der Bruch ist kleiner als .
Grafisch dargestellt:
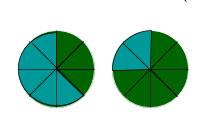
Beide Pizzen wurden in acht Stücke geschnitten. Bei beiden Pizzen sind noch Stücke da (grün gefärbt). Bei der ersten Pizza sind noch drei Stücke übrig (im Bruch ). Bei der zweiten Pizza sogar noch sechs (im Bruch ). Also sind bei der zweiten Pizza noch mehr Stücke übrig.
Daraus ergibt sich .
4 Aufgaben zu Gleicher Nenner unterschiedlicher Zähler
Laden
5 Gleicher Zähler unterschiedlicher Nenner
Auf der vorherigen Seite ,,Gleicher Nenner, unterschiedlicher Zähler" hast du gelernt, dass man beim Ordnen von Brüchen mit gleichem Nenner und unterschiedlichem Zähler nur den Zähler betrachtet. Um Brüche mit gleichem Zähler, aber unterschiedlichem Nenner der Größe nach zu ordnen, betrachtest du nur den Nenner. Der Bruch mit dem kleineren Nenner ist der größere Bruch.
Gleicher Zähler und unterschiedlichen Nenner, dann ist der Bruch mit dem größeren Nenner, der kleinere Bruch.
Beispiel:
Zwei Brüche mit gleichem Zähler werden verglichen.
Daraus folgt:
Der Bruch ist größer als .
Grafisch dargestellt:
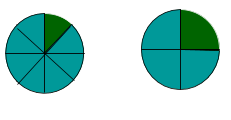
Bei beiden Pizzen ist jeweils noch ein Stück übrig. Die erste Pizza wurde in 8 Stücke geschnitten (im Bruch ). Die zweite Pizza wurde in vier Stücke geschnitten (im Bruch ). Du kannst sehen, dass bei der zweiten Pizza das übrige Stück (grün gefärbt) doppelt so groß ist, wie das übrige Stück der ersten Pizza. Daraus ergibt sich .
6 Aufgaben zu gleicher Zähler unterschiedlicher Nenner
Ordne die folgenden Brüche von klein nach groß.
Laden
7 Unterschiedlicher Zähler und Nenner
Unterschiedliche Nenner und unterschiedliche Zähler, dann durch Kürzen oder Erweitern auf den Hauptnenner bringen.
1. Beispiel:
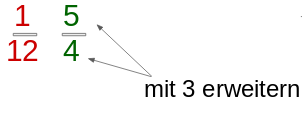
Zwei ungleichnamige Brüche werden durch Erweitern verglichen.
Durch Erweitern der Brüche auf den gleichen Nenner, kannst du leichter erkennen, welcher der größere Bruch ist.
Erweitert ergeben die Brüche: und
Daraus folgt:
Der Bruch ist der kleinere Bruch, da hier der Zähler kleiner ist, als bei .
2. Beispiel:
Zwei ungleichnamige Brüche werden durch Kürzen verglichen.
Durch Kürzen der Brüche auf den Hauptnenner, kannst du leichter erkennen, welcher der größere Bruch ist.
Gekürzt mit 2 ergeben die Brüche: und .
Daraus folgt:
Der Bruch ist kleiner als .
Grafisch dargestellt:
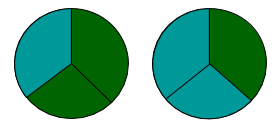
Beide Pizzen wurden jeweils in drei Stücke geschnitten. Bei der ersten sind noch zwei übrig (im Bruch ). Bei der zweiten ist nur noch ein Stück übrig (im Bruch ). Du kannst sehen, dass bei der ersten Pizza noch mehr zum Essen da ist. Daraus ergibt sich .
8 Aufgaben zu unterschiedlichen Zähler und Nenner
9 Gemischte Aufgaben
Laden
10 Zusammenfassung
In diesem Kurs hast du gelernt, wie du zwei oder mehr Brüche nach der Größe ordnest. Nun kannst du Brüche mit gleichem Nenner und unterschiedlichem Zähler ordnen.
Gleicher Nenner und unterschiedlicher Zähler, dann ist der Bruch mit dem kleineren Zähler der kleinere Bruch.
Genauso kannst du nun Brüche mit gleichem Zähler und unterschiedlichem Nenner ordnen.
Gleicher Zähler und unterschiedlichen Nenner, dann ist der Bruch mit dem größeren Nenner, der kleinere Bruch.

Ebenfalls kannst du auch Brüche mit unterschiedlichem Nenner und Zähler nach der Größe ordnen und vergleichen.
Unterschiedliche Nenner und unterschiedliche Zähler, dann durchs Kürzen oder Erweitern auf den Hauptnenner bringen.