Aufgaben zu Kugeln, Ebenen und Tangentialebenen

Gegeben ist die Kugel K mit der Gleichung $K : [\vec{x} - (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array})] \circ [\vec{x} - (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array})] = 36$ und die Ebene $E_{1} : 4 x_{1} + 4 x_{2} + 2 x_{3} = - 22$ .

1) Zeige, dass $E_{1}$ Tangentialebene an $K$ ist und berechne den Berührpunkt $B$ .

2) Durch $F_{a} : 2 \cdot x_{1} + 4 \cdot x_{2} + 6 \cdot x_{3} = a$ wird eine Ebenenschar bestimmt. Berechne für welche Parameterwerte die Kugel $K$ und die Ebene $F_{a}$

gemeinsame Punkte haben. Bestimme für welche Werte von $a$ ein Schnittkreis mit Radius $r = 2,2$ entsteht und berechne die zugehörigen Kreismittelpunkte.

3) Der Punkt $A (8 | 2 | - 1)$ liegt auf $K$ . Stelle die Gleichung der Tangentialebene $E_{2}$ in $A$ in Koordinatenform auf.

4) Die Ebenen $E_{1}$ und $E_{2}$ bilden eine Rinne für die Kugel $K$ , in der diese entlang rollt. Gib eine Gleichung der Geraden $g$ an, auf der sich der Mittelpunkt $M$ der Kugel bewegt.

5) Die Ebene $E_{3} : 2 x_{2} - 4 x_{3} = - 96$ steht senkrecht zu $E_{1}$ und $E_{2}$ . Berechne die Länge der Strecke die die Kugel $K$ vom Startpunkt aus zurücklegt, bis diese von $E_{3}$ gestoppt wird.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis und Kugel

Teilaufgabe 1

Bestimmung der Art des Schnitts von Ebene und Kugel

Um die hessesche Normalenform einer Ebene zu berechnen, teilt man die Ebenengleichung in Koordinatenform durch den Betrag des Normalenvektors $| \vec{n} |$ . Wenn die Koordinatengleichung der Ebene gegeben ist, kann der Normalenvektor aus der Koordinatengleichung der Ebene abgelesen werden. Die Koeffizienten in der Ebenengleichung ergeben den Normalenvektor.

\vec{n} = (\begin{array}{c} 4 \\ 4 \\ 2 \end{array}) \Rightarrow | \vec{n} | = \sqrt{4^{2} + 4^{2} + 2^{2}} = \sqrt{36} = 6

H N F : \frac{4 x_{1} + 4 x_{2} + 2 x_{3} + 22}{6} = 0

Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein:

\begin{array}{rcl} d (M, E) & = & | \frac{4 \cdot 2 + 4 \cdot 2 + 2 \cdot (- 1) + 22}{6} | \\ = & | \frac{36}{6} | \\ = & 6 \end{array}

Der Abstand des Kugelmittelpunktes von der Ebene $E_{1}$ beträgt $6$ und ist somit gleich dem Kugelradius $r = 6.$

Antwort: Die Ebene $E_{1}$ ist eine Tangentialebene.

Berechnung des Berührpunktes $B$

Stelle die Gleichung der Lotgeraden von $M$ auf die Ebene $E_{1}$ auf, indem Du für den Stützvektor den Vektor zum Kugelmittelpunkt und als Richtungsvektor den Normalenvektor $\vec{n}$ der Ebene $E_{1}$ verwendest.

g_{L o t} : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + t \cdot (\begin{array}{c} 4 \\ 4 \\ 2 \end{array})

Schneide $g_{L o t}$ mit der Ebene $E_{1}$ :

\begin{array}{rcl} 4 \cdot (2 + 4 t) + 4 \cdot (2 + 4 t) + 2 \cdot (- 1 + 2 t) + 22 & = & 0 \\ 8 + 16 t + 8 + 16 t - 2 + 4 t + 22 & = & 0 \\ 36 t & = & - 36 \\ t & = & - 1 \end{array}

Setze $t = - 1$ in die Geradengleichung ein und Du erhältst den Vektor zum Berührpunkt $B$ .

$\begin{array}{l} \vec{x_{B}} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + (- 1) \cdot (\begin{array}{c} 4 \\ 4 \\ 2 \end{array}) = (\begin{array}{c} - 2 \\ - 2 \\ - 3 \end{array}) \\ \Rightarrow B (- 2 | - 2 | - 3) \end{array}$

Antwort: Der Berührpunkt $B$ zwischen der Kugel und der Ebene $E_{1}$ hat folgende Koordinaten:

B (- 2 | - 2 | - 3)

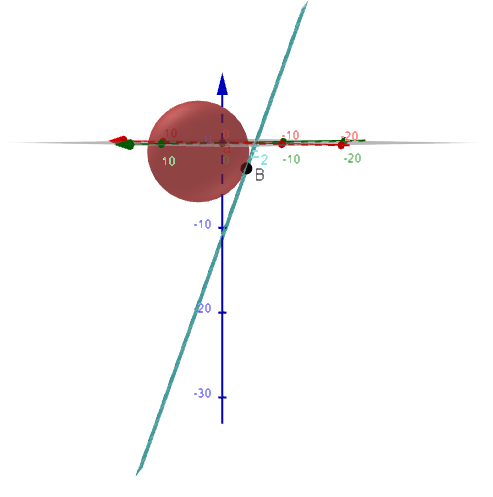
Die nebenstehende Abb. ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.

Dargestellt sind die Kugel $K$ , die Ebene $E_{1}$ und der Berührpunkt $B$ .

Teilaufgabe 2

Bestimmung der hessischen Normalenform der Ebenenschar $F_{a}$

Berechne zunächst den Normalenvektor der Ebenenschar:

\vec{n} = (\begin{array}{c} 2 \\ 4 \\ 6 \end{array}) \Rightarrow | \vec{n} | = \sqrt{2^{2} + 4^{2} + 6^{2}} = \sqrt{56}

Die Ebenengleichung $F_{a}$ in Koordinatenform wird durch den Betrag des Normalenvektors $| \vec{n} |$ geteilt und Du erhältst die hessesche Normalenform.

H N F : \frac{2 x_{1} + 4 x_{2} + 6 x_{3} - a}{\sqrt{56}} = 0

Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein und verlange, dass der berechnete Abstand kleiner als der Kugelradius ist :

\begin{aligned} d (M, F_{a}) = | \frac{2 \cdot 2 + 4 \cdot 2 + 6 \cdot (- 1) - a}{\sqrt{56}} | < & 6 \\ | \frac{6 - a}{\sqrt{56}} | < & 6 | \cdot \sqrt{56} \\ | 6 - a | < & 6 \cdot \sqrt{56} \end{aligned}

Führe nun eine Fallunterscheidung durch:

\begin{array}{cccccccl} 6 - a > & 0 & | & I \\ 6 - a < & 0 & | & II \end{array}

Aus $I$ folgt:

6 - a < 6 \cdot \sqrt{56} \Rightarrow a > 6 - 6 \cdot \sqrt{56} \approx - 38,9

Aus $II$ folgt:

- (6 - a) < 6 \cdot \sqrt{56} \Rightarrow - 6 + a < 6 \cdot \sqrt{56} \Rightarrow a < 6 + 6 \cdot \sqrt{56} \approx 50,9

Antwort: Wenn der Parameter $a$ größer als $6 - 6 \cdot \sqrt{56}$ oder kleiner als $6 + 6 \cdot \sqrt{56}$ ist, haben die Ebene $F_{a}$ und die Kugel $K$ gemeinsame Punkte, d.h. es gibt einen Schnittkreis.

Bestimmung des Parameter $a$ , so dass der Schnittkreisradius $r = 2,2$ beträgt

Den Abstand $d$ des Mittelpunktes $M^{'}$ vom Mittelpunkt $M$ berechnest Du mit Hilfe des Satzes von Pythagoras.

$\begin{array}{rcl} d & = & \sqrt{r^{2} - {r^{'}}^{2}} \\ = & \sqrt{6^{2} - {2,2}^{2}} \\ = & \sqrt{31,16} \\ \approx & 5,58 \end{array}$

Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein.

(Diesen Rechenschritt hast Du schon zu Beginn der Teilaufgabe 2 gelöst.)

Verlange, dass der berechnete Abstand gleich $\sqrt{31,16}$ ist. Du erhältst folgende Gleichung:

\begin{aligned} \sqrt{31,16} & = | \frac{6 - a}{\sqrt{56}} | | \cdot \sqrt{56} \\ \sqrt{31,16} \cdot \sqrt{56} & = | 6 - a | \\ \sqrt{1744,96} & = | 6 - a | \end{aligned}

Führe nun eine Fallunterscheidung durch:

\begin{array}{cccccccl} 6 - a > & 0 & | & I \\ 6 - a < & 0 & | & II \end{array}

Aus $I$ folgt:

6 - a = \sqrt{1744,96} \Rightarrow a = 6 - \sqrt{1744,96} \approx - 35,77

Aus $II$ folgt:

- (6 - a) = \sqrt{1744,96} \Rightarrow - 6 + a = \sqrt{1744,96} \Rightarrow

a = 6 + \sqrt{1744,96} \approx 47,77

Antwort: Du hast zwei Parameter erhalten. Für $a = 6 - \sqrt{1744,96}$ bzw. $a = 6 + \sqrt{1744,96}$ haben die Ebenen $F_{a}$ einen Schnittkreisradius von $r = 2,2$ .

Bestimmung des Mittelpunktes $M^{'}$ des Schnittkreises

Du berechnest die Lotgerade von $M$ auf die Ebene $F_{a}$ . Dazu verwendest Du den Vektor zum Kugelmittelpunkt als Stützvektor und als Richtungsvektor nimmst Du den Normalenvektor $\vec{n}$ der Ebene $F_{a}$ .

g_{L o t} : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 4 \\ 6 \end{array})

Schneide $g_{L o t}$ mit der Ebene $F_{a}$ :

\begin{array}{rcl} 2 \cdot (2 + 2 t) + 4 \cdot (2 + 4 t) + 6 \cdot (- 1 + 6 t) - a & = & 0 \\ 4 + 4 t + 8 + 16 t - 6 + 36 t - a & = & 0 \\ 56 t + 6 - a & = & 0 \\ t & = & \frac{a - 6}{56} \end{array}

Für $a$ gibt es zwei Werte, so dass sich zwei Parameterwerte für $t$ ergeben:

\begin{array}{l} t_{1} = \frac{6 - \sqrt{1744,96} - 6}{56} = - \frac{\sqrt{1744,96}}{56} \approx - 0,746 \\ t_{2} = \frac{6 + \sqrt{1744,96} - 6}{56} = \frac{\sqrt{1744,96}}{56} \approx 0,746 \end{array}

Setze $t_{1}$ in die Geradengleichung ein und Du erhältst den Vektor zum Schnittkreismittelpunkt $M_{1}^{'}$ :

$\begin{array}{l} \vec{x_{M_{1}^{'}}} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) - \frac{\sqrt{1744,96}}{56} \cdot (\begin{array}{c} 2 \\ 4 \\ 6 \end{array}) \approx (\begin{array}{c} 0,5081 \\ - 0,9838 \\ - 5,4756 \end{array}) \\ \Rightarrow M_{1}^{'} (0,5081 | - 0,9838 | - 5,4756) \end{array}$

Setze $t_{2}$ in die Geradengleichung ein und Du erhältst den Vektor zum Schnittkreismittelpunkt $M_{2}^{'}$ :

$\begin{array}{l} \vec{x_{M_{2}^{'}}} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + \frac{\sqrt{1744,96}}{56} \cdot (\begin{array}{c} 2 \\ 4 \\ 6 \end{array}) \approx (\begin{array}{c} 3,4919 \\ 4,9838 \\ 3,4756 \end{array}) \\ \Rightarrow M_{2}^{'} (3,4919 | 4,9838 | 3,4756) \end{array}$

Antwort: Für die Schnittkreismittelpunkte ergeben sich die gerundeten Koordinaten $M_{1}^{'} (0,5081 | - 0,9838 | - 5,4756)$ und $M_{2}^{'} (3,4919 | 4,9838 | 3,4756)$ .

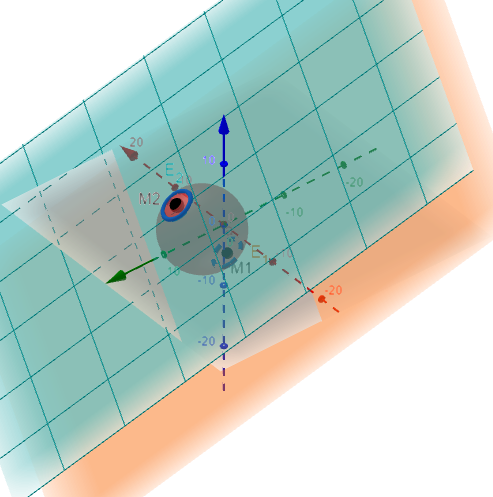
Die nebenstehende Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.

Dargestellt sind die Kugel $K$ , die Ebenen $F_{47,77}$ (türkisfarbig), $F_{- 35,77}$ (orangefarbig) und die Schnittkreismittelpunkte $M_{1}^{'}$ bzw. $M_{2}^{'}$ .

(Der deutlich sichtbare Punkt ist $M_{2}^{'}$ .)

Teilaufgabe 3

Berechnung der Tangentialebenengleichung $E_{2}$

Die Gleichung für eine Tangentialebene $E_{2}$ im Punkt $A$ der Kugel $K$ mit dem Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ lautet:

E_{2} : (\vec{x} - \vec{a}) \circ (\vec{a} - \vec{m}) = 0

Setze $A$ und $M$ in $E_{2}$ ein:

\begin{array}{rrccl} E_{2} : & (\vec{x} - (\begin{array}{c} 8 \\ 2 \\ - 1 \end{array})) & \circ ((\begin{array}{c} 8 \\ 2 \\ - 1 \end{array}) - (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array})) & = & 0 \\ (\vec{x} - (\begin{array}{c} 8 \\ 2 \\ - 1 \end{array})) & \circ (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) & = & 0 \end{array}

Das Skalarprodukt wird mit Hilfe des Distributivgesetzes ausmultipliziert:

\begin{array}{rcl} 6 x_{1} + 0 x_{2} + 0 x_{3} - (8 \cdot 6 + 2 \cdot 0 + (- 1) \cdot 0) & = & 0 \\ 6 x_{1} + 0 x_{2} + 0 x_{3} - (48 + 0 + 0) & = & 0 \\ 6 x_{1} - 48 & = & 0 \\ x_{1} & = & 8 \end{array}

Antwort: Die Gleichung für die Tangentialebene $E_{2}$ im Punkt $A$ der Kugel $K$ lautet: $x_{1} = 8$

Teilaufgabe 4

Berechnung der Schnittgeraden der Ebenen $E_{1}$ und $E_{2}$

\begin{array}{cccccccl} E_{1} : 4 x_{1} & + & 4 x_{2} & + & 2 x_{3} & = & - 22 & und \\ E_{2} : x_{1} & = & 8 \end{array}

Hier bietet sich das Einsetzungsverfahren an. Setze $x_{1} = 8$ in $E_{1}$ ein und löse nach $x_{2}$ auf:

\begin{array}{rcl} 4 \cdot 8 + 4 x_{2} + 2 x_{3} & = & - 22 \\ 32 + 4 x_{2} + 2 x_{3} & = & - 22 \\ 4 x_{2} + 2 x_{3} & = & - 54 \\ x_{2} & = & - 13,5 - 0,5 x_{3} \end{array}

Du hast nun $x_{2}$ in Abhängigkeit von $x_{3}$ dargestellt. Für $x_{3}$ kannst Du z. B. den Parameter $t$ setzen. Somit hat die Lösungsmenge des Gleichungssystems folgende Form:

𝕃 = {(8 | - 13,5 - 0,5 t | t) | t \in ℝ}

Mit Vektoren geschrieben sieht die Lösungsmenge folgendermaßen aus:

\vec{x} = (\begin{array}{c} 8 \\ - 13,5 - 0,5 t \\ t \end{array}) = (\begin{array}{c} 8 \\ - 13,5 \\ 0 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 0,5 \\ 1 \end{array})

Die Schnittgerade der beiden Ebenen lautet somit:

g (E_{1}, E_{2}) : \vec{x} = (\begin{array}{c} 8 \\ - 13,5 \\ 0 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 0,5 \\ 1 \end{array})

Erstelle nun die Geradengleichung $g$ auf der sich der Kugelmittelpunkt bewegt. Dazu liefert Dir die Geradengleichung $g (E_{1}, E_{2})$ den Richtungsvektor der Geraden $g$ . Der Stützvektor der Geraden $g$ ist der Vektor zum Kugelmittelpunkt.

Antwort: Die Gleichung der Geraden $g$ auf der sich der Kugelmittelpunkt bewegt lautet:

g : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 0,5 \\ 1 \end{array})

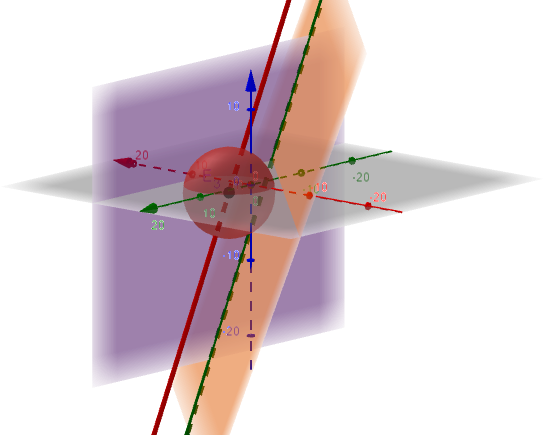
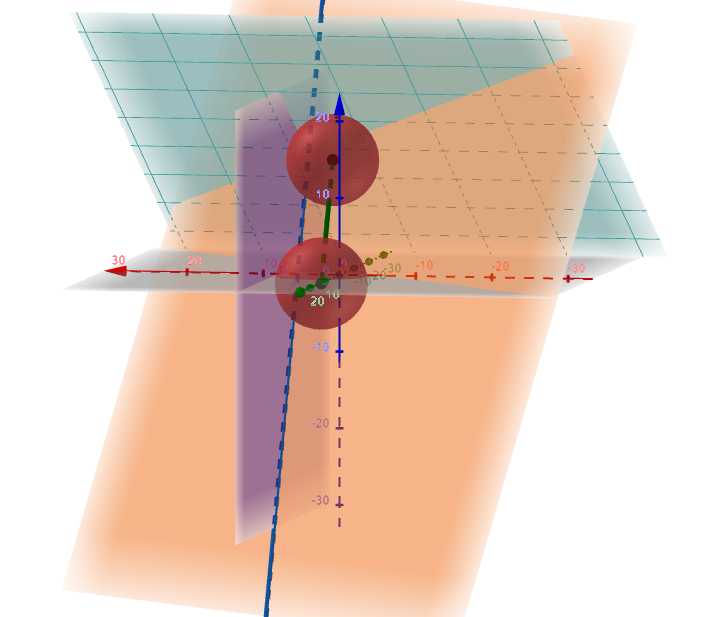
Die nebenstehende Abb. ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.

Dargestellt sind die Kugel $K$ , die Ebenen $E_{1}$ und $E_{2}$ , die Schnittgerade der beiden Ebenen (in grün) und die Gerade g auf der sich der Kugelmittelpunkt bewegt (in rot).

Teilaufgabe 5

Berechnung der Länge der Strecke, die die Kugel vom Startpunkt aus zurücklegt

Die nebenstehende Skizze zeigt Dir wie Du den zurückgelegten Weg berechnen kannst. Du berechnest den Abstand $d (M, E_{3})$ des Kugelmittelpunktes von der Ebene $E_{3}$ . Den zurückgelegten Weg $s$ findest Du als Differenz von $d (M, E_{3})$ und dem Kugelradius $r$ .

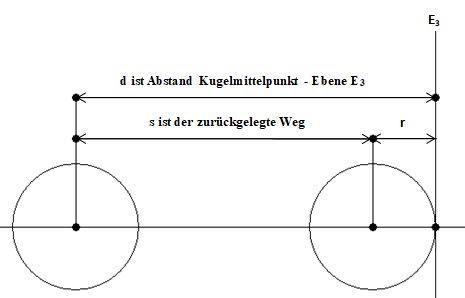
Für die Abstandsberechnung benötigst Du wieder die hessesche Normalenform der Ebene $E_{3}$ .

Der Normalenvektor der Ebene $E_{3}$ lautet:

\vec{n} = (\begin{array}{c} 0 \\ 2 \\ - 4 \end{array}) \Rightarrow | \vec{n} | = \sqrt{0^{2} + 2^{2} + (- 4)^{2}} = \sqrt{20}

Die Ebenengleichung $E_{3}$ in Koordinatenform wird durch den Betrag des Normalenvektors $| \vec{n} |$ geteilt und Du erhältst die hessesche Normalenform.

H N F : \frac{2 x_{2} - 4 x_{3} + 96}{\sqrt{20}} = 0

Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein:

\begin{array}{rcl} d (M, E_{3}) & = & | \frac{2 \cdot 2 - 4 \cdot (- 1) + 96}{\sqrt{20}} | \\ = & | \frac{104}{\sqrt{20}} | \\ = & 5,2 \cdot \sqrt{20} \end{array}

Für den zurückgelegten Weg gilt:

s = d (M, E_{3}) - r \Rightarrow s = 5,2 \cdot \sqrt{20} - 6 \approx 17,26

Antwort: Die Länge der Strecke $s$ , die die Kugel $K$ vom Startpunkt aus zurückgelegt hat, beträgt etwa 17,26.

Die nebenstehende Abb. ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.

Dargestellt sind die Kugel $K$ am Startpunkt und am Ende der zurückgelegten Strecke (in grün) , die Ebenen $E_{1}$ (orange), $E_{2}$ (lila) und $E_{3}$ (türkis) und die Schnittgerade (blau) der beiden Ebenen $E_{1}$ und $E_{2}$ .

Du kannst die Aufgabe mit folgender Strategie lösen:

Strategie zu Teilaufgabe 1

Berechne den Abstand des Kugelmittelpunktes von der Ebene $E_{1}$ . Dazu benötigst Du die hessesche Normalenform die Du aus der Koordinatenform der Ebene $E_{1}$ berechnen kannst. Setze den Kugelmittelpunkt $M$ in die hessesche Normalenform ein und Du erhältst den Abstand $d$ des Kugelmittelpunktes von der Ebene $E_{1}$ . Da $E_{1}$ Tangentialebene sein soll, muss der Abstand $d$ gleich dem Kugelradius $r = 6$ sein. Den Berührpunkt $B$ berechnest Du, indem Du die Lotgerade von $M$ auf die Ebene $E_{1}$ mit der Ebene $E_{1}$ schneidest.

Strategie zu Teilaufgabe 2

Du benötigst die hessesche Normalenform der Ebene $F_{a}$ . Berechne dann den Abstand des Kugelmittelpunktes $M$ von der Ebene $F_{a}$ . Um einen Schnittkreis zu erhalten muss dieser Abstand $d (M, F_{a})$ kleiner als der Kugelradius $r = 6$ sein.

Der Radius $r^{'}$ des Schnittkreises soll $2,2$ betragen. Der Satz von Pythagoras liefert die Bedingung für den Abstand $d$ des Kugelmittelpunktes zu $F_{a}$ . In die $H N F$ der Ebene $F_{a}$ setzt Du nun die Koordinaten des Kugelmittelpunktes ein und verlangst, dass der berechnete Abstand gleich dem Abstand $d$ ist. Nun kannst Du den Parameter $a$ berechnen.

Den Mittelpunkt $M^{'}$ des Schnittkreises berechnest Du indem Du die Lotgerade von $M$ auf die Ebene $F_{a}$ mit der Ebene $F_{a}$ schneidest. Beachte dabei, dass Du die beiden vorher erhaltenen Werte für den Parameter $a$ benutzt um zwei Schnittkreismittelpunkte zu berechnen.

Strategie zu Teilaufgabe 3

Setze den gegebenen Punkt $A$ in die Tangentialebenengleichung ein und Du erhältst die Ebenengleichung $E_{2}$ .

Strategie zu Teilaufgabe 4

Schneide die Ebenen $E_{1}$ und $E_{2}$ um die Schnittgerade zu berechnen. Für die Gleichung der Geraden $g$ auf der sich der Kugelmittelpunkt bewegt wählst Du als Stützvektor den Vektor zum Kugelmittelpunkt und als Richtungsvektor den Richtungsvektor der Schnittgeraden von $E_{1}$ und $E_{2}$ .

Strategie zu Teilaufgabe 5

Du benötigst die hessesche Normalenform der Ebene $E_{3}$ . Berechne dann den Abstand $d (M, E_{3})$ des Kugelmittelpunktes $M$ von der Ebene $E_{3}$ . Du berechnest die Länge der Strecke $s$ , die die Kugel $K$ vom Startpunkt aus zurückgelegt hat, als Differenz von $d (M, E_{3})$ und dem Kugelradius $r$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teilaufgabe 1

Bestimmung der Art des Schnitts von Ebene und Kugel

Berechnung des Berührpunktes B

Teilaufgabe 2

Bestimmung der hessischen Normalenform der Ebenenschar Fa

Bestimmung des Parameter a, so dass der Schnittkreisradius r=2,2 beträgt

Bestimmung des Mittelpunktes M′des Schnittkreises

Teilaufgabe 3

Berechnung der Tangentialebenengleichung E2

Teilaufgabe 4

Berechnung der Schnittgeraden der Ebenen E1 und E2

Teilaufgabe 5

Berechnung der Länge der Strecke, die die Kugel vom Startpunkt aus zurücklegt

Strategie zu Teilaufgabe 1

Strategie zu Teilaufgabe 2

Strategie zu Teilaufgabe 3

Strategie zu Teilaufgabe 4

Strategie zu Teilaufgabe 5

Berechnung des Berührpunktes $B$

Bestimmung der hessischen Normalenform der Ebenenschar $F_{a}$

Bestimmung des Parameter $a$ , so dass der Schnittkreisradius $r = 2,2$ beträgt

Bestimmung des Mittelpunktes $M^{'}$ des Schnittkreises

Berechnung der Tangentialebenengleichung $E_{2}$

Berechnung der Schnittgeraden der Ebenen $E_{1}$ und $E_{2}$