Gruppe A - lernen mit Serlo!

1

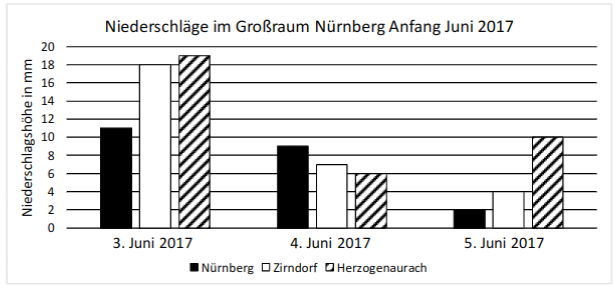
Das Diagramm zeigt die Niederschlagshöhen, die für drei aufeinanderfolgende Tage an den Messstellen in Nürnberg, Zirndorf und Herzogenaurach erfasst wurden.

Gib die Bedeutung des Wertes des Terms $19\ \text{mm}+\ 6\ \text{mm}\ +\ 10\ \text{mm}$ im Sachzusammenhang an.
Berechne aus den Daten des Diagramms den Mittelwert, der drei am 3. Juni 2017 gemessenen Niederschlagshöhen.
Die Fläche des Marktplatzes in Zirndorf beträgt etwa $2000\ \text{m}^2$ . Berechne mithilfe des Diagramms, wie viele $\text{m}^3$ Regen am 5. Juni 2017 in etwa auf den Marktplatz in Zirndorf fielen.

2

Die Abbildung zeigt ein gleichschenkliges Dreieck ABC mit Basis [AB] und $γ=50°$ . Der Mittelpunkt des abgebildeten Kreisbogens ist B .

Linda berechnet korrekt die Größe des Winkels $α$ mit dem Ansatz

\displaystyle α=\left(180°-γ\right):2

und erhält $α=65°$ .

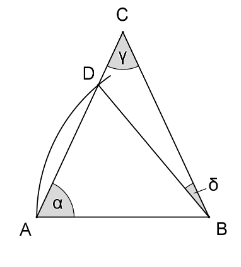
Gib die beiden mathematischen Zusammenhänge über Winkelgrößen an, die Lindas Ansatz zugrunde liegen.
Berechne die Größe des Winkels $δ$ .

3

Der Preis für ein Fahrrad wurde zweimal geändert und beträgt nun $352$ €. Die folgende Gleichung beschreibt diese Änderung: $x\cdot1{,}1\cdot0{,}8=352€$ .

Vervollständige: „Der Preis für das Fahrrad stieg bei der einen Änderung um __________ $%$ $\%$ $%$ und fiel bei der anderen Änderung um __________ $\%\$ ."

4

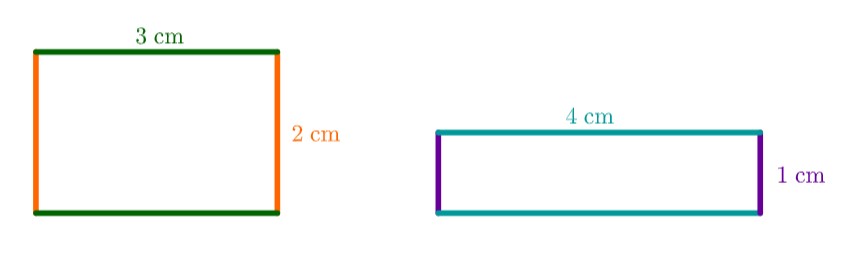
Begründe jeweils durch zeichnerische Darstellung eines Gegenbeispiels, dass die Aussage falsch ist. Beschrifte dabei deine Figuren geeignet.

Haben zwei Rechtecke den gleichen Flächeninhalt, so haben sie auch den gleichen Umfang.
- richtig
- falsch
Haben zwei Dreiecke den gleichen Umfang, dann sind sie kongruent.
- richtig
- falsch

5

Gegeben sind die beiden Terme

$T_1\left(x\right)=-3x^2+4x-1^{ }$ und

$T_2\left(x\right)=-3\left(x-\frac{1}{3}\right)\left(x-1\right)$ .

Berechne die Termwerte $T_1\left(0\right)$ und $T_2\left(0\right)$ .
Zeige, dass die beiden Terme zueinander äquivalent sind, indem du $T_2\left(x\right)$ geeignet umformst.
Gib zwei Terme $S_1\left(x\right)$ und $S_2\left(x\right)$ an, für die $S_1\left(0\right)=S_2\left(0\right)$ gilt, die aber nicht zueinander äquivalent sind.

6

Die Abbildung zeigt die Skulptur „Le Pouce“ (Der Daumen) in Paris. Sophie schätzt, dass die Höhe der Skulptur 200-mal so groß ist wie die Daumenlänge eines Menschen. Beurteile nachvollziehbar, ob ihre Abschätzung annehmbar ist.

7

Löse folgende Aufgaben.

Wähle vier aufeinanderfolgende natürliche Zahlen und prüfe, ob deren Summe durchvier teilbar¹ ist.
$^1$ Eine natürliche Zahl $a$ ist durch eine natürliche Zahl $b$ teilbar, wenn die Division „aufgeht“, d. h. der Wert von $a:b$ eine natürliche Zahl ist. Beispielsweise ist $4$ durch $2$ teilbar, aber nicht durch $3$ .
Zeige mithilfe einer allgemeinen Rechnung, dass die Summe von fünf beliebigen aufeinanderfolgenden natürlichen Zahlen stets durch fünf teilbar¹ ist.
$^1$ Eine natürliche Zahl $a$ ist durch eine natürliche Zahl $b$ teilbar, wenn die Division „aufgeht“, d. h. der Wert von $a:b$ eine natürliche Zahl ist. Beispielsweise ist 4 durch 2 teilbar, aber nicht durch 3.