Analysis, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion h: $x\mapsto x\cdot \ln(x²)$ mit maximalem Definitionsbereich $D_h$ .
1. Geben Sie $D_h$ an und zeigen Sie, dass für den Term der Ableitungsfunktion h′ von h gilt: $h'(x)=\ln(x²)+2$
2. Bestimmen Sie die $x$ -Koordinate des im II. Quadranten liegenden Hochpunkts des Graphen von $h$ .
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Abbildung 1 zeigt den Graphen $G_{f'}$ der Ableitungsfunktion f′ einer in $\mathbb{R}$ definierten ganzrationalen Funktion f. Nur in den Punkten $(-4|f'(-4))$ und $(5|f'(5)$ hat der Graph $G_{f'}$ waagrechte Tangenten.
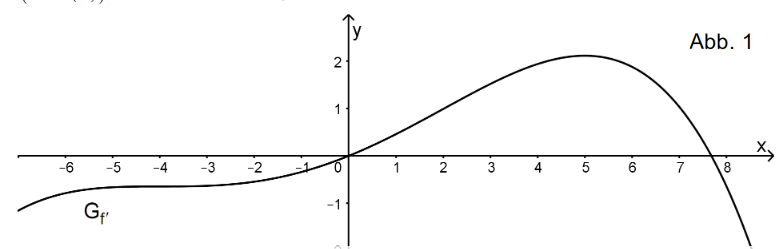
1. Begründen Sie, dass $f$ genau eine Wendestelle besitzt.
2. Es gibt Tangenten an den Graphen von f, die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermitteln Sie anhand des Graphen $G_{f'}$ der Ableitungsfunktion f′ in der Abbildung 1 Näherungswerte für die x-Koordinaten derjenigen Punkte, in denen der Graph von f jeweils eine solche Tangente hat
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben sind die in IR definierten Funktionen $f: x \mapsto x²+4$ und
$g_m: x \mapsto m\cdot x$ mit $m \in\mathbb{R}$ . Der Graph von f wird mit $G_f$ und der Graph von $g_m$ mit $G_m$ bezeichnet.
1. Skizzieren Sie $G_f$ in einem Koordinatensystem. Berechnen Sie die Koordinaten des gemeinsamen Punkts der Graphen $G_f$ und $G_4$ .
2. Es gibt Werte von m, für die die Graphen $G_f$ und $G_m$ jeweils keinen gemeinsamen Punkt haben. Geben Sie diese Werte von m an
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $g$ mit $g(x)$ = 0,7 $\cdot$ $e^{0{,}5x}$ - 0,7 und $x$ $\in\mathbb{R}.$
Die Funktion $g$ ist umkehrbar. Die Abbildung 2 zeigt den Graphen $G_g$ von $g$ sowie einen Teil des Graphen $G_h$ der Umkehrfunktion $h$ von $g$ .
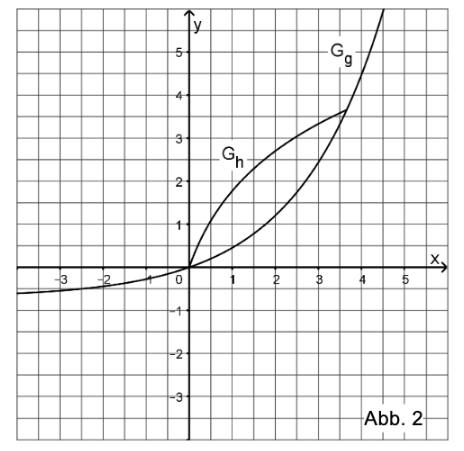
a) Zeichnen Sie in die Abbildung 2 den darin fehlenden Teil von $G_h$ ein.
b) Betrachtet wird das von den Graphen $G_g$ und $G_h$ eingeschlossene Flächenstück. Schraffieren Sie den Teil dieses Flächenstücks, dessen Inhalt mit dem Term
$2 \cdot \int_{0}^{2{,}5} (x-g(x)) \mathrm{d}x$ berechnet werden kann.
c) Geben Sie den Term einer Stammfunktion der in $\mathbb{R}$ definierten Funktion
k: x $\mapsto$ x - g(x) an.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?