Bruchterme durch Kürzen vereinfachen

1 Überblick

In diesem Kurs lernst du, wie du einen einzelnen Bruchterm so weit wie möglich kürzt und dadurch vereinfachst. Dabei wirst du Grundlagen im Umgang mit Termen brauchen. Keine Angst! Diese Grundlagen werden im Kurs nochmal wiederholt.

Trotzdem sind sie hier schon mal verlinkt:

Terme vereinfachen
Faktorisieren durch Ausklammern und binomische Formeln
Brüche kürzen

2 Grundlagen sind die halbe Miete

Es ist wieder mal $8$ Uhr morgens irgendwo in Deutschland. Deine Mathelehrerin hat schon angedeutet, dass ein neues Thema ansteht und euch dafür auch einiges an Grundwissen wiederholen lassen.

Doch als sie jetzt die Tafel aufklappt, traust du zunächst deinen Augen nicht:

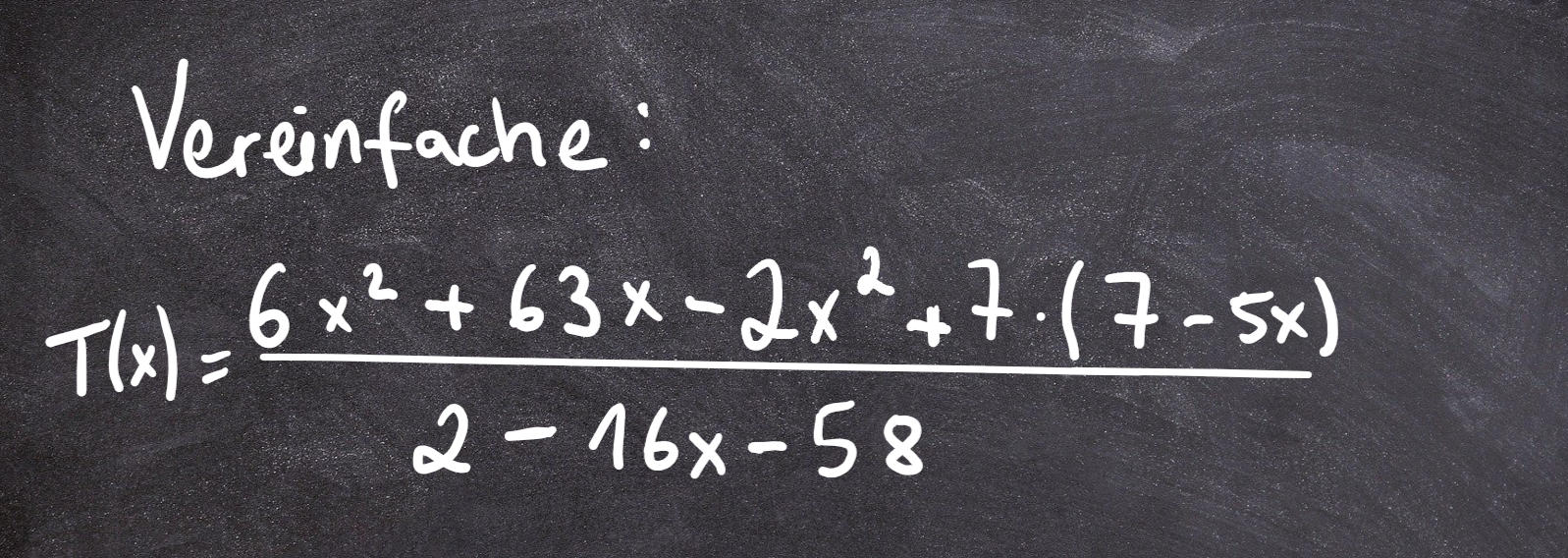
Sie beruhigt die Unruhe:

"Fast alles, was ihr braucht, könnt ihr schon. Dieser Term ist unser großes Ziel am Ende der Übungen. Und ich werde euch beweisen, dass es ganz einfach ist, wenn man Schritt für Schritt vorgeht."

3 Zähler und Nenner einzeln betrachten

Gleich zu Beginn ein wichtiger Tipp: Bis du der Meinung bist, dass Zähler und Nenner nicht mehr weiter bearbeitbar sind, betrachtest du Zähler und Nenner zunächst getrennt.

Da es aber ein gemeinsamer Term ist, musst du beim Schreiben in dein Heft natürlich trotzdem ordentlich arbeiten.

Da Termumformungen einen äquivalenten Term erzeugen, verbindest du deine einzelnen Vereinfachungen wie gewohnt durch ein Gleichheitszeichen:

4 Wiederholung: Terme vereinfachen I

Für die Wiederholung kannst du dir erstmal Beispiele ohne Bruchstriche anschauen. Diese Beispiele können dann aber genau so im Zähler oder Nenner eines Bruchterms stehen. Bist du dir unsicher bei dem Thema, schau dir am besten den ganzen Kurs Terme vereinfachen an.

Addieren und Subtrahieren

Achte darauf, die Variablen bei der Addition und Subtraktion richtig zu behandeln:

$\displaystyle T\left(x\right)$	$=$	$\displaystyle 2x^2-4x+7+3x-xy-2x^2\$
	↓	Du kannst durch das Kommutativgesetz den Term sortieren. Gleiche Variablen mit gleichen Exponenten bringst du zueinander.
	$=$	$\displaystyle 2x^2-2x^2-4x+3x+7-xy\$
	↓	Addieren und Subtrahieren kann man nur, wenn die Variable exakt gleich vorkommt
	$=$	$\displaystyle -1x+7-xy$

5 Wiederholung: Terme vereinfachen II

Neben Addieren und Subtrahieren kannst du auch Multiplizieren und Dividieren

Multiplizieren und Dividieren ohne Klammern

Hier passiert leicht der Fehler, dass mehr als einmal multipliziert oder dividiert wird. Schreibst du dir (gedanklich) die weggelassenen Rechenzeichen dazu, sollte dies aber leicht zu vermeiden sein:

$\displaystyle T\left(x\right)$	$=$	$\displaystyle 12\cdot x\ \cdot2\cdot x$
	↓	Hier gilt wieder das Kommutativgesetz.
	$=$	$\displaystyle 12\cdot2\cdot x\ \cdot x$
	↓	Dann wird Zahl mit Zahl und $x$ mit $x$ verrechnet.
	$=$	$\displaystyle 24x^2$

6 Wiederholung: Terme vereinfachen III

Kommen Klammern vor, so solltest du diese häufig (nicht immer!) ausmultiplizieren, damit du einen guten Überblick über die Terme bekommst.

Das gilt vor allem, wenn außerhalb der Klammern noch Summen oder Differenzen gebildet werden.

Häufig helfen Bögen über den Bestandteilen, um besser nachzuvollziehen, was du bereits multipliziert hast:

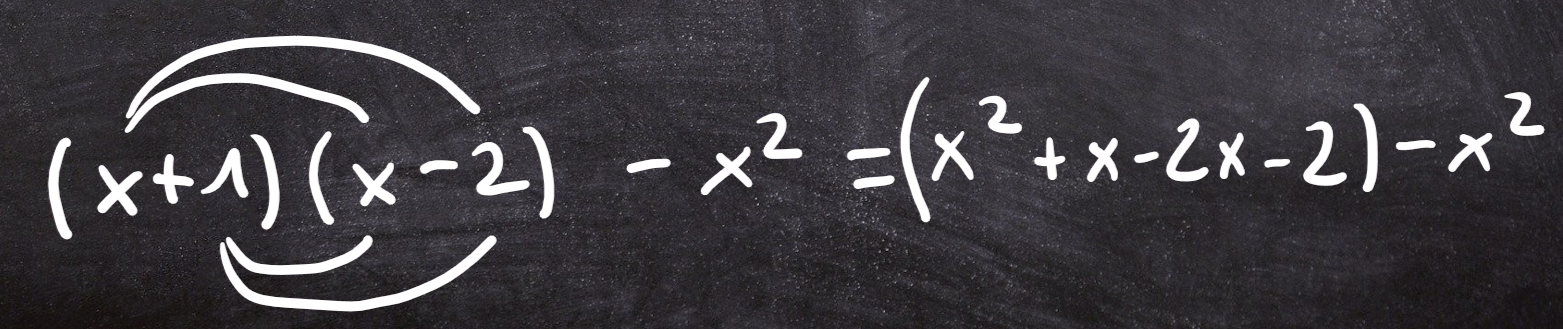
Im allgemeinen Wegweiser zum Umgang mit Klammern findest du nochmal ausführliche Erklärungen und Tipps.

7 Übung zur Wiederholung: Terme

Vereinfache so weit wie möglich!

Laden

Es gibt zur Übung auch noch weitere Aufgaben zu Summentermen und Ausmultiplizieren

8 Wiederholung: Brüche kürzen

Ein Bruchterm ist erstmal nur ein Bruch, bei dem (im Zähler und) im Nenner zusätzlich Variablen vorkommen. Deshalb sollten doch Methoden, die du für Brüche gelernt hast, auch für Bruchterme anwendbar sein, oder?

Ja! Und genau das ist auch dein Ziel. Ähnlich, wie du bereits Brüche gekürzt hast, kannst du auch Bruchterme kürzen.

Dafür musst du dich aber zuerst erinnern, wie Brüche eigentlich gekürzt wurden.

Dafür kannst du den Bruch $\frac{36}{189}$ genauer unter die Lupe nehmen.

Zerlegung in Primfaktoren

Finde möglichst kleine Faktoren für die Zahlen in Nenner und Zähler:

\displaystyle \frac{36}{189}=\ \frac{3\cdot3\cdot2\cdot2}{3\cdot3\cdot3\cdot7}

Beim Kürzen kannst du alles streichen, was sowohl beim Produkt des Zählers als auch beim Produkt des Nenners vorkommt. Im Zähler ist zum Beispiel zweimal die 3, im Nenner auch, deshalb darf man sie zweimal wegstreichen. Die letzte 3 im Nenner muss stehen bleiben:

\displaystyle \frac{\cancel{3}\cdot\cancel{3}\cdot2\cdot2}{\cancel{3}\cdot\cancel{3}\cdot3\cdot7}= \dfrac{2\cdot 2}{3\cdot 7}=\dfrac 4 {21}

9 Übung zur Wiederholung: Kürzen

Kürze den Bruch so weit wie möglich:

Laden

10 Unterschiede Bruch und Bruchterm

Was sind die wichtigsten Unterschiede zwischen dem Bruch $\frac{30}{210}$ und dem Bruchterm $\frac{6}{x+3}$ ?

Zum einen kommt natürlich eine Variable im Nenner vor, denn sonst wäre es kein Bruchterm.

Außerdem passiert aber auch etwas, dass bei einem normalen Bruch nicht passieren kann: Obwohl Zähler und Nenner nicht mehr weiter vereinfacht werden können, stehen im Bruchterm noch Rechenzeichen!

Das erschwert das Kürzen, denn: Weggestrichen werden dürfen nur Faktoren, die in einem Produkt sowohl im Zähler als auch im Nenner vorkommen. Oder salopp gesagt:

In Differenzen und in Summen kürzen nur die Dummen!

11 Aus Bruchtermen mit Produkten kürzen

Bestehen Zähler und Nenner jeweils aus Produkten, so kann wie bei den Brüchen gleiches gekürzt werden:

$\displaystyle T\left(x\right)$	$=$	$\displaystyle \frac{12x^2}{9x}$
	↓	Zerlege in Primfaktoren
	$=$	$\displaystyle \frac{2\cdot2\cdot3\cdot x\cdot x}{3\cdot3\cdot x}$
	↓	Markiere, was sowohl im Zählerprodukt als auch im Nennerprodukt vorkommt
	$=$	$\displaystyle \frac{2\cdot2\cdot\cancel{3}\cdot \cancel{x}\cdot x}{\cancel{3}\cdot3\cdot \cancel{x}}$
	↓	Kürze, was sowohl im Zählerprodukt als auch im Nennerprodukt vorkommt
	$=$	$\displaystyle \frac{4x}{3}$

Auch das ist schon eine kurze Übung wert!

12 Übung zum Kürzen bei Produkten

Laden

13 Wiederholung: Faktorisieren I

Aber was, wenn im Bruchterm kein Produkt steht sondern Summen oder Differenzen?

Auch dafür kennst du bereits ein Werkzeug: Das Faktorisieren

Ausklammern

Eine Möglichkeit zu faktorisieren ist es, Bestandteile, die in jedem Summanden vorkommen, auszuklammern. Wie der Name schon sagt, wird dabei etwas herausgenommen und etwas in Klammern gesetzt:

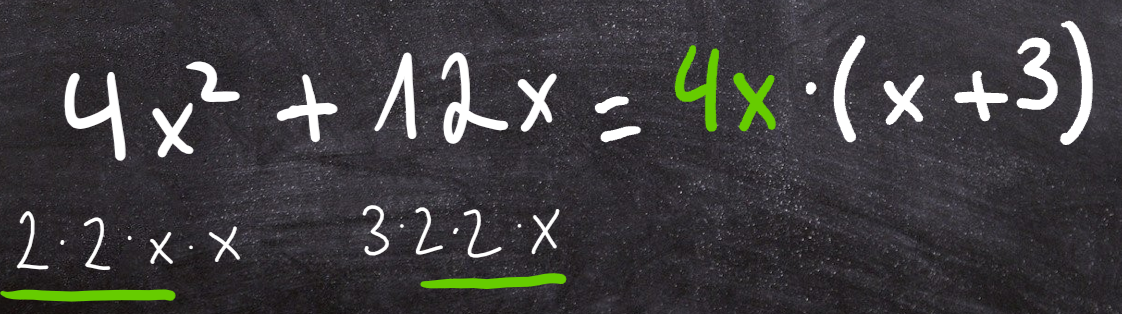
Wichtig: Multipliziert man zur Probe wieder aus, so muss wieder das Gleiche dastehen wie zuvor!

Häufig ist zum Beispiel der Summand $1$ schnell vergessen, wenn ein Summand komplett ausgeklammert werden kann:

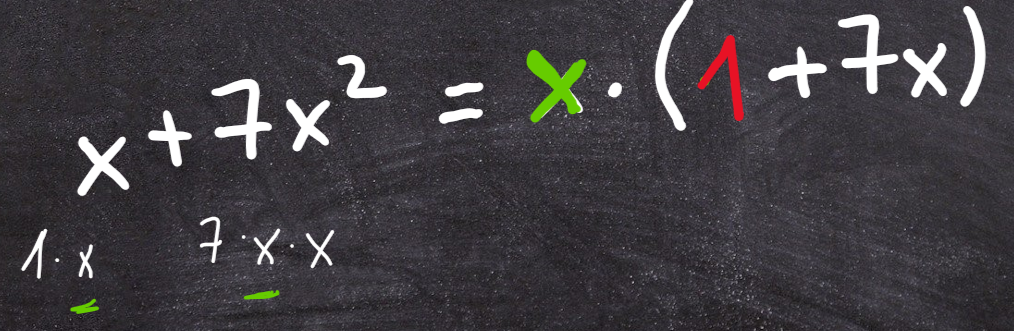
14 Übungen zum Ausklammern

Klammere aus

Laden

Was fehlt in der Klammer?

Laden

Klammere den Ausdruck aus der Klammer aus

Laden

Weitere Übungen gibt es im Ordner Aufgaben zum Ausklammern

15 Wiederholung: Faktorisieren II

Schau dir diesen Term einmal ganz genau an und überlege, was dir auffällt:

\displaystyle x^2+6x+9

16 Binomische Formel rückwärts

Jetzt hast du dir die binomischen Formeln vielleicht gerade vorwärts gemerkt und jetzt sollst du sie wieder rückwärts anwenden?

Ja, denn sie helfen dir, Summenterme, die eine ganz bestimmte Form haben, wieder in ein Produkt zu verwandeln!

Dabei sollten dich vor allem Quadrate hellhörig werden lassen, denn jede ausmultiplizierte binomische Formel hat immer zwei Bestandteile, die ein Quadrat sind:

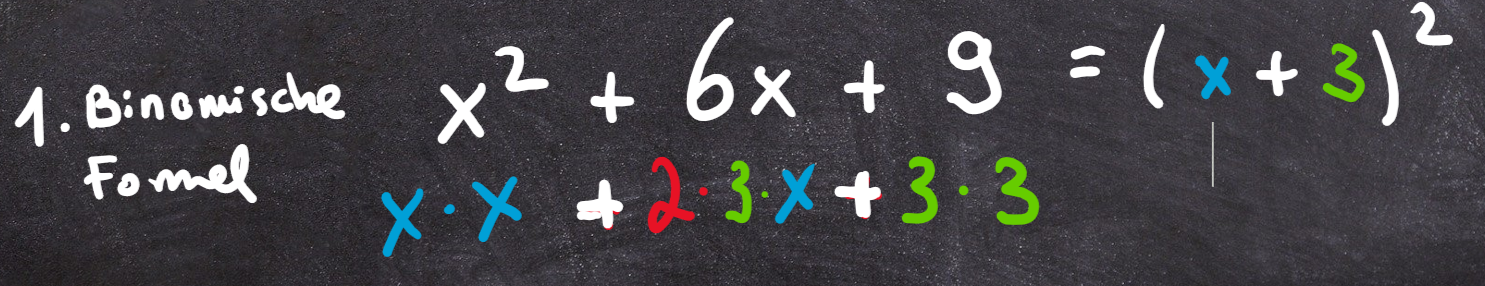
Bei der 1. Binomischen Formel wird zusätzlich zu den Quadraten noch das Doppelte der gesuchten Zahlen addiert, bei der zweiten wird es subtrahiert und die dritte binomische Formel ist die schönste Formel: Hier werden die Quadrate voneinander abgezogen und es gibt keinen weiteren Baustein!

Hat man eine binomische Formel in einem Bruchterm entdeckt, lässt sich diese sofort in die faktorisierte Form $\left(a+b\right)^2,\left(a-b\right)^2$ oder $\left(a+b\right)\left(a-b\right)$ umschreiben.

Übung macht den Meister!

17 Übung binomische Formel rückwärts

Laden

18 Bruchterme kürzen

Es ist viel Handwerkszeug, aber jetzt hast du es geschafft!

Du kannst prinzipiell jeden Bruchterm, den dir die Welt entgegenwirft, durch gute Vorarbeit so weit wie möglich kürzen. Es bedarf nur einiger Übung und guter Konzentration.

Lies dir deshalb vor dem Üben nochmal dieses Beispiel durch und versuche nachzuvollziehen, was als nächstes passiert:

$\displaystyle T\left(x\right)$	$=$	$\displaystyle \frac{8x\ -2x\left(20-8x\right)}{x^2-4x+4}$
	↓	Zunächst vereinfachst du den Term im Zähler, indem du die Klammer ausmultiplizierst (da außerhalb noch eine Differenz ist, ist dies sinnvoll).
	$=$	$\displaystyle \frac{8x\ -40x+16x^2}{x^2-4x+4}$
	↓	Verrechne im Zähler. Ordne nach absteigender Potenz von x (bringt besseren Überblick).
	$=$	$\displaystyle \frac{16x^2-32x}{x^2-4x+4}$
	↓	Zerlege die Bestandteile der Summenterme von Zähler und Nenner in möglichst kleine Faktoren.
	$=$	$\displaystyle \frac{2\cdot2\cdot2\cdot2\cdot x\cdot x-2\cdot2\cdot2\cdot2\cdot2\cdot x}{x\cdot x-2\cdot2\cdot x+2\cdot2}$
	↓	Zähler: Finde den größtmöglichen Faktor zum Ausklammern.
	$=$	$\displaystyle \frac{\color{red}2\cdot2\cdot2\cdot2\cdot x\color{black}\cdot x-\color{red}2\cdot2\cdot2\cdot2\color{black}\cdot2\cdot\color{red} x}{x\cdot x-2\cdot2\cdot x+2\cdot2}$
	↓	Du kannst alles Rote ausklammern, da es in beiden Faktoren vorkommt. Insgesamt also $16 x$ .
	$=$	$\displaystyle \frac{16x\left(x-2\right)}{x\cdot x-2\cdot2\cdot x+2\cdot2}$
	↓	Im Nenner entdeckst du zwei Quadrate, einmal von $x$ und einmal von der $2$ . In der Mitte ist das Doppelte von $2 x$ . Es handelt sich also um eine binomische Formel. Aufgrund des Minus-Zeichens handelt es sich um die $2$ . binomische Formel.
	$=$	$\displaystyle \frac{16x\left(x-2\right)}{\left(x-2\right)^2}$
	↓	Der Faktor $(x - 2)$ kommt sowohl im Zähler als auch im Nenner vor.
	$=$	$\displaystyle \frac{16x\color{red}\left(x-2\right)}{\left(x-2\right)\color{red}\left(x-2\right)}$
	↓	Kürze den Faktor $(x - 2)$ .
	$=$	$\displaystyle \frac{16x}{x-2}$
	↓	(Die Klammern im Nenner sind optional)

19 Übungen Bruchterme kürzen

Laden

20 Zusammenfassung

Und? Traust du dich jetzt an die Aufgabe aus dem Unterricht heran?

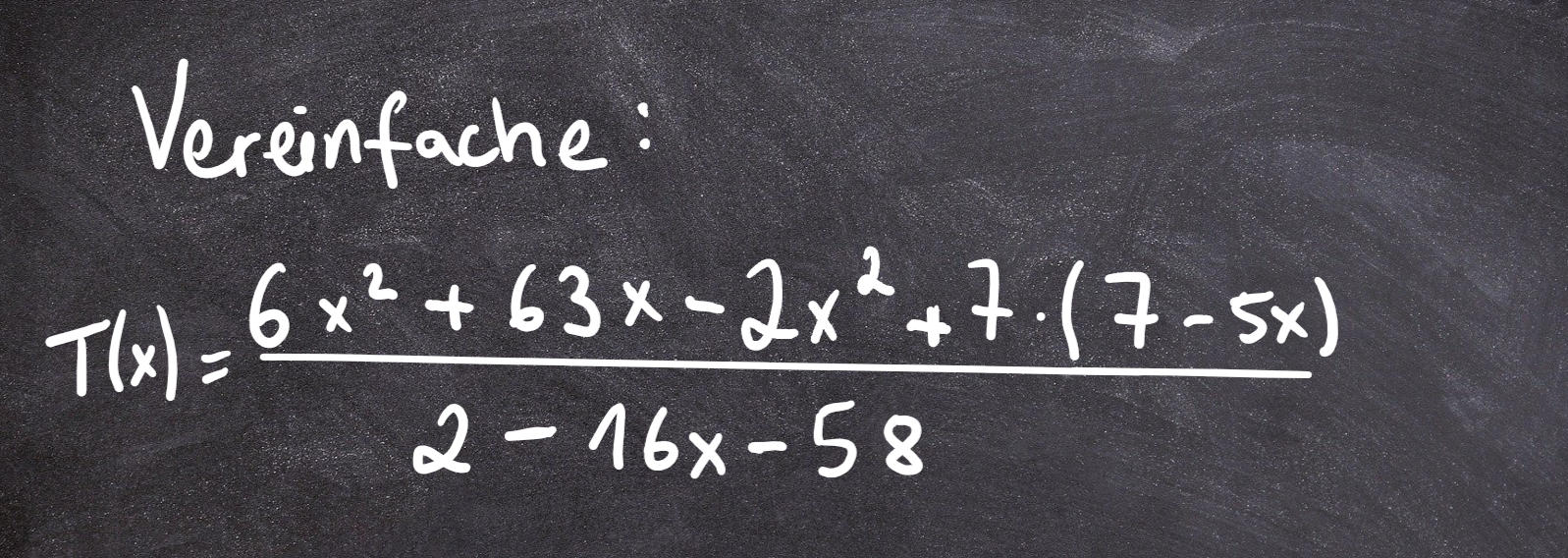
Wenn du dein Grundwissen parat hast, ist diese Aufgabe sicher auch eine leichte Übung für dich!

Grob gehst du immer gleich vor

Falls Zähler oder Nenner Summenterme sind (Außerhalb von Klammern sind Additionen/Subtraktionen) :

Terme vereinfachen und Klammern auflösen
Faktorisieren durch Ausklammern oder Binomische Formeln rückwärts
Möglichst große Faktoren kürzen (auch identische Klammern können gekürzt werden!)

Hast du zu Beginn bereits Produkte im Zähler und im Nenner (Keine Additionen/Subtraktionen außerhalb der Klammer), so lohnt es sich sicher, frühzeitig zu kürzen, falls dies möglich ist.