In diesem Kurs sind verschiedene Methoden zum Vereinfachen von Termen kurz umrissen. Er dient dabei mehr dazu, einen Überblick über die Methoden zu schaffen, als im Detail jeden Schritt zu erläutern.

Mithilfe von Verlinkungen kannst du entdeckte Lücken wie immer gut schließen.

Vorkenntnisse:

• Potenzen und Potenzgesetze

• Ausmultiplizieren von Klammern

• Verwendung von binomischen Formeln

• Rechnen mit Brüchen

Dauer:

Morgens, 8 Uhr in Deutschland. Verschlafen setzt du dich nach der Begrüßung der Lehrerin auf den Stuhl. Noch bevor du einen herzhaften Gähner ausstoßen kannst, klappt sie die Tafel auf und du siehst das:

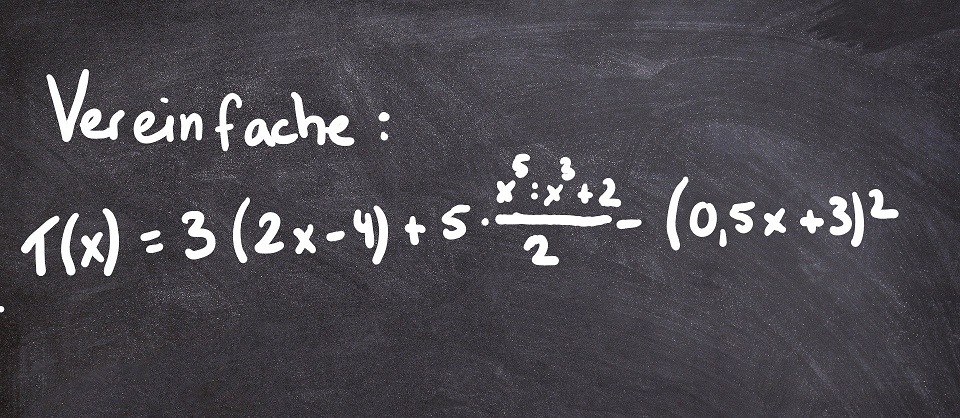
Selbst, wenn du in den letzten Wochen alles verstanden hättest: Wo sollst du hier überhaupt anfangen? Und wie vermeidest du häufige Fehler?

Keine Panik! In diesem Kurs wiederholst du nochmal wichtige Konzepte, die dir beim Vereinfachen von Termen helfen.

Wenn in deinem Rechenheft auf einmal Buchstaben stehen, hast du es sehr wahrscheinlich mit Variablen zu tun. Für die Verrechnung dieser Buchstaben miteinander gibt es ein paar einfache Regeln zum Zusammenfassen von Termen und Rechnen mit Potenzen:

unterschiedliche Variablen nicht verrechnen:

• $x-y=x-yx-y=x-y$ oder

• $2x\cdot 3y=2\cdot 3\cdot x\cdot y=6xy2x\backslash cdot3y\backslash \; =2\backslash cdot3\backslash cdot\; x\backslash cdot\; y=6xy$

Strichrechnungen bei gleichen Variablen nur bei gleicher Potenz, Exponent bleibt gleich:

• $3x^3-x^3=2x^{3}3x^3-x^3=2x^3$ aber

• $x^2+2x=x^2+2xx^2+2x=x^2+2x$

Multiplikation gleicher Variablen führt zur Addition der Exponenten:

• $x^2\cdot x^3=x^{2+3}=x^{5}x^2\backslash cdot\; x^3=x^\{2+3\}=x^5$ oder

• ${\left(a^3\right)}^2=a^3\cdot a^3=a^{2\cdot 3}=a^6\backslash left(a^3\backslash right)^2=a^3\backslash cdot\; a^3=a^\{2\backslash cdot3\}=a^6$

• Division gleicher Variablen führt zur Subtraktion der Exponenten:

  • $5a^4:a^2=5a^{4-2}=5a^{2}5a^4:a^2=5a^\{4-2\}=5a^2$ oder

  • $\frac{4y^7}{y^3}=4y^4\backslash frac\{4y^7\}\{y^3\}=4y^4$

Bei der Multiplikation mit Klammern ist höchste Konzentration gefordert: Bedenke beim Multiplizieren mehrerer Klammern, dass jeder Teil der ersten Klammer mit jedem der zweiten Klammer multipliziert werden muss und achte in jedem Fall darauf, dass du die Klammern nicht zu früh weglässt, da es noch weitere Punktrechnungen oder negative Vorzeichen vor der Klammer geben kann (Wegweiser zum Umgang mit Klammern).

Beispiele

Zahl mit Klammer:

$3\cdot (4x-3)=12x-9_{}3\backslash cdot\backslash left(4x-3\backslash right)=12x-9\_\{\; \}$

Klammer mit Klammer:

$(x^2-2)(2x+5)\backslash left(x^2-2\backslash right)\backslash left(2x+5\backslash right)$

$=x^2\cdot 2x+x^2\cdot 5-2\cdot 2x-2\cdot 5=x^2\backslash cdot2x+x^2\backslash cdot5-2\backslash cdot2x-2\backslash cdot5$

$=2x^3+5x^2-4x-10=2x^3+5x^2-4x-10$

Achtung! Mehrere Punktrechnungen:

$2\cdot (4x+8):4=(8x+16):4=2x+42\backslash cdot\backslash left(4x+8\backslash right):4=\backslash left(8x+16\backslash right):4=2x+4$

Achtung! Minus vor der Klammer:

$1-(33x^2+27):301-\backslash left(33x^2+27\backslash right):30\backslash$

$=1-(\mathrm{1,1}{x}^2+\mathrm{0,9})=1-\backslash left(1\{,\}1x^2+0\{,\}9\backslash right)$

$=1-\mathrm{1,1}{x}^2-\mathrm{0,9}=\mathrm{0,1}-\mathrm{1,1}{x}^2=1-1\{,\}1x^2-0\{,\}9=0\{,\}1-1\{,\}1x^2$

Ein Spezialfall beim Auflösen von Klammern sind die binomischen Formeln. Merkt man sich diese, so kann man einige Rechnungen schneller ausführen und muss weniger Angst vor Fehlern haben. Erneut sollte man darauf achten, die Klammern nicht zu früh wegzulassen!

Beispiele

Beispiel 1

${(x-7)}^2=x^2-2\cdot x\cdot 7+7^2=x^2-14x+49\backslash left(x-7\backslash right)^2=x^2-2\backslash cdot\; x\backslash cdot7+7^2=x^2-14x+49$

Beispiel 2

${(3x+3)}^2={\left(3x\right)}^2+2\cdot 3x\cdot 3+3^2=9x^2+18x+9\backslash left(3x+3\backslash right)^2=\backslash left(3x\backslash right)^2+2\backslash cdot3x\backslash cdot3+3^2=9x^2+18x+9$

Beispiel 3

$-{(x+1)}^2=-(x^2+2\cdot 1\cdot x+1^2)-\backslash left(x+1\backslash right)^2=-\backslash left(x^2+2\backslash cdot1\backslash cdot\; x+1^2\backslash right)$

$=-(x^2+2x+1)=-x^2-2x-1=-\backslash left(x^2+2x+1\backslash right)=-x^2-2x-1$

In Termen können auch Brüche mit Variablen im Zähler* vorkommen. Der häufigste Fehler beim Rechnen mit diesen Brüchen ist, dass man den Zähler und den Nenner nicht als eigene, eigentlich geklammerte Pakete sieht.

Der Term $\frac{x+5}{2}\backslash frac\{x+5\}\{2\}$ sollte eigentlich so geschrieben werden: $\frac{(x+5)}{\left(2\right)}\backslash frac\{\backslash left(x+5\backslash right)\}\{\backslash left(2\backslash right)\}$

Während die untere Klammer nicht zu Problemen führt, ist die obere sehr wichtig! Es gelten die gleichen Regeln wie beim Rechnen mit Brüchen:

$5\cdot \frac{(x+5)}{2}=\frac{5}{1}\cdot \frac{(x+5)}{2}=\frac{5(x+5)}{2}=\frac{5x+25}{2}5\backslash cdot\backslash frac\{\backslash left(x+5\backslash right)\}\{2\}=\backslash frac\{5\}\{1\}\backslash cdot\backslash frac\{\backslash left(x+5\backslash right)\}\{2\}=\backslash frac\{5\backslash left(x+5\backslash right)\}\{2\}=\backslash frac\{5x+25\}\{2\}$

Außerdem vergisst man schnell, dass Brüche eine andere Schreibweise für eine Division sind. Der Term $\frac{16x+8}{4}\backslash frac\{16x+8\}\{4\}$ kann ebenfalls so geschrieben werden: $(16x+8):4\backslash left(16x+8\backslash right):4$

Diese Division lässt sich dann wie gewohnt ausführen. Aber die Klammern erneut nicht zu früh weglassen:

$-\frac{121x+33}{11}=-(121x+33):11=-(11x+3)=-11x-3-\backslash frac\{121x+33\}\{11\}=-\backslash left(121x+33\backslash right):11=-\backslash left(11x+3\backslash right)=-11x-3$

*Kommt die Variable im Nenner vor, handelt es sich um einen Bruchterm. Dazu gibt es ein eigenes Kapitel auf Serlo!

Wenn du einen langen Term vor dir hast und gar nicht wirklich weißt, wo du anfangen sollst, hilft dir die KlaPoPS-Regel weiter:

Behalte dabei die Klammern immer so lang, bis du die Punktrechnungen ausgeführt hast, da sonst leicht Fehler passieren können.

Beispiel

Nun hast du alles, was du brauchst, um die Aufgabe zu lösen!

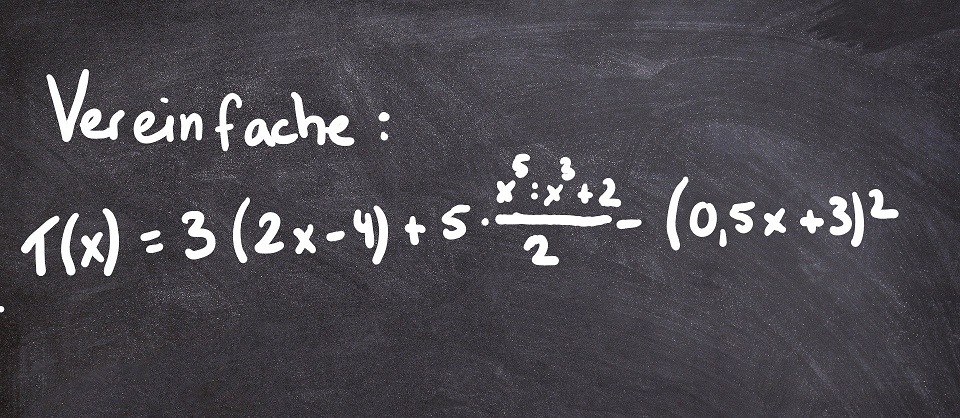
Noch einmal gemeinsam ran ans Werk. Konzentration ist der Schlüssel!