1 Startseite
Ziele
Dieser Kurs erklärt dir schrittweise die Vorgehensweise bei der quadratischen Ergänzung und wofür du sie verwenden kannst.
Voraussetzungen
Um Unklarheiten im Verlauf des Kurses zu vermeiden, solltest du dich in folgenden Themen bereits auskennen:
Wie sieht eine Parabel aus?
Du kannst den Kurs auch gleich starten und bei etwaigen Problemen den Links auf den jeweiligen Seiten folgen.
Viel Spaß beim Lernen und Üben!
2 Binomische Formeln
1. und 2. Binomische Formel
Um quadratische Ergänzung zu verstehen und anwenden zu können, musst du dich gut mit der 1. und 2. binomischen Formel auskennen.
Falls du denkst, dass du in dem Bereich fit bist, kannst du schon auf die nächste Seite gehen.
Falls du lieber noch eine kleine Wiederholung in diesem Bereich haben möchtest, dann bleib auf dieser Seite.
Die binomischen Formeln sind einfache Umformungen von quadratischen Termen. Diese lauten:
1. binomische Formel:
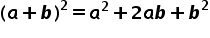
2. binomische Formel:
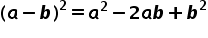
Von der linken Seite der Gleichung kommst du durch einfaches Ausmultiplizieren auf die rechte Seite der Gleichung. Von rechts nach links musst du eine Faktorisierung durchführen.
Ganz zentral für die quadratische Ergänzung ist die Rückrichtung, also das Faktorisieren. Zu diesem Bereich kannst du unten einige Übungsaufgaben bearbeiten.
(Weitere Erklärungen und Übungen findest du auch im Kurs und im Artikel binomische Formeln.)
Aufgabe 1
Faktorisiere den Term
Hier wird noch einmal erklärt, wie du vorgehen musst.
Aufgabe 2
Faktorisiere den Term
Auch hier noch einmal eine Erklärung, wie du vorgehen musst.
3 Einführung der quadratischen Ergänzung an einem Beispiel
Unten wird dir anhand eines Beispiels in allgemeiner Parabelform, nämlich , gezeigt, wie quadratische Ergänzung funktioniert.
Zuerst wird kurz beschrieben, was in diesem Schritt gemacht wird. Daneben siehst du, welchen Termbestandteil man betrachtet. In der letzten Spalte findest du abschließend den gesamten Term nach der Umformung.
Ziel ist es, die quadratische Funktion in Scheitelpunktsform zu erhalten.
Vorgehensweise | Beispiel | |
|---|---|---|
Womit wird etwas gemacht? | Was wurde gemacht? | |
Sortieren: Vorne der -Term, dann der -Term und dann die Konstante. Hier: nach vorne bringen. | ||
Ausklammern: Den Koeffizienten des quadratischen Terms bei den "x-Termen" ausklammern (Faktorisieren). Hier: bei den -Termen ausklammern. | ||
Ergänzen: Nun wollen wir eine binomische Formel erzeugen. Dafür fehlt noch der zweite Quadratterm. Halbiere den Vorfaktor des Terms mit und quadriere ihn. Das ist der benötigte Quadratterm. Addiere diesen Term, um die binomische Formel zu vervollständigen, und subtrahiere ihn direkt nochmal, um die Gleichung nicht zu verändern. Hier: Ergänzen mit | ändert nichts an der Gleichung da | |
Zusammenfassen: Mithilfe der binomischen Formeln. Hier: Der Term ist eine aufgelöste erste binomische Formel. | ||
Klammer ausmultiplizieren Hier: In der Klammer stehen die beiden Summanden und . | ||
Rechte Summe ausrechnen | ||
Am Ende erhält man die Scheitelform |
4 Allgemeine Vorgehensweise
Falls du noch sehen möchtest, wie die quadratische Ergänzung mit allgemeinen Parametern , und funktioniert, dann lies die unten stehende Tabelle.
Falls dir schon klar ist, wie du vorgehen musst, kannst du diese Seite auch überspringen.
In der Tabelle siehst du nochmals die Vorgehensweise erläutert anhand eines Beispiels und daneben allgemein mit den Parametern , und . In diesem Beispiel gilt: , und .
Schritt | Beispiel | Allgemein |
|---|---|---|
Sortieren: Vorne der -Term, dann der -Term und dann die Konstante. Hier: in die Mitte schieben | ||
Ausklammern: Den Koeffizienten des quadratischen Terms bei den "x-Termen" ausklammern (Faktorisieren). Hier: bei den -Termen ausklammern. | ||
Ergänzen: Halbiere den Vorfaktor des Terms mit , quadriere dann und addiere das Ergebnis direkt dahinter und subtrahiere es wieder. Hier: Ergänzen mit | ||
Zusammenfassen: mit Hilfe der Binomischen Formeln. Hier: Man kann den Term in eine binomische Formel umwandeln: | ||
Klammer ausmultiplizieren Hier: In der Klammer stehen die beiden Summanden und . | ||
Rechte Summe ausrechnen | ||
Am Ende erhält man die Scheitelform |
5 Übungsaufgaben
Laden
Laden
Laden
Laden
Laden
Laden
6 Sonderfall b=0
Neben der allgemeinen Form gibt es Funktionsterme der Form , bei denen ist.
Bei diesem Sonderfall ist die Scheitelform bereits gegeben, denn mit den Parametern , .
7 Anwendung: Scheitelpunkt bestimmen
Die allgemeine Form einer quadratischen Funktion lautet .
Oft musst du aus solchen Funktionstermen den Scheitel der zugehörigen Parabel ablesen. Der Scheitelpunkt ist die Extremstelle der Parabel, die zu der Funktion gehört. Das ist aber gar nicht so einfach.
Durch die quadratische Ergänzung hat man die Möglichkeit, den Term einer quadratischen Funktion, die in allgemeiner Parabelform notiert ist, in die Scheitelpunktsform umzuformen.
Die Scheitelpunktsform lautet:
Diese Form hat den Vorteil, dass man den Scheitelpunkt direkt aus ihr ablesen kann. Seine Koordinaten sind nämlich immer .
Beispiel 1
,
Scheitelpunkt:
Beispiel 2
,
Scheitelpunkt:
Beispiel 3
;
Scheitelpunkt:
8 Übungsaufgaben
Bestimme den Scheitelpunkt der folgenden Funktionen:
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
Aufgabe 4
Laden
Aufgabe 5
Laden
Aufgabe 6
Laden
Aufgabe 7
Laden
9 Anwendung: Lösen quadratischer Gleichungen
Eine normale quadratische Gleichung der Form kann man nicht ohne Weiteres lösen, da die gesuchte Variable sowohl im Quadrat , als auch linear vorkommt. In der Scheitelform ist dieses Problem behoben. Die Variable steht nur einmal in der binomischen Formel und die Gleichung ist durch Ziehen der Wurzel und einfaches Umformen der Gleichung lösbar.
Hier siehst du vier Beispiele für den Lösungsweg durch Wurzelziehen, bei denen links bereits eine Scheitelform steht.
Der Definitionsbereich ist jeweils .
Beispiel:
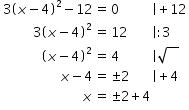
Beispiel:
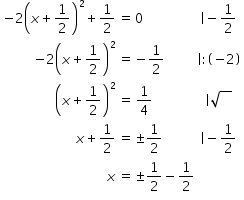
Beispiel:
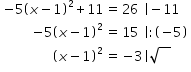
Wurzel aus ist nicht definiert.
keine Lösung
Beispiel:
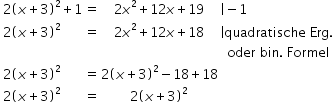
Allgemeingültige Aussage
Lösungsmenge entspricht der Definitionsmenge
Das Lösen einer quadratischen Gleichung ist auch anders, z.B. mit der Mitternachtsformel, möglich. Später wirst du noch sehen, dass die Mitternachtsformel nur eine allgemeine Anwendung der quadratischen Ergänzung ist.
10 Übungsaufgaben
Löse die folgenden quadratischen Gleichungen mit quadratischer Ergänzung.
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
Aufgabe 4
Laden
Aufgabe 5
Laden
11 Exkurs: Quadratische Ergänzung und Mitternachtsformel
Die Mitternachtsformel ist ein einfaches Mittel, um quadratische Gleichungen zu lösen. Aber man setzt meist einfach nur stur die gegebenen Werte in die Mitternachtsformel ein, ohne darüber nachzudenken.
Dabei ist es ganz interessant, wie man überhaupt auf die Mitternachtsformel kommt: Ihr Ursprung ist die quadratische Ergänzung.
Um das zu erkennen, musst du nur für die allgemeine Form eine quadratische Ergänzung durchführen und dann die Nullstellen berechnen (gleich null setzen):
1. Quadratische Ergänzung:
| ↓ vor den "-Termen" ausklammern. | ||
| ↓ Ergänze quadratisch mit dem Term . | ||
| ↓ Fasse zu einer binomischen Formel zusammen. | ||
| ↓ Multipliziere die Klammer aus. | ||
| ↓ Bringe die rechte Seite noch zur Vereinfachung auf einen Bruch. | ||
2. Gleich null setzen:
| ↓ | Ziehe die Wurzel. | ||
| ↓ | Löse nach auf. | ||
In der letzten Zeile steht die Mitternachtsformel.
12 Zusammenfassung
Was hast du hier gelernt?
Der Ablauf einer quadratischen Ergänzung
Eine quadratische Funktion in allgemeiner Form lässt sich über einen Kniff mit der binomischen Formel durch quadratische Ergänzung in Scheitelpunktsform umschreiben.
Dazu ist folgendes Vorgehen wichtig:
Sortieren.
bei den "-Termen" ausklammern.
Mit dem Quadrat der Hälfte des Koeffizienten des linearen Terms ergänzen (addieren und subtrahieren).
Zur 1. oder 2. binomischen Formel zusammenfassen.
Klammer ausmultiplizieren.
Summe ausrechnen.
Anwendungsmöglichkeiten der quadratischen Ergänzung
Aus der Scheitelpunktsform kann man ganz einfach die Koordinaten des Scheitelpunkts ablesen.
Quadratische Gleichungen können durch Wurzelziehen und einfaches Umformen gelöst werden.
Die quadratische Ergänzung ist die Ausgangslage für die Mitternachtsformel.
