Eine abschnittsweise definierte Funktion ist eine Funktion, die aus mindestens zwei Funktionstermen besteht, wobei die unterschiedlichen Funktionsterme unterschiedliche Definitionsmengen haben müssen (an den Stellen, an denen sie nicht übereinstimmen).
Beispiel:
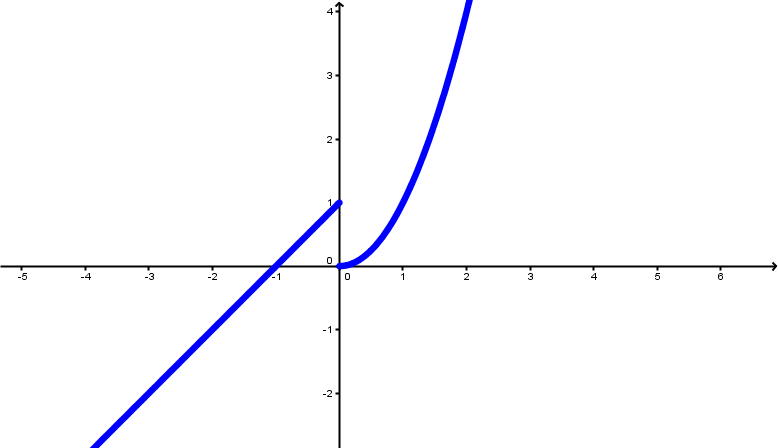
Wichtige abschnittsweise definierte Funktionen
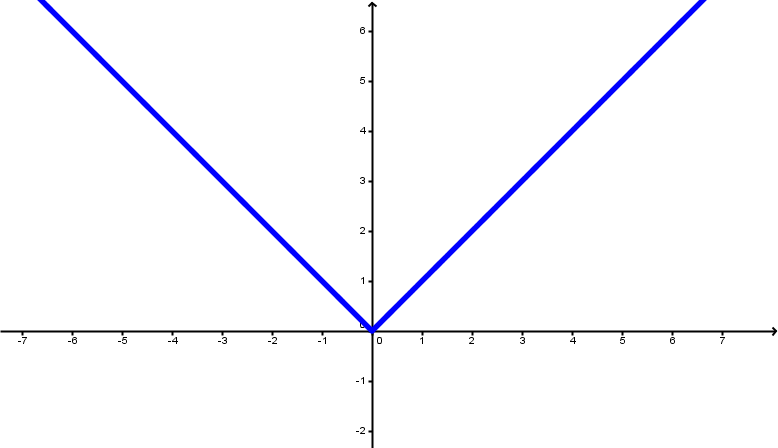
Die Betragsfunktion
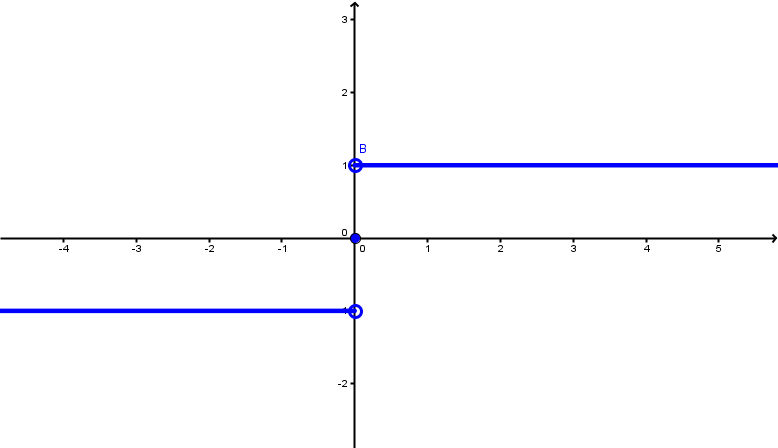
Die Signumfunktion (Vorzeichenfunktion)
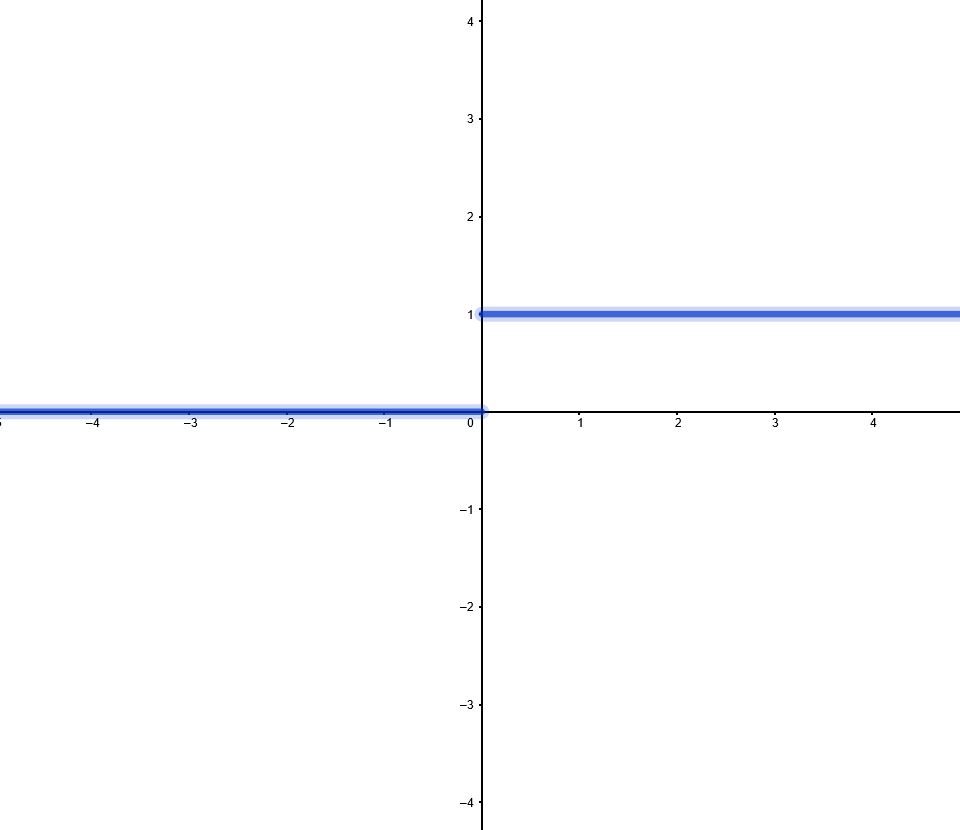
Die Heavisidefunktion
Stetigkeit von abschnittsweise definierten Funktionen
Bei abschnittsweise definierten Funktionen spielt die Untersuchung der Stetigkeit eine wesentliche Rolle.
Eine Funktion heißt stetig in , wenn . Sprich, wenn der linksseitige Grenzwert an einer Stelle, gleich dem rechtsseitigen Grenzwert und gleich dem Funktionswert ist.
Diese Stetigkeitseigenschaft zu beweisen, fällt den meisten sehr schwer. Als Faustregel kann man sagen:
ist stetig, wenn es keine Sprünge hat, also wenn du den Graphen der Funktion ohne abheben zeichnen kannst.
Auf den Intervallen, auf denen sie definiert ist, ist sie stetig und kann dort wie eine stetige Funktion behandelt werden. Das heißt, beim Skizzieren des Graphen kann sie auf diesen Abschnitten durchgehend gezeichnet werden, von Randpunkt zu Randpunkt. Nur diese sind bei der Untersuchung der Stetigkeit der springende Punkt.
Beispiele
Betragsfunktion
Die Betragsfunktion ist stetig. Beide Funktionsterme und sind stetig in . In der Schnittstelle läuft sowohl der erste Funktionsterme von rechts gegen die , als auch der zweite Funktionsterm von links gegen die . Also ist die Betragsfunktion auf ganz stetig.
Faustregel: Du kannst den Graphen ohne absetzen zeichnen. Also ist die Funktion stetig.
Signumfunktion
Die Signumfunktion ist nicht stetig in . Der erste Funktionsterm nähert sich von links an die ran, von rechts an die und die Funktion ist im Nullpunkt als definiert.
Faustregel: Da du deinen Stift im Nullpunkt mal absetzen musst, egal, wie du den Graphen zeichnest, ist die Signumfunktion nicht stetig.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Betragsfunktion
