Teil 1 Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In der Abbildung sehen Sie ausschnittsweise eine Parabel. Diese ist der Graph der Ableitungsfunktion $f'$ der Funktion $f$ mit der Definitionsmenge $D_f= \mathbb{R}$ .
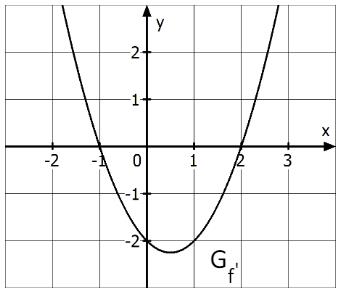
1. Leiten Sie nachvollziehbar aus dem Verlauf des Graphen der Ableitungsfunktion $f'$ die Lage und Art der lokalen Extremstellen von $f$ ab. Begründen Sie, weshalb die relativen Extrempunkte des Graphen von $f$ nicht absolut sein können.
2. Bestimmen Sie anhand des Graphen $G_{f'}$ die Lage der Wendestelle von $f$ und entscheiden Sie begründet, ob die Wendetangente des Graphen der Funktion $f$ steigt oder fällt.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
h sei eine ganzrationale Funktion dritten Grades mit der Definitionsmenge $D_h= \mathbb{R}$ . Für die zugehörige erste Ableitungsfunktion gilt die Funktionsgleichung $h'(x)=x^2+1$ . Skizzieren Sie den Graphen der Funktion $h'$ und begründen Sie damit, dass der Graph der Funktion h genau eine Nullstelle besitzt. Geben Sie außerdem einen möglichen Funktionsterm für h an.
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Im Folgenden sind zwei Gleichungen gegeben. Lösen Sie die erste und zeigen Sie die Unlösbarkeit der zweiten.
1. $2x^4-18x^2=0$
2. $e^{x+1}+e^{x-1}=0$
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Eine ganzrationale Funktion $g$ habe höchstens den Grad fünf. Die Tabelle zeigt das Krümmungsverhalten des Graphen $G_g$ .
Geben Sie die Wendestellen der Funktion $g$ an und argumentieren Sie, welchen Grad $g$ nur haben kann.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?