Analysis, Teil B, Aufgabengruppe 1

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f: x \mapsto \; e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}$ . Der Graph von $f$ wird mit $G_f$ bezeichnet.

Bestimmen Sie die Koordinaten des Schnittpunkts von $G_f$ mit der $y$ -Achse und begründen Sie, dass $G_f$ oberhalb der $x$ -Achse verläuft. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt mit der y-Achse
Schnittpunkt mit der $y$ -Achse
Bestimme den Schnittpunkt mit der y-Achse, indem du $x=0$ in die Funktion einsetzt.
$f(0)=e^{\frac{1}{2}\cdot 0}+e^{-\frac{1}{2}\cdot 0}$
Überlege, welche Auswirkungen der Exponent $0$ hat.
$f(0)=1+1=2$
Der $y$ -Achsenabschnitt ist also $2$ .
Achte aber genau auf die Fragestellung! Gesucht ist der Schnittpunkt, diesen musst du noch mit seinen Koordinaten angeben.
$SP=(0|2)$
Begründung des Verlaufes oberhalb der $x$ -Achse
Die Exponentialfunktion verläuft immer oberhalb der $x$ -Achse. Dies gilt auch wenn man eine negative Zahl für $x$ einsetzt. So verlaufen auch $e^{\frac{1}{2}x}$ und $e^{-\frac{1}{2}x}$ oberhalb der $x%$ -Achse. Dies gilt folglich auch für die Summe $e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Tipp: Insgesamt hast du für den Prüfungsteil B 180 Minuten Zeit. Da der Analysis Teil die Hälfte der Punkte gibt, kannst du auch ungefähr die Hälfte der Zeit für diesen Teil einplanen. Aufgabe 1 umfasst ungefähr $\frac{2}{3}$ der Punkte, also hast du ungefähr 60 Minuten Zeit für 26 Punkte, d.h. ungefähr 2 Minuten für einen Punkt. Mach dir keine Sorgen, lies vor allem genau und beachte genau, welche Informationen du benötigst und welche nicht.
Probiere es doch erst einmal selbst. Die Lösungen findest du dann Schritt für Schritt auf den nächsten Seiten.
Ermitteln Sie das Symmetrieverhalten von $G_f$ sowie das Verhalten von $f$ für $x \to -\infty$ und für $x \to \infty$ . (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrieverhalten
Erinnere dich an das Vorgehen zur Bestimmung von Symmetrieverhalten. Setze für alle $x$ nun $\color{red}{-x}$ ein und überprüfe, ob eine der folgenden Gleichheiten gilt.
Achsensymmetrie (zur $y$ -Achse): $f({\color{red}-x})=f(x)$
Punktsymmetrie (zum Ursprung): $f({\color{red}-x})=-f(x)$
$f({\color{red}-x})=e^{\frac{1}{2}\cdot ({\color{red}-x})}+e^{-\frac{1}{2}\cdot({\color{red}-x})}$
$f({\color{red}-x})=e^{-\frac{1}{2}x}+e^{\frac{1}{2}x}$
Du musst nur noch die Summanden vertauschen…
$f({\color{red}-x})=e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}$
… und schon bist du wieder bei der Ausgangsfunktion. Daraus folgt:
$f({\color{red}-x})=f(x)$
Verhalten minus unendlich
Beachte, dass du Unendlich nicht wirklich in die Funktion einsetzen darfst, da dies keine offizielle Schreibweise ist. Benutze einfach Anführungszeichen, damit bist du auf der sicheren Seite.
Was macht das minus Unendlich im Exponenten? Achte auf die Vorzeichen.
Verhalten plus unendlich
Was macht das Unendlich im Exponenten? Achte auf die Vorzeichen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Zeigen Sie, dass für die zweite Ableitung $f''$ von $f$ die Beziehung $f''(x)=\frac{1}{4}\cdot f(x)$ für $x\in \mathbb{R}$ gilt. Weisen Sie nach, dass $G_f$ linksgekrümmt ist. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung

Zweite Ableitung von $f$

Um die zweite Ableitung zu bestimmen, benötigst du zunächst die erste Ableitung. Beachte dazu die Ableitungsregeln.

$\displaystyle f´\left(x\right)$	$=$	$\displaystyle e^{\frac{1}{2}x}\cdot\frac{1}{2}+e^{-\frac{1}{2}x}\cdot(-\frac{1}{2})$
	↓	Fasse so weit wie möglich zusammen.
$\displaystyle f´\left(x\right)$	$=$	$\displaystyle \frac{1}{2}\cdot e^{\frac{1}{2}x}-\frac{1}{2}\cdot e^{-\frac{1}{2}x}$
	↓	Kannst du noch etwas ausklammern?
$\displaystyle f´\left(x\right)$	$=$	$\displaystyle \frac{1}{2}\cdot\left(e^{\frac{1}{2}x}-e^{-\frac{1}{2}x}\right)$
	↓	Damit bist du beim Kontrollergebnis.

Leite die Ableitung noch einmal ab. Beachte wieder die Ableitungsregeln.

$\displaystyle f´´\left(x\right)$	$=$	$\displaystyle \frac{1}{2}\cdot\left(e^{\frac{1}{2}x}\cdot\frac{1}{2}-e^{-\frac{1}{2}x}\cdot(-\frac{1}{2})\right)$
	↓	Kannst du noch etwas ausklammern? Achte auf die Vorzeichen.
$\displaystyle f´´\left(x\right)$	$=$	$\displaystyle \frac{1}{2}\cdot\frac{1}{2}\cdot\left(e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}\right)$
$\displaystyle f´´\left(x\right)$	$=$	$\displaystyle \frac{1}{4}\cdot\left(e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}\right)$
	↓	In der Klammer steht die Funktionsgleichung von $f(x)$ . Daraus folgt:
$\displaystyle f´´\left(x\right)$	$=$	$\displaystyle \frac{1}{4}\cdot f(x)$
	↓	Linkskrümmung nachweisen. Damit eine Linkskrümmung vorliegt, muss die zweite Ableitung immer positiv sein.
$\displaystyle f´´\left(x\right)$	$=$	$\displaystyle \frac{1}{4}\cdot f(x)$
	↓	Du hast schon gezeigt, dass die Funktion $f(x)$ immer oberhalb der $x$ -Achse verläuft, also gilt immer:
$\displaystyle f\left(x\right)$	$>$	$\displaystyle 0$

Daraus folgt:

$f''(x)=\frac{1}{4}\cdot f(x)>0$

Und damit gilt dann auch:

$\Rightarrow$ $f$ ist linksgekrümmt

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Bestimmen Sie Lage und Art des Extrempunkts von $G_f$ . (3 BE)

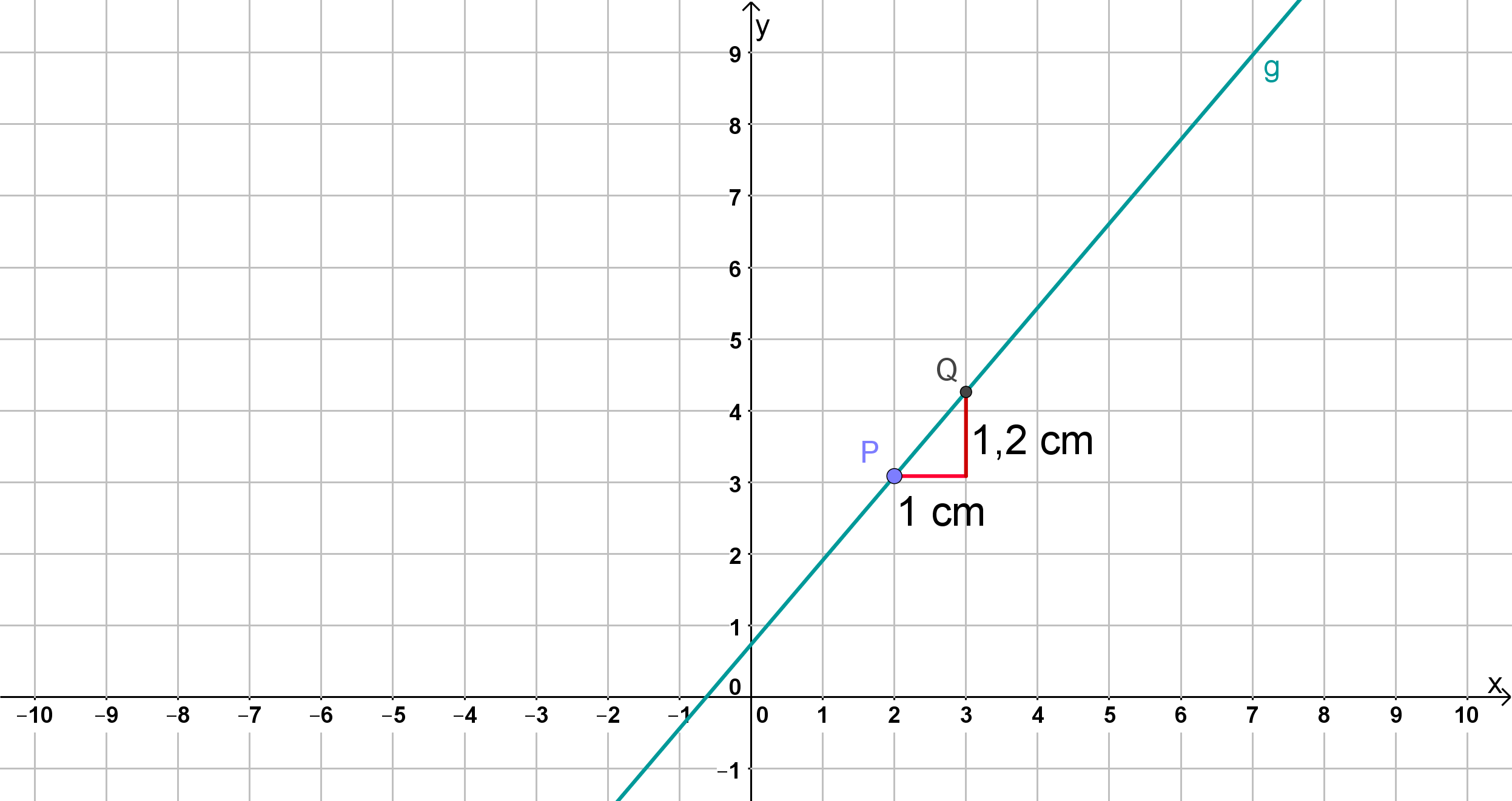
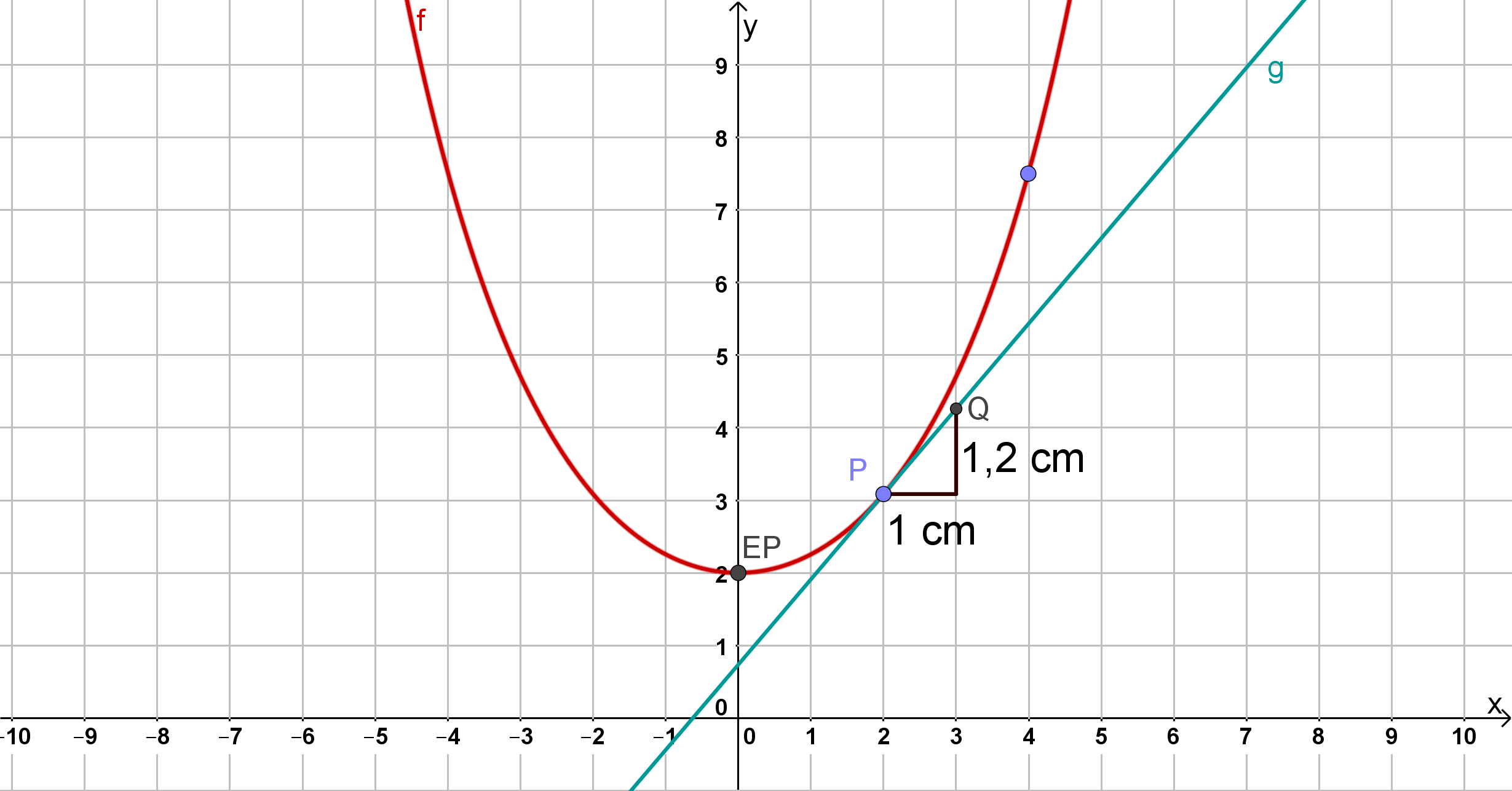
Berechnen Sie die Steigung der Tangente $g$ an $G_f$ im Punkt $P(2|f(2))$ auf eine Dezimale genau. Zeichnen Sie den Punkt $P$ und die Gerade $g$ in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: $-4\leq x\leq4$ , $-1 \leq y \leq 9$ ). (3 BE)

Berechnen der Tangentensteigung
Die Steigung der Tangente ist per Definition gleich zur Ableitung in einem Punkt. Setze also $x=2$ in die erste Ableitung ein.
$\def\arraystretch{1.25} \begin{array}{rcl}&f'(2)&=&\frac{1}{2}\cdot\left(e^{\frac{1}{2}\cdot2}-e^{-\frac{1}{2}\cdot 2}\right)\\&&=& \frac{1}{2}\cdot\left(e^1-e^{-1}\right)\\&&\approx& 1{,}2\end{array}$
Die Steigung ist also $1{,}2$
Zeichnen des Punktes und der Tangente
$\def\arraystretch{1.25} \begin{array}{rcl} f(2)&=& e^{\frac{1}{2}\cdot 2}+e^{-\frac{1}{2}\cdot 2}\\&=& e^1 + e^{-1}\\&\approx & 3{,}1\end{array}$
Die Koordinaten des Punktes sind also $P(2∣3{,}1)$ .
Du zeichnest den Punkt Punkt $P$ in ein Koordinatensystem und bestimmst mit Hilfe eines Steigungsdreiecks einen weiteren Punkt $Q$ . Diese beiden Punkte verbindest du zu der Geraden $g$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Berechnen Sie $f(4)$ , im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse $G_f$ im Bereich $-4 \leq x \leq 4$ in das Koordinatensystem aus Aufgabe 1e ein. (4 BE)

Zeigen Sie durch Rechnung, dass für $x \in \mathbb{R}$ die Beziehung $\quad \frac{1}{4}\cdot [f(x)]^2-[f'(x)]^2=1$ gilt. (3 BE)

Die als Kurvenlänge $L_{a;b}$ bezeichnete Länge des Funktionsgraphen von $f$ zwischen den Punkten $(a|f(a))$ und $(b|f(b))$ mit $a<b$ lässt sich mithilfe der Formel $L_{a;b}=\int_a^b\sqrt{1+[f'(x)]^2}\text{d}x$ berechnen.

Rechnung: Setze ein und vereinfache.
	↓
$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}&& \frac{1}{4}\cdot [f(x)]^2-[f'(x)]^2\end{array}$	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot \left[e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}\right]^2-\left[\frac{1}{2}\cdot\left(e^{\frac{1}{2}x}-e^{-\frac{1}{2}x}\right)\right]^2\end{array}$
	↓	Beachte, dass du jetzt die binomischen Formeln anwenden musst!
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\\\frac{1}{4}\cdot\left[(e^{\frac{1}{2}x})^2+2\cdot e^{\frac{1}{2}x} \cdot e^{-\frac{1}{2}x} + (e^{-\frac{1}{2}x} )^2\right]-\left[(\frac{1}{2})^2\cdot (e^{\frac{1}{2}x}-e^{-\frac{1}{2}x})^2\right]\end{array}$
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[(e^{\frac{1}{2}x})^2+2\cdot e^{\frac{1}{2}x}\cdot e^{-\frac{1}{2}x}+(e^{-\frac{1}{2}x} )^2\right]-\left[\frac{1}{4}\cdot\left((e^{\frac{1}{2}x})^2-2\cdot e^{\frac{1}{2}x}\cdot e^{-\frac{1}{2}x}+(e^{-\frac{1}{2}x} )^2\right)\right]\end{array}$
	↓	Überlege jetzt, wie sich die Exponenten zusammen addieren bzw. multiplizieren. Die Potenzgesetze helfen dir dabei.
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[(e^{\frac{1}{2}x})^2+2\cdot e^{\frac{1}{2}x} \cdot e^{-\frac{1}{2}x} + (e^{-\frac{1}{2}x} )^2\right]-\left[\frac{1}{4}\cdot \left((e^{\frac{1}{2}x})^2-2\cdot e^{\frac{1}{2}x} \cdot e^{-\frac{1}{2}x} + (e^{-\frac{1}{2}x} )^2\right)\right]\end{array}$
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[e^{x}+2\cdot e^{0}+e^{-x}\right]-\left[\frac{1}{4}\cdot \left(e^{x}-2\cdot e^{0}+e^{-x} \right)\right]\end{array}$
	↓	Spätestens jetzt kannst du die $\frac{1}{4}$ aus der zweiten Klammer herausziehen und ganz ausklammern.
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[e^{x}+2\cdot e^{0} + e^{-x} -\left(e^{x}-2\cdot e^{0} + e^{-x} \right)\right]\end{array}$
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[e^{x}+2\cdot e^{0}+e^{-x}-e^{x}+2\cdot e^{0}-e^{-x} \right]\end{array}$
	↓	Spätestens jetzt kannst du wiederum die $e^0$ durch $1$ ersetzen. Vereinfache außerdem so weit wie möglich.
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[e^{x}+2\cdot 1 + e^{-x} -e^{x}+2\cdot 1 - e^{-x} \right]\end{array}$
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot\left[2+2\right]\end{array}$
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}\frac{1}{4}\cdot 4\end{array}$
	$=$	$\def\arraystretch{1.25} \displaystyle \begin{array}{ll}1\end{array}$

Geschafft! :) Damit ist die Gleichung gezeigt.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Bestimmen Sie mithilfe der Beziehung aus Aufgabe $1g$ die Kurvenlänge $L_{0;b}$ des Graphen von $f$ zwischen den Punkten $(0|f(0))$ und $(b|f(b))$ mit $b>0$ . (4 BE)

Umformung der Beziehung aus $1g)$

$\begin {array}{rrllll}\frac{1}{4}\cdot [f(x)]^2&-&[f'(x)]^2&=&1\quad &|+[f'(x)]^2\\\frac{1}{4}\cdot [f(x)]^2&&&=&1+[f'(x)]^2\end{array}$

Jetzt kannst du anstatt der rechten Seite, die unter der Wurzel im Integral steht, auch die linke Seite benutzen, da diese äquivalent sind.

Bestimmung des Integrals

Erinnere dich, auf was du bei der Berechnung eines Integrals alles achten musst. In dem Text über der Aufgabenstellung steht $L_{a;b}=\int_a^b\sqrt{1+[f'(x)]^2}\text{d}x$ . In der Aufgabenstellung heißt es aber, du sollst $L_{0;b}$ ausrechnen. Die Grenzen des Integrals sind also nicht die gleichen.

$\displaystyle L_{a;b}$	$=$	$\displaystyle \int_a^b\sqrt{1+[f'(x)]^2}\text{d}x$
$\displaystyle L_{0;b}$	$=$	$\displaystyle \int_0^b\sqrt{1+[f'(x)]^2}\text{d}x$
	↓	Verändere jetzt die Wurzel mit der Beziehung aus $1g$ die du gerade ausgerechnet hast.
$\displaystyle L_{0;b}$	$=$	$\displaystyle \int_0^b\sqrt{\frac{1}{4}\cdot[f(x)]^2}\text{d}x$
	↓	Schau genau hin! Die Wurzel und das Quadrat kürzen sich und $\frac{1}{4}$ kannst du ebenfalls aus der Wurzel ziehen.
$\displaystyle L_{0;b}$	$=$	$\displaystyle \int_0^b\frac{1}{2}\cdot[f(x)]\text{d}x$
$\displaystyle L_{0;b}$	$=$	$\displaystyle \int_0^b\frac{1}{2}\cdot(e^{\frac{1}{2}x}+e^{-\frac{1}{2}x})\text{d}x$
	↓	Das $\frac{1}{2}$ kannst du als Vorfaktor aus dem Integral heraus ziehen.
$\displaystyle L_{0;b}$	$=$	$\displaystyle \frac{1}{2}\cdot\int_0^b(e^{\frac{1}{2}x}+e^{-\frac{1}{2}x})\text{d}x$
	↓	Berechne das Integral. Erinnere dich, wie du die Exponentialfunktion aufleitest und wie du beim Integrieren "nachdifferenzierst".
$\displaystyle L_{0;b}$	$=$	$\displaystyle \frac{1}{2}\cdot\left[(2\cdot e^{\frac{1}{2}x}-2\cdot e^{-\frac{1}{2}x})\right]_0^b$
$\displaystyle L_{0;b}$	$=$	$\displaystyle \frac{1}{2}\cdot\left[(2\cdot e^{\frac{1}{2}\cdot b}-2\cdot e^{-\frac{1}{2}\cdot b})-(2\cdot e^{\frac{1}{2}\cdot0}-2\cdot e^{-\frac{1}{2}\cdot0})\right]$
	↓	Beachte: $e^0=1$
$\displaystyle L_{0;b}$	$=$	$\displaystyle \frac{1}{2}\cdot\left[2\cdot e^{\frac{1}{2}\cdot b}-2\cdot e^{-\frac{1}{2}\cdot b}\right]$
$\displaystyle L_{0;b}$	$=$	$\displaystyle \frac{1}{2}\cdot\left[2\cdot(e^{\frac{1}{2}\cdot b}-e^{-\frac{1}{2}\cdot b})\right]$
$\displaystyle L_{0;b}$	$=$	$\displaystyle \frac{1}{2}\cdot2\cdot(e^{\frac{1}{2}\cdot b}-e^{-\frac{1}{2}\cdot b})$
$\displaystyle L_{0;b}$	$=$	$\displaystyle e^{\frac{1}{2}\cdot b}-e^{-\frac{1}{2}\cdot b}$

Und schon bist du beim richtigen Ergebnis. Super gemacht! :)

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$\displaystyle e^{\frac{1}{2}x}$	$=$	$\displaystyle e^{-\frac{1}{2}x}$	$\displaystyle \ln\left(\right)$
$\displaystyle \frac{1}{2}x$	$=$	$\displaystyle -\frac{1}{2}x$	$\displaystyle \cdot2$
$\displaystyle x$	$=$	$\displaystyle -x$

$\displaystyle f\left(4\right)$	$=$	$\displaystyle e^{\frac{1}{2}\cdot4}+e^{-\frac{1}{2}\cdot4}$
	$=$	$\displaystyle e^2+e^{-2}$
	$≈$	$\displaystyle 7{,}52$

Schnittpunkt mit der $y$ -Achse

Begründung des Verlaufes oberhalb der $x$ -Achse

Hast du eine Frage oder Feedback?

Verhalten minus unendlich

Verhalten plus unendlich

Hast du eine Frage oder Feedback?

Zweite Ableitung von $f$

Linkskrümmung nachweisen. Damit eine Linkskrümmung vorliegt, muss die zweite Ableitung immer positiv sein.

Hast du eine Frage oder Feedback?

Lage des Extrempunkts

Art des Extrempunkts

Hast du eine Frage oder Feedback?

Berechnen der Tangentensteigung

Zeichnen des Punktes und der Tangente

$\def\arraystretch{1.25} \begin{array}{rcl} f(2)&=& e^{\frac{1}{2}\cdot 2}+e^{-\frac{1}{2}\cdot 2}\\&=& e^1 + e^{-1}\\&\approx & 3{,}1\end{array}$

Hast du eine Frage oder Feedback?

Berechnung von $f(4)$

Graph von $G_f$

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Umformung der Beziehung aus $1g)$

$\begin {array}{rrllll}\frac{1}{4}\cdot [f(x)]^2&-&[f'(x)]^2&=&1\quad &|+[f'(x)]^2\\\frac{1}{4}\cdot [f(x)]^2&&&=&1+[f'(x)]^2\end{array}$

Bestimmung des Integrals

Hast du eine Frage oder Feedback?

Schnittpunkt mit der yyy-Achse

Begründung des Verlaufes oberhalb der xxx-Achse

Hast du eine Frage oder Feedback?

Verhalten minus unendlich

Verhalten plus unendlich

Hast du eine Frage oder Feedback?

Zweite Ableitung von fff

Linkskrümmung nachweisen. Damit eine Linkskrümmung vorliegt, muss die zweite Ableitung immer positiv sein.

Hast du eine Frage oder Feedback?

Lage des Extrempunkts

Art des Extrempunkts

Hast du eine Frage oder Feedback?

Berechnen der Tangentensteigung

Zeichnen des Punktes und der Tangente

f(2)=e12⋅2+e−12⋅2=e1+e−1≈3,1\def\arraystretch{1.25} \begin{array}{rcl} f(2)&=& e^{\frac{1}{2}\cdot 2}+e^{-\frac{1}{2}\cdot 2}\\&=& e^1 + e^{-1}\\&\approx & 3{,}1\end{array}f(2)​==≈​e21​⋅2+e−21​⋅2e1+e−13,1​

Hast du eine Frage oder Feedback?

Berechnung von f(4)f(4)f(4)

Graph von GfG_fGf​

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Umformung der Beziehung aus 1g)1g)1g)

14⋅[f(x)]2−[f′(x)]2=1∣+[f′(x)]214⋅[f(x)]2=1+[f′(x)]2\begin {array}{rrllll}\frac{1}{4}\cdot [f(x)]^2&-&[f'(x)]^2&=&1\quad &|+[f'(x)]^2\\\frac{1}{4}\cdot [f(x)]^2&&&=&1+[f'(x)]^2\end{array}41​⋅[f(x)]241​⋅[f(x)]2​−​[f′(x)]2​==​11+[f′(x)]2​∣+[f′(x)]2

Bestimmung des Integrals

Hast du eine Frage oder Feedback?

Schnittpunkt mit der $y$ -Achse

Begründung des Verlaufes oberhalb der $x$ -Achse

Zweite Ableitung von $f$

$\def\arraystretch{1.25} \begin{array}{rcl} f(2)&=& e^{\frac{1}{2}\cdot 2}+e^{-\frac{1}{2}\cdot 2}\\&=& e^1 + e^{-1}\\&\approx & 3{,}1\end{array}$

Berechnung von $f(4)$

Graph von $G_f$

Umformung der Beziehung aus $1g)$

$\begin {array}{rrllll}\frac{1}{4}\cdot [f(x)]^2&-&[f'(x)]^2&=&1\quad &|+[f'(x)]^2\\\frac{1}{4}\cdot [f(x)]^2&&&=&1+[f'(x)]^2\end{array}$