Spurpunkte einer Ebene

Anzahl der Spurpunkte

• $1$ Spurpunkt$\;\Rightarrow\;$Ebene ist echt parallel zu einer Koordinatenebene

• $2$ Spurpunkte$\;\Rightarrow\;$Ebene ist echt parallel zu einer Koordinatenachse und nicht parallel zu einer Koordinatenebene

• $3$ Spurpunkte$\;\Rightarrow\;$Ebene ist weder zu einer Koordinatenebene noch zu einer Koordinatenachse parallel

Sonderfälle:

• Ebene geht durch den Koordinatenursprung und ist nicht parallel zu einer Koordinatenebene$\;\Rightarrow\;$ $1$ Spurpunkt im Koordinatenursprung

• Ebene enthält eine Koordinatenachse $\Rightarrow\;$ unendlich viele Spurpunkte

• Ebene liegt in einer Koordinatenebene $\Rightarrow\;$unendlich viele Spurpunkte

Wie werden die Spurpunkte berechnet?

Die Ebene $E$ kann in verschiedenen Formen vorliegen.

Man geht davon aus, dass sie in Koordinatenform vorliegt.

Anmerkung: Liegt die Ebene in Parameterform vor, ist es sinnvoll, diese Ebene in die Koordinatenform umzuwandeln. Möchte man die Parameterform nicht umwandeln, befindet sich die "Vorgehensweise für eine Ebene in Parameterform" zum Ausklappen im Artikel weiter unten.

Beispiel für die Berechnung der Spurpunkte

Gegeben ist die Ebene $E:\;2x_1-4x_2+3x_3=6$ in Koordinatenform.

Berechne ihre möglichen Spurpunkte (Achsenschnittpunkte).

Berechnung des Spurpunktes $S_{1}​$

Für den Spurpunkt $S_{1}$ (Schnittpunkt mit der $x_1$-Achse) setzt man $x_2$ und $x_3$ gleich null und berechnet $x_1$:

Der Spurpunkt $S_{1}$ hat die Koordinaten $S_{1}(3|0|0)$.

Graphische Darstellung

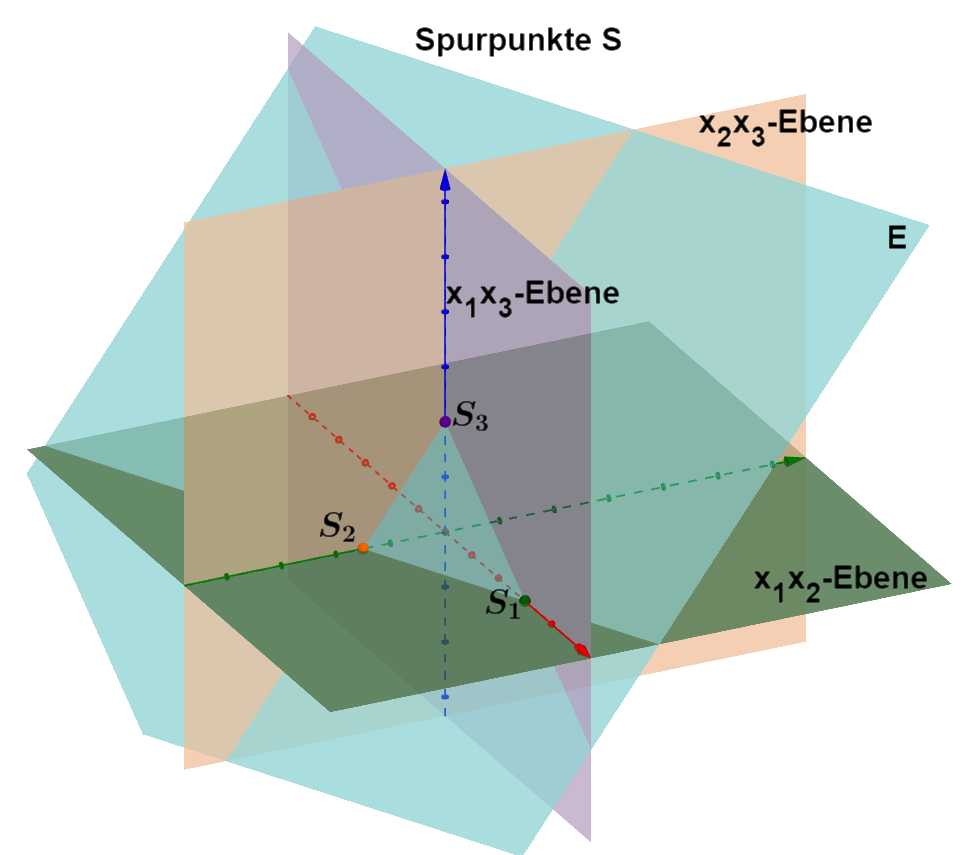
Allgemeine Vorgehensweise für die Berechnung der Spurpunkte

Gegeben ist die Ebene $E:\;ax_1+bx_2+cx_3=d$ in Koordinatenform.

Bestimme die möglichen Spurpunkte von $E$.

Berechnung des Spurpunktes $S_{1}​$

Für den Spurpunkt $S_{1}$ (Schnittpunkt mit der $x_1$-Achse) setzt man $x_2$ und $x_3$ gleich null und berechnet $x_1$:

Eine Lösung ergibt sich nur für $a\neq 0$, andernfalls ist die Ebene $E$ parallel zur $x_1$-Achse oder die Ebene $E$ enthält die $x_1$-Achse.

Die Ebene $E$ schneidet die $x_1$-Achse im Punkt $S_{1}\left(\frac{d}{a}\big\vert 0\big\vert 0\right)$

Für die anderen beiden Spurpunkte $S_{2}$ und $S_{3}$ geht man analog vor.