Aufgabengruppe I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
Lösen Sie die folgenden Aufgaben:
Ermitteln Sie rechnerisch die Funktionsgleichung der nach oben geöffneten Normalparabel mit dem Scheitelpunkt in der Normalform.
Die nach unten geöffnete Normalparabel geht durch die Punkte und . Ermitteln Sie rechnerisch die Funktionsgleichung von in der Scheitelpunktform und geben Sie den Scheitelpunkt an.
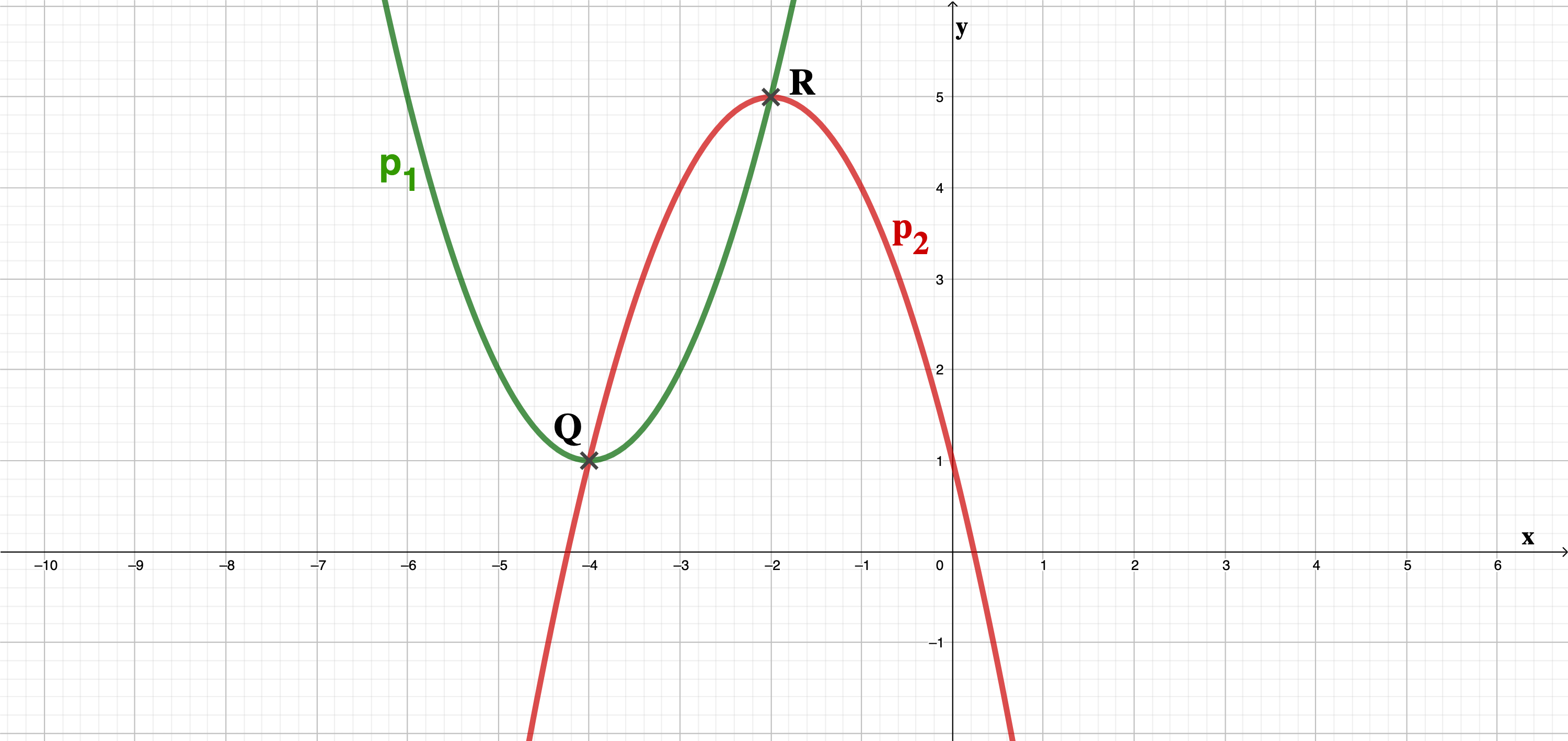
Bestimmen Sie zeichnerisch die Koordinaten der Schnittpunkte und der beiden Normalparabeln und in einem Koordinatensystem mit der Längeneinheit 1 cm. Geben Sie und an.
Die Normalparabeln sowie schneiden sich in den Punkten und . Berechnen Sie die Koordinaten von und und geben Sie beide Punkte an.
- 2
Der Neupreis eines Autos beträgt 37450 €.
Berechnen Sie, in wie vielen Jahren sich der Wert dieses Autos auf 25000 € verringert, wenn man von einem jährlich gleichbleibenden prozentualen Wertverlust von 12,7 % ausgeht.
JahreDer Neuwagen soll nach acht Jahren als Gebrauchtwagen für 9000 € verkauft werden. Bestimmen Sie für diesen Fall den Wertverlust pro Jahr in Prozent, unter der Annahme, dass dieser über die Jahre hinweg gleich bleibt.
%Tatsächlich ist der Wertverlust aber nicht gleichbleibend. Im ersten Jahr beträgt er 25 %, im zweiten Jahr 18 % und in den darauffolgenden vier Jahren jeweils 9%. Ermitteln Sie den Wert des Autos nach diesen 6 Jahren.
€
- 3
Die folgende Abbildung zeigt eine Figur, bei der gilt: ; ;
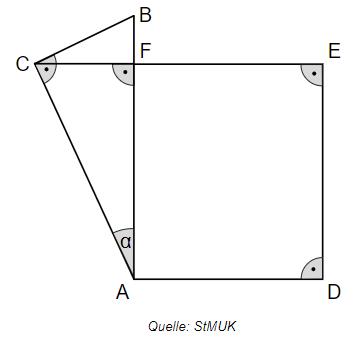
Berechnen Sie den Flächeninhalt des Dreiecks ABC.
cm² - 4
Vereinfachen Sie den unten stehenden Term soweit wie möglich. Es gilt:
- 5
Lösen Sie die folgenden Aufgaben.
Die Gerade verläuft durch den Punkt und hat die Steigung . Bestimmen Sie rechnerisch die Funktionsgleichung von .
Berechnen Sie die x-Koordinate der Nullstelle der Gerade
=xDer Punkt liegt auf . Berechnen Sie die fehlende y-Koordinate.
=yDie Gerade durch den Punkt steht senkrecht auf der Geraden
. Ermitteln Sie rechnerisch die Funktionsgleichung von .
Die Gerade mit der Funktionsgleichung schneidet die Gerade im Punkt . Bestimmen Sie rechnerisch die Koordinaten des Schnittpunkts .
Ermitteln Sie rechnerisch die Funktionsgleichung der Geraden , auf der die Punkte und liegen.
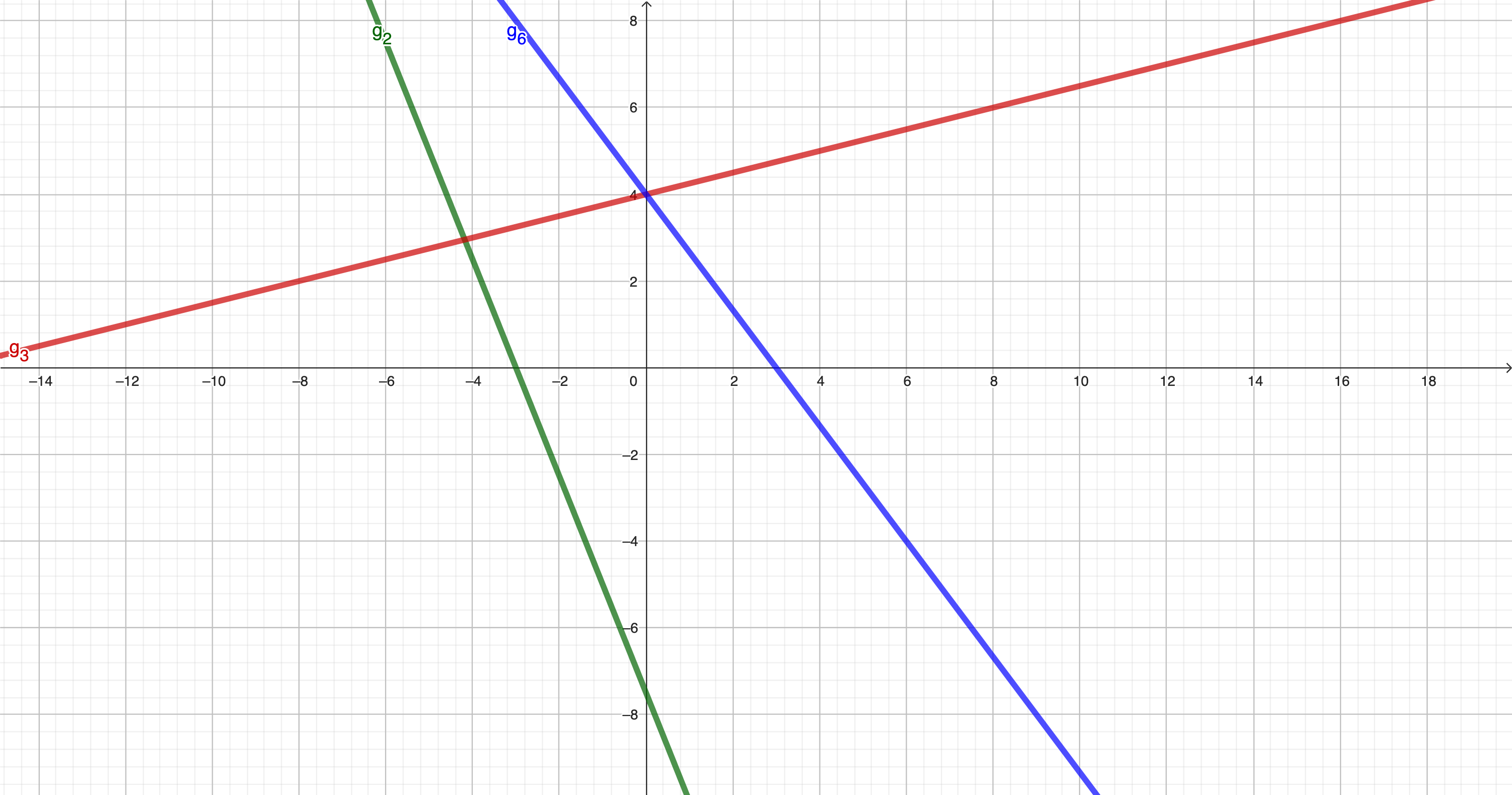
Zeichnen Sie die Geraden , und in ein Koordinatensystem mit der Längeneinheit 1 cm.
- 6
Gegeben ist folgende Gleichung:
Geben Sie die Definitionsmenge an, lösen Sie die Gleichung nach auf und bestimmen Sie die Lösungsmenge.
- 7
In einer Firma werden vier gleich große Pralinenkugeln, die vollständig mit Marzipan gefüllt sind, mit einem Durchmesser von jeweils 3 cm übereinander in eine Schachtel verpackt.
Die zylinderförmige Verpackung hat eine Höhe von und einen Innendurchmesser von . Berechnen Sie den prozentualen Anteil der Luft in der Schachtel am Innenvolumen der Schachtel nach dem Verpacken der vier Pralinen.
Jede Pralinenkugel soll mit einer dünnen Blattgoldschicht überzogen werden. Berechnen Sie, wie viele Blattgold für eine Pralinenkugel mindestens benötigt werden.
Bestimmen Sie die Masse einer massiven Kugel aus Gold mit einem Volumen von . Dabei wiegt ein Gold .
- 8
Ein Gemälde mit der Breite soll vollständig ausgeleuchtet werden (siehe Skizze, die eine Ansicht von oben darstellt). Wenn sich der Scheinwerfer entfernt befindet (A), bleiben insgesamt der Bildbreite schlecht beleuchtet. Um die ganze Breite gut auszuleuchten, wird die Lichtquelle um verschoben (A‘). Ermitteln Sie rechnerisch die Breite und die Größe des Winkels α.
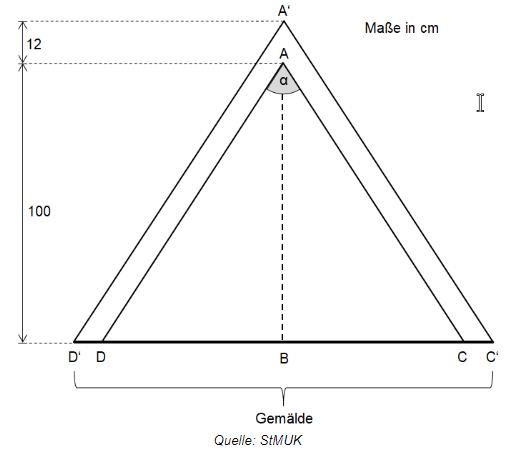
Hinweis: Skizze nicht maßstabsgetreu
- 9
Bei den folgenden Umformungen werden die binomischen Formeln angewendet. Ersetzen Sie die Platzhalter jeweils durch den entsprechenden Term und ermitteln Sie die mathematisch richtige Gleichung.
I.
II.
- 10
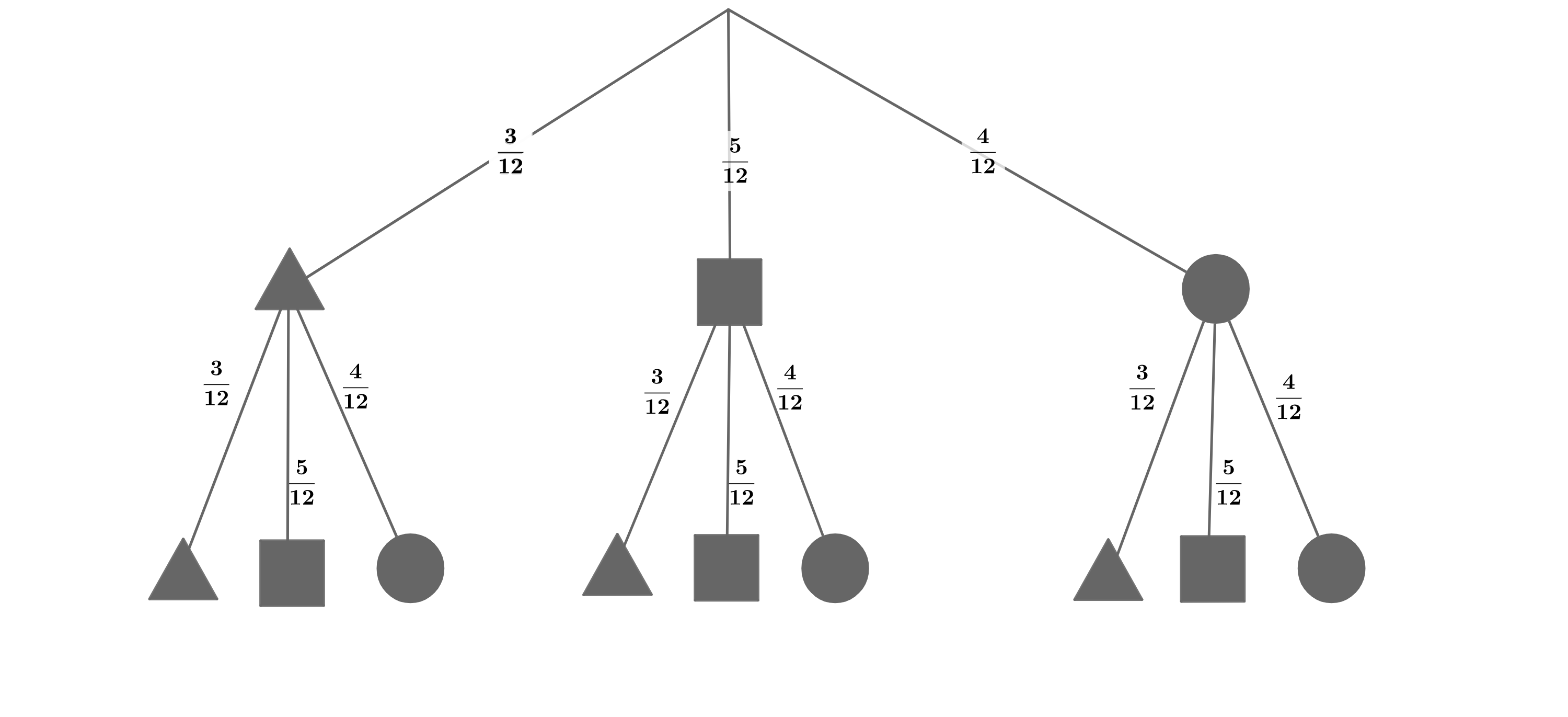
Ein Glücksrad ist in gleich große Sektoren unterteilt. Auf jedem Feld befindet sich eines von drei Symbolen (siehe Skizze).
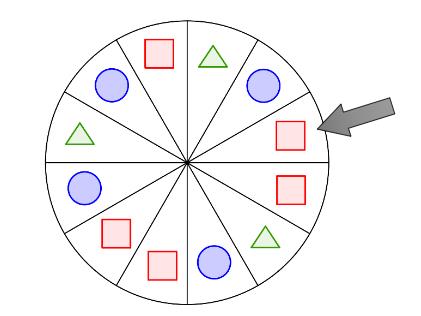
Das Glücksrad wird zweimal nacheinander gedreht. Zeichnen Sie ein Baumdiagramm mit den möglichen Ergebnissen und beschriften Sie die Äste mit den entsprechenden Wahrscheinlichkeiten.
Das Glücksrad wird dreimal nacheinander gedreht. Berechnen Sie, mit welcher Wahrscheinlichkeit der Pfeil zuerst auf ein Dreieck, dann auf ein Viereck und danach auf einen Kreis zeigt, und geben Sie diese in Prozent an.
%Das Glücksrad wird viermal nacheinander gedreht. Berechnen Sie die Wahrscheinlichkeit in Prozent, dass nicht viermal hintereinander ein Kreis angezeigt wird.
%
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?