Aufgaben zur Betragsfunktion

Wie gut kennst du dich mit der Betragsfunktion aus? Vertiefe dein Wissen mit diesen gemischten Übungsaufgaben!

$f (x) = 3 \cdot (x^{2} - 4) \cdot (| x | + 1)$

Untersuche $f (x)$ auf Stetigkeit und Differenzierbarkeit.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktion betragsfrei machen
$f (x) = 3 \cdot (x^{2} - 4) (| x | + 1)$
Um den Betrag zu eliminieren muss eine Fallunterscheidung ( für x $\geq$ 0 und x < 0 durchgeführt werden.
Fall x $\geq$ 0
Da x $\geq$ 0 ist, kann der Betrag weggelassen werden.
$f (x)$ $=$ $3 \cdot (x^{2} - 4) (x + 1)$
↓
Die Klammern ausmultiplizieren.
$=$ $3 x^{3} + 3 x^{2} - 12 x - 12$
Fall x<0
Da x < 0 ist wird -x für $| x |$ eingesetzt.
$f (x)$ $=$ $3 \cdot (x^{2} - 4) (- x + 1)$
↓
Die Klammern ausmultiplizieren.
$=$ $- 3 x^{3} + 3 x^{2} + 12 x - 12$
Stetigkeit
Für x>0 und x<0 ist f(x) stetig.
Untersucht werden muss nur der Fall x=0.
f(0) berechnen mit Fall x $\geq$ 0
$f (x)$ $=$ $3 x^{3} + 3 x^{2} - 12 x - 12$
$f (0)$ $=$ $- 12$
Annäherung an 0 von links
$\lim_{x \to 0^{-}} f (x)$ $=$
↓
Es muss der Term ausgewählt werden, der für x<0 gilt.
$=$ $\lim_{x \to 0^{-}} (- 3 x^{3} + 3 x^{2} + 12 x - 12)$
↓
0 einsetzen.
$=$ $- 12$
Annäherung an 0 von rechts
$\lim_{x \to 0^{+}} f (x)$ $=$
↓
Es muss der Term ausgewählt werden, der für x>0 gilt.
$=$ $\lim_{x \to 0^{+}} (3 x^{3} + 3 x^{2} - 12 x - 12)$
↓
0 einsetzen.
$=$ $- 12$
$\lim_{x \to 0^{-}} f (x) = \lim_{x \to 0^{+}} f (x) = f (0) \Rightarrow$ f ist bei 0 stetig .
Differenzierbarkeit
$f (x) = 3 \cdot (x^{2} - 4) (| x | + 1)$
Es muss eine Fallunterscheidung für x durchgeführt werden.
Fall: x $\geq$ 0
Siehe Teilaufgabe a.
$f (x)$ $=$ $3 x^{3} + 3 x^{2} - 12 x - 12$
↓
Erste Ableitung bilden.
$f ‘ (x)$ $=$ $9 x^{2} + 6 x - 12$
Fall: x<0
Siehe Teilaufgabe a.
$f (x)$ $=$ $- 3 x^{3} + 3 x^{2} + 12 x - 12$
↓
Erste Ableitung bilden.
$f ´ (x)$ $=$ $- 9 x^{2} + 6 x + 12$
Fall x=0
Das Verhalten der Steigung an der Stelle x=0 muss wegen des Betrages gesondert untersucht werden. Hierzu muss man für diesen Punkt die Ableitung durch Annäherung von links und rechts betrachten.
Bei Annäherung von links, muss $f ‘ (x) = - 9 x^{2} + 6 x + 12$ betrachtet werden, da x<0.
$\lim_{x \to 0^{-}} (- 9 x^{2} + 6 x + 12)$ $=$ $12$
↓
Bei Annäherung von rechts, muss $f ‘ (x) = 9 x^{2} + 6 x - 12$ betrachtet werden, da x>0.
$\lim_{x \to 0^{+}} (9 x^{2} + 6 x - 12)$ $=$ $- 12$
$\Rightarrow$ Nicht differenzierbar, da $\lim_{x \to 0^{-}} f^{'} (x) \neq \lim_{x \to 0^{+}} f^{'} (x)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme die Nullstellen der Funktion.

Bestimme die Wendepunkte und Art und Lage der Extrempunkte der Funktion.
Untersuche das Symmetrieverhalten des Graphen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
$f (x)$ $=$ $3 \cdot (x^{2} - 4) \cdot (| x | + 1)$
↓
-x für x einsetzen.
$f (- x)$ $=$ $3 \cdot ({(- x)}^{2} - 4) \cdot (| - x | + 1)$
$f (- x)$ $=$ $3 \cdot (x^{2} - 4) \cdot (| x | + 1)$
$f (- x)$ $=$ $f (x)$
$f (- x) = f (x)$ $\Rightarrow$ Achsensymmetrie zur y-Achse
Alle weiteren Informationen findest Du linksoben unter "Was muss ich beachten?"
Hilfe zu den Funktionen des Editors findest Du oben rechts.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

2
Untersuchen einer Betragsfunktion
Gegeben ist die Funktion $f (x) = (3 - | x |) (x + 1)$ .
1. Untersuche $f$ auf Stetigkeit.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stetigkeit
  Beginnen wir mit der Fallunterscheidung.
  $x \geq 0$ bedeutet, $x$ nimmt einen positiven Wert an. Der Betrag ist damit überflüssig und der Funktionsterm ergibt sich zu:
  $f_{x > 0} (x) = (3 - x) (x + 1) = - x^{2} + 2 x + 3$
  $x < 0$ bedeutet, $x$ nimmt einen negativen Wert an. Der Betrag kann dann nur entfernt werden, wenn das Vorzeichen davor wechselt:
  $f_{x < 0} (x) = (3 + x) (x + 1) = x^{2} + 4 x + 3$
  Auf dem Intervall $(- \infty, 0)$ ist $f_{x < 0}$ eine stetige Polynomfunktion. Auf $(0, \infty)$ ist $f_{x > 0}$ ebenfalls stetig. Die Frage ist, was ist mit der Stelle zwischendrin, $x = 0$ ?
  Hierzu betrachte den Grenzwert von links (Welchen Funktionswert hat die Funktion $f_{x < 0}$ in dieser Stelle?):
  $\lim_{x < 0} f_{x < 0} (0) = 0^{2} + 4 \cdot 0 + 3 = 3$
  Hierzu betrachte den Grenzwert von rechts (Welchen Funktionswert hat die Funktion $f_{x > 0}$ in dieser Stelle?):
  $\lim_{x > 0} f_{x > 0} (0) = - 0^{2} + 2 \cdot 0 + 3 = 3$
  Der Funktionswert von $f$ ist:
  $f (0) = (3 - | 0 |) (0 + 1) = 3$
  Alle Werte stimmen überein und die Funktion $f$ ist damit in der Stelle $x = 0$ stetig und sogar insgesamt auf dem ganzen Definitionsbereich.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Mache eine Fallunterscheidung für $x < 0$ und $x > 0$ , wie sieht der Funktionsterm für diese Abschnitte aus? Für die Stetigkeit müssen rechtsseitige und linksseitige Grenzwerte gleich dem Funktionswert sein. Wie sieht das für die Stelle $x = 0$ aus?
2. Untersuche $f$ auf Differenzierbarkeit.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Differenzierbarkeit
  Aus dem ersten Aufgabenteil werden die Funktionen
  $f_{x < 0} (x) = x^{2} + 4 x + 3$
  
  und
  $f_{x > 0} (x) = - x^{2} + 2 x + 3$
  
  aufgegriffen. Die Ableitungen ergeben sich zu:
  $f_{x < 0}^{'} (x) = 2 x + 4$
  $f_{x > 0}^{'} (x) = - 2 x + 2,$
  Diese sind differenzierbar auf ihrem Definitionsbereich, der Knackpunkt ist hier also wieder die Stelle $x_{0} = 0$ . Die linksseitige bzw. rechtsseitige Ableitung in $x_{0} = 0$ ergibt sich zu:
  $\lim_{x < 0} f_{x < 0}^{'} (0) = \lim_{x < 0} 2 \cdot 0 + 4 = 4$
  $\lim_{x > 0} f_{x > 0}^{'} (0) = \lim_{x > 0} - 2 \cdot 0 + 2 = 2$
  Diese Werte stimmen nicht überein, womit die Funktion nicht differenzierbar in $x_{0} = 0$ ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  In welcher Stelle könnte die Funktion nicht differenzierbar sein? Eine Funktion heißt in einer Stelle $x_{0}$ differenzierbar, wenn ihre linksseitige bzw. rechtsseitige Ableitung gleich ist:
  $\lim_{x < 0} f_{x < 0}^{'} (x_{0}) = \lim_{x > 0} f_{x > 0}^{'} (x_{0})$
3. Berechne die Nullstellen und Extrempunkte der Funktion $f$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Nullstellen
  Der Funktionsterm wird $0$ gesetzt: $0 = (3 - | x |) (x + 1)$ , wobei der Term auf der rechten Seite als Produkt formuliert ist. Hier lässt sich direkt der Satz des Nullprodukts anwenden:
  $3 - | x | = 0 \Leftrightarrow x_{1 / 2} = \pm 3 x + 1 = 0 \Leftrightarrow x_{3} = - 1$
  Das Schaubild der Funktion hat drei Nullstellen $N_{1} (- 3 | 0), N_{2} (- 1 | 0), N_{3} (3 | 0)$ .
  Extrema
  Die Funktionen $f_{x < 0} (x), f_{x > 0} (x)$ werden jeweils auf Extrema untersucht, indem die Ableitung $0$ gesetzt wird und die hinreichenden Bedingungen (zweite Ableitung) hinzugezogen werden.
  $f_{x < 0} (x) :$
  $f_{x < 0}^{'} (x) = 2 x + 4$
  $0 = 2 x + 4 \Leftrightarrow x = - 2$
  Da die zweite Ableitung an jeder Stelle $f_{x < 0}^{''} (x) = 2 > 0$ ist, liegt ein Tiefpunkt an dieser Stelle vor. Dieser besitzt die $y$ -Koordinate:
  $f_{x < 0} (- 2) = (- 2)^{2} + 4 \cdot (- 2) + 3 = - 1 \Rightarrow T P (- 2 | - 1)$
  Mehr Extrema kann diese Funktion nicht besitzen.
  $f_{x > 0} (x) :$
  $f_{x > 0}^{'} (x) = - 2 x + 2$
  $0 = - 2 x + 2 \Leftrightarrow x = 1$
  Da die zweite Ableitung an jeder Stelle $f_{x > 0}^{''} (x) = - 2 < 0$ ist, liegt ein Hochpunkt an dieser Stelle vor. Dieser besitzt die $y$ -Koordinate:
  $f_{x > 0} (1) = - 1^{2} + 2 \cdot 1 + 3 = 4 \Rightarrow H P (1 | 4)$
  Mehr Extrema kann diese Funktion nicht besitzen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Funktionen auf den Teilabschnitten $(- \infty, 0)$ und $(0, \infty)$ können einzeln jeweils auf Extrema untersucht werden. Für die Nullstelle lässt sich der Satz des Nullprodukts mit $f$ direkt anwenden.
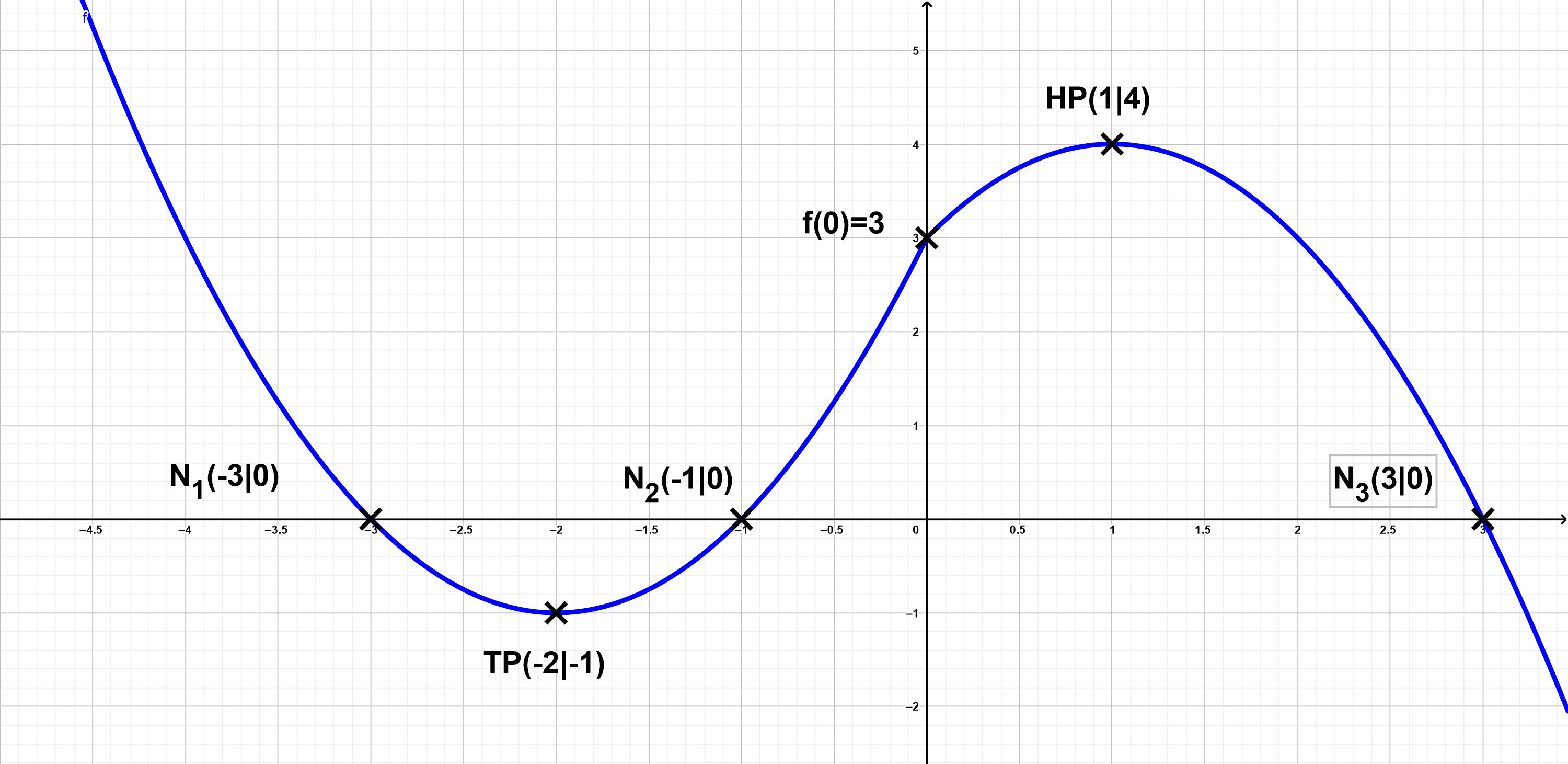
4. Skizziere das Schaubild $G_{f}$ .
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Mithilfe des Aufgabenteils (c) können Punkte in das Koordinatensystem übertragen werden, durch die das Schaubild der Funktion verläuft. Hierbei ist darauf zu achten, dass die Kurve in $x_{0} = 0$ einen Knick aufweist, da sie nach Teil (b) nicht differenzierbar ist.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$f (x)$	$=$	$3 \cdot (x^{2} - 4) (x + 1)$
	↓	Die Klammern ausmultiplizieren.
	$=$	$3 x^{3} + 3 x^{2} - 12 x - 12$

$f (x)$	$=$	$3 \cdot (x^{2} - 4) (- x + 1)$
	↓	Die Klammern ausmultiplizieren.
	$=$	$- 3 x^{3} + 3 x^{2} + 12 x - 12$

$\lim_{x \to 0^{-}} f (x)$	$=$
	↓	Es muss der Term ausgewählt werden, der für x<0 gilt.
	$=$	$\lim_{x \to 0^{-}} (- 3 x^{3} + 3 x^{2} + 12 x - 12)$
	↓	0 einsetzen.
	$=$	$- 12$

$\lim_{x \to 0^{+}} f (x)$	$=$
	↓	Es muss der Term ausgewählt werden, der für x>0 gilt.
	$=$	$\lim_{x \to 0^{+}} (3 x^{3} + 3 x^{2} - 12 x - 12)$
	↓	0 einsetzen.
	$=$	$- 12$

$f (x)$	$=$	$3 x^{3} + 3 x^{2} - 12 x - 12$
	↓	Erste Ableitung bilden.
$f ‘ (x)$	$=$	$9 x^{2} + 6 x - 12$

$\lim_{x \to 0^{-}} (- 9 x^{2} + 6 x + 12)$	$=$	$12$
	↓	Bei Annäherung von rechts, muss $f ‘ (x) = 9 x^{2} + 6 x - 12$ betrachtet werden, da x>0.
$\lim_{x \to 0^{+}} (9 x^{2} + 6 x - 12)$	$=$	$- 12$

$3 \cdot (x^{2} - 4) (x + 1)$	$=$	$0$
	↓	Benutze die 3. Binomische Formel um $x^{2} - 4$ aufzulösen.
$3 \cdot (x + 2) (x - 2) (x + 1)$	$=$	$0$
	↓	Lies die Nullstellen aus den Linearfaktoren ab.
$x_{1}$	$=$	$- 2$
$x_{2}$	$=$	$2$
	↓	Nur $x_{2} = 2$ ist hier eine gültige Lösung, da >0.
$x_{3}$	$=$	$- 1$

$3 \cdot (x^{2} - 4) (- x + 1)$	$=$	$0$
	↓	Benutze die 3. Binomische Formel um $x^{2} - 4$ aufzulösen.
$3 \cdot (x + 2) (x - 2) (- x + 1)$	$=$	$0$
	↓	Lies die Nullstellen aus den Linearfaktoren ab.
$x_{1}$	$=$	$- 2$
	↓	Nur $x_{1} = - 2$ ist hier eine gültige Lösung, da <0.
$x_{2}$	$=$	$2$
$x_{3}$	$=$	$1$

$f (x)$	$=$	$3 \cdot (x^{2} - 4) \cdot (\| x \| + 1)$
	↓	-x für x einsetzen.
$f (- x)$	$=$	$3 \cdot ({(- x)}^{2} - 4) \cdot (\| - x \| + 1)$
$f (- x)$	$=$	$3 \cdot (x^{2} - 4) \cdot (\| x \| + 1)$
$f (- x)$	$=$	$f (x)$

Aufgaben zur Betragsfunktion

Fall x ≥ 0

Fall x<0

Stetigkeit

f(0) berechnen mit Fall x ≥ 0

Annäherung an 0 von links

Annäherung an 0 von rechts

Differenzierbarkeit

Fall: x ≥ 0

Fall: x<0

Fall x=0

Hast du eine Frage oder Feedback?

Fall: x ≥ 0

Fall: x<0

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Untersuchen einer Betragsfunktion

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nullstellen

Extrema

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Fall x $\geq$ 0

f(0) berechnen mit Fall x $\geq$ 0

Fall: x $\geq$ 0

Fall: x $\geq$ 0