Aufgaben zu Berührpunkten an Graphen
Hier findest du gemischte Aufgaben zum Berührpunkt. Lerne, wann sich Graphen berühren und wann sie sich schneiden.
- 1
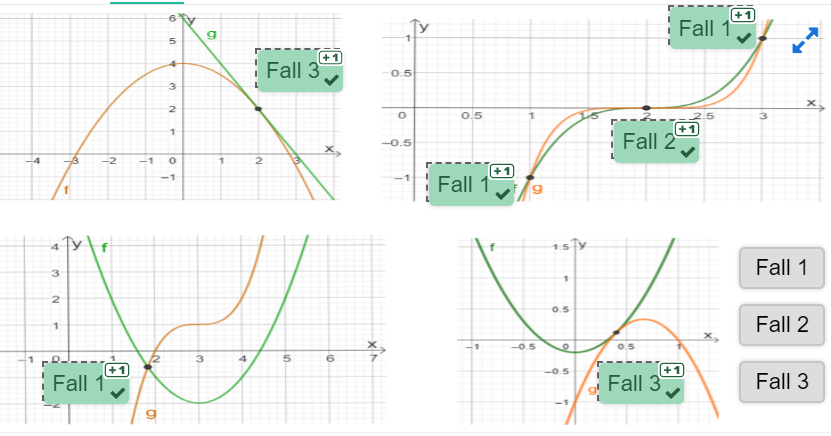
Entscheide jeweils bei den vier Abbildungen, welcher Fall zutrifft.
Fall 1: transversales Schneiden (ein Schnittpunkt mit zwei verschiedenen Tangenten)
Fall 2: berührendes Schneiden (ein Schnittpunkt mit einer gemeinsamen Tangente und die beiden Graphen kreuzen sich im Schnittpunkt)
Fall 3: Berührpunkt (ein Schnittpunkt mit einer gemeinsamen Tangente und die beiden Graphen kreuzen sich nicht im Schnittpunkt)
- 2
Welche Punkte sind Berührpunkte (ein Schnittpunkt mit einer gemeinsamen Tangente und die beiden Graphen kreuzen sich nicht im Schnittpunkt)?
- 3
Gegeben sind die beiden Funktionen und und der Punkt . Zeige, dass ein Berührpunkt der beiden Graphen von und ist.
- 4
Gegeben sind die beiden Funktionsgleichungen , mit und
.
Gib auch die Gleichung der Tangente an.
- 5
Berechne die Koordinaten des Berührpunktes der beiden Parabeln, deren Funktionsgleichungen und gegeben sind:
und .
- 6
Gegeben sind zwei Funktionen und durch:
und
Die Graphen und der beiden Funktionen und haben zwei gemeinsame Punkte und .
Zeige, dass nur einer der beiden Punkte ein Berührpunkt ist.
- 7
An die Funktion soll vom Punkt aus eine Tangente gelegt werden. Bestimme die Gleichung der Tangente und den Berührpunkt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?