Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Gruppe A

Die Aufgaben findest du hier zum Ausdrucken als PDF.

  1. 1

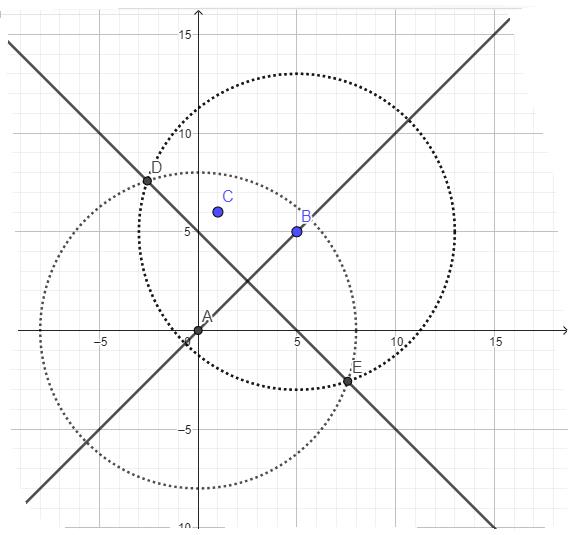
    Die Gerade gg verläuft durch die Punkte AA und BB. Der Punkt CC liegt nicht auf gg (vgl. Abbildung).

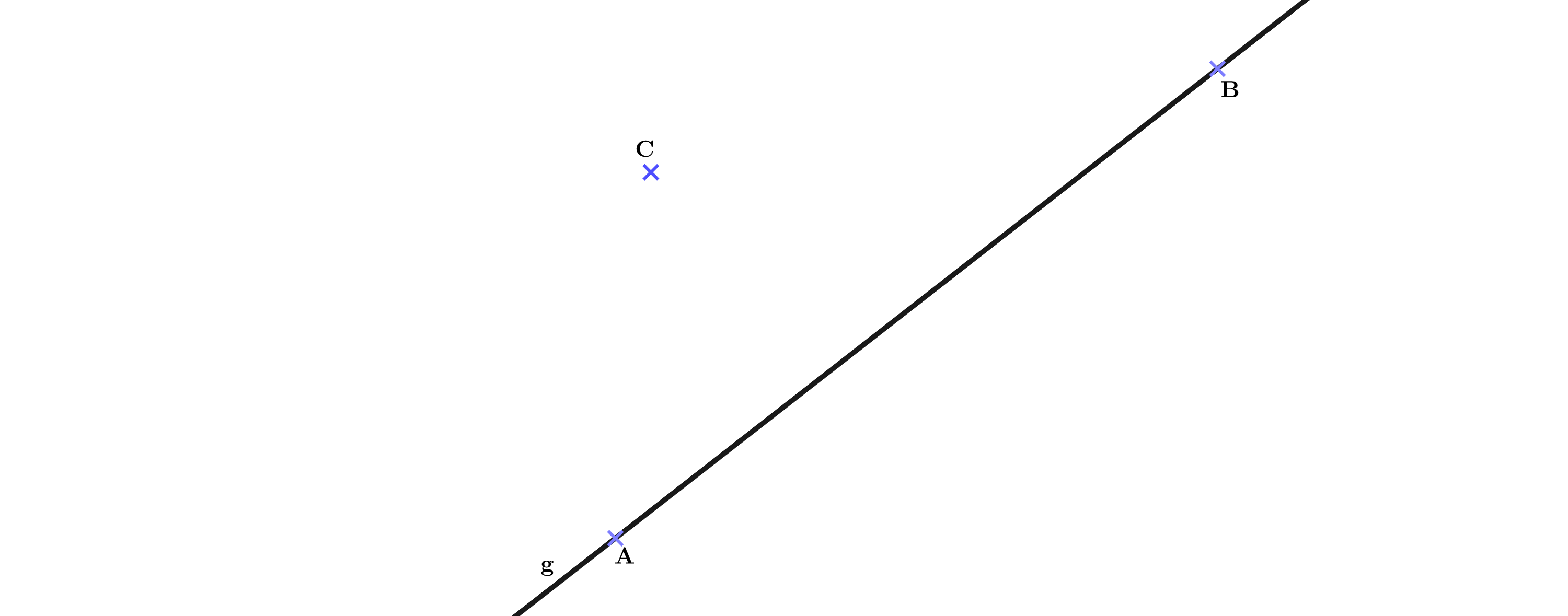
    Hinweis: dies ist im Original eine Aufgabe auf einem Blatt Papier. Wenn du sie bearbeiten möchtest, kannst du in einem Koordinatensystem die Punkte so einzeichnen: , und . Zeichne dann die Gerade durch die Punkte und .

    Hinweis: dies ist im Original eine Aufgabe auf einem Blatt Papier. Wenn du sie bearbeiten möchtest, kannst du in einem Koordinatensystem die Punkte so einzeichnen:

    A(0∣0)A(0∣0), B(5∣5)B(5∣5) und C(1∣6)C(1∣6). Zeichne dann die Gerade gg durch die Punkte AA und BB.

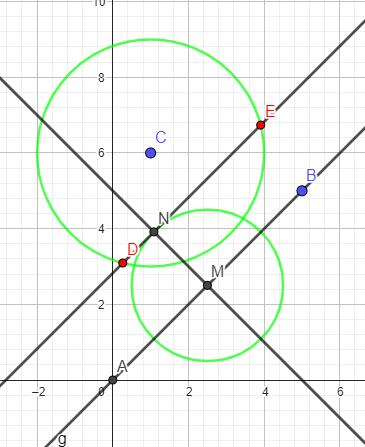
    1. Konstruiere die Mittelsenkrechte der Strecke AB‾\overline{AB}.

    2. Vervollständige, sodass eine wahre Aussage entsteht.

      Der Abstand des Punkts CC zur Gerade gg ist die Länge der Strecke CS‾\overline{CS}, wobei SS der Schnittpunkt von gg und _______________________ ist.

    3. Ermittle diejenigen Punkte, die von gg den Abstand 2 cm2~\text{cm} haben und zugleich von CC genau 3 cm3~\text{cm} entfernt sind. Markiere diese Punkte farbig.

  2. 2

    Bestimme die Lösung der Gleichung 23=16+18x\ \dfrac{2}{3}=\dfrac{1}{6}+\dfrac{1}{8}\text{x}

  3. 3

    Die abgebildete Tabelle wurde mit einem

    Tabellenkalkulationsprogramm erstellt.

    Gib den Wert an, der durch die Formel in der Zelle B2\mathrm{B2}

    berechnet wird

    A\text{A}

    B\hspace{9mm}\text{B}

    1

    2\mathrm{2}

    2

    7\mathrm{7}

    =A1∗(A2−3)\mathrm{=A1*(A2-3)}

  4. 4

    Löse folgende Aufgaben.

    1. Susanne sagt: „Wenn ich den Wert des Terms 13⋅84+87⋅84\mathrm{13\cdot84+87\cdot84} berechnen soll, ergibt sich durch die Verwendung des Distributivgesetzes ein Rechenvorteil.“ Erkläre den Rechenvorteil anhand des Terms.

    2. Vereinfache folgenden Term so weit wie möglich:

      3a⋅(1−2a)+7a2=\qquad \mathrm{3a\cdot (1-2a)+7a^2=}

  5. 5

    In einer Umfrage mussten Erwachsene angeben, mit welcher Schulnote sie ihre Mathematikkenntnisse selbst einschätzen würden.

    Das untenstehende Säulendiagramm zeigt die Anteile der einzelnen Noten.

    Bild

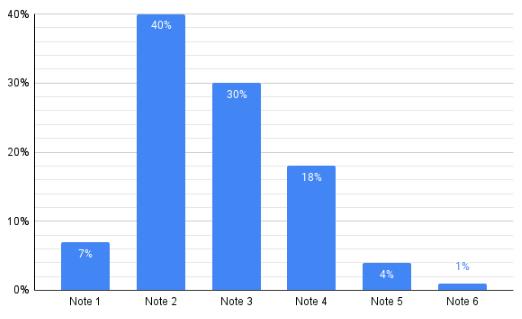
    1. Beurteile, ob folgende Aussage mit dem Diagramm in Einklang steht:

      Jeder Zwanzigste der Befragten schätzt seine Mathematikkenntnisse schlechter als Note 4 ein.

    2. Die Daten sollen als Kreisdiagramm dargestellt werden. Berechne die Größe des Winkels für den Sektor „Note 22“.

    3. Gib einen Term an, mit dem sich die Durchschnittsnote der Selbsteinschätzungen berechnen lässt.

    4. Bestimme die Gesamtzahl der Befragten unter der Annahme, dass genau 300300 der Befragten ihre Mathematikkenntnisse mit Note 33 einstuften.

  6. 6

    Löse folgende Aufgaben:

    1. Gib 2,5 h\mathrm{2{,}5\ h} in Minuten an.

    2. Von den folgenden Darstellungen beschreiben genau zwei das gleiche Volumen wie 0,2 dm3\mathrm{0{,}2\ dm^3}. Kreuze (nur) diese beiden an.

  7. 7

    Untenstehende nicht maßstabsgetreue Abbildung zeigt die parallelogrammförmige Seitenfläche eines Treppengeländers.

    Bild

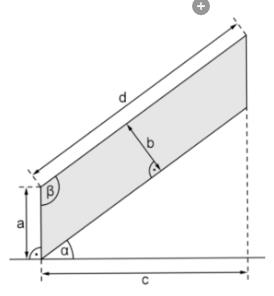
    1. Berechne die Größe des Winkels ββ, wenn der Neigungswinkel αα der Treppe gegenüber der Horizontalen 34°34° beträgt.

    2. Berechne den Inhalt der Seitenfläche für b=0,8 m \mathrm{b=0{,}8\ m}\ und d=4 m.\mathrm{d=4\ m}.

    3. Begründe mithilfe von Überlegungen zum Flächeninhalt des Parallelogramms, dass sich die Länge c\text{c} mit der Gleichung  c=b⋅da \ \mathrm{c=\dfrac{b\cdot d}{a}}\ berechnen lässt, wenn a, b \text{a, b}\ und d\text{d} bekannt sind.


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?