Wahlteil - GTR - lernen mit Serlo!

Aufgabe 3A

Betrachtet werden die Pyramiden $A B C D S_{k}$

mit $A (0 | 0 | 0), B (2 | 0 | 0), C (2 | 2 | 0), D (0 | 2 | 0)$ und $S_{k} (1 | 1 | k)$ mit $k > 1$ .

Die gemeinsame Grundfläche $A B C D$ dieser Pyramiden ist quadratisch. Der Schnittpunkt der Diagonalen der Grundfläche $A B C D$ wird mit $T$ bezeichnet.

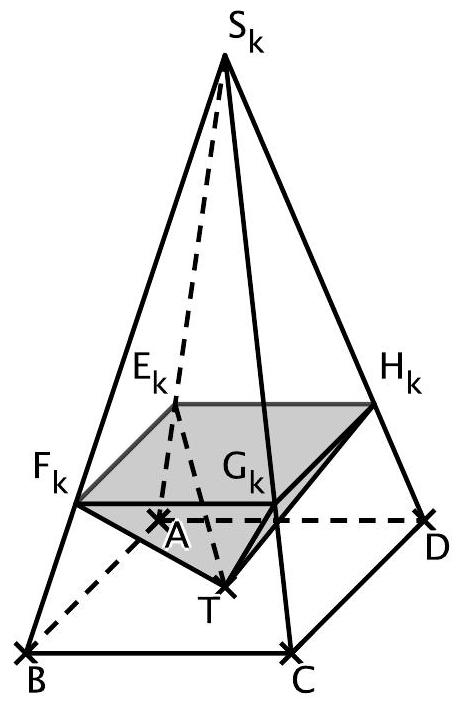
Die Abbildung zeigt beispielhaft eine dieser Pyramiden.

Berechnen Sie den Inhalt der Oberfläche der Pyramide $A B C D S_{k}$ . (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Inhalt der Oberfläche der Pyramide $A B C D S_{k}$
$O_{Pyramide} = G + 4 \cdot A_{△}$
Dabei ist $G = 2^{2} = 4$ und $A_{△} = \frac{1}{2} \cdot g \cdot h$
Die Grundseite des Dreiecks ist $g = 2.$
Die Mitte der Seite $B C$ ist der Punkt $M$ .
$\Rightarrow \vec{m} = \frac{1}{2} \cdot ((\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) + (\begin{array}{c} 2 \\ 2 \\ 0 \end{array})) = (\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) \Rightarrow M (2 | 1 | 0)$
Der Vektor $\vec{M S_{k}} = (\begin{array}{c} 1 \\ 1 \\ k \end{array}) - (\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} - 1 \\ 0 \\ k \end{array})$
Die Dreieckshöhe ist $h = | \vec{M S_{k}} | = \sqrt{(- 1)^{2} + k^{2}} = \sqrt{1 + k^{2}} .$
Dann folgt für den Inhalt der Pyramidenoberfäche:
$O_{Pyramide} = G + 4 \cdot A_{△} = 4 + 4 \cdot \frac{1}{2} \cdot 2 \cdot \sqrt{1 + k^{2}} = 4 + 4 \cdot \sqrt{1 + k^{2}}$
.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es ist $O_{Pyramide} = G + 4 \cdot A_{△}$
Für die Dreiecksfläche benötigst Du die Dreieckshöhe, für die gilt, $h = | \vec{M S_{k}} |$ , mit dem Punkt $M$ als Mitte der Seite $B C$ .
Der Punkt $S_{k}$ wird am Punkt $C$ gespiegelt. Geben Sie die Koordinaten des Spiegelpunktes zu $S_{k}$ an.
Berechnen Sie den Wert von $k$ so, dass $S_{k}$ zu seinem Spiegelpunkt den Abstand 6 hat.
(4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung Punkt an Punkt
Koordinaten des Spiegelpunktes $S_{k}$ '
Für den Spiegelpunkt gilt:
$\vec{O S_{k}^{'}} = \vec{O S_{k}} + 2 \cdot \vec{S_{k} C} = (\begin{array}{c} 1 \\ 1 \\ k \end{array}) + 2 \cdot ((\begin{array}{c} 2 \\ 2 \\ 0 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ k \end{array})) = (\begin{array}{c} 3 \\ 3 \\ - k \end{array})$
Der Spiegelpunkt hat die Koordinaten $S_{k}^{'} (3 | 3 | - k)$ .
Abstand von $S_{k}$ zu $S_{k}^{'}$ beträgt 6
$\vec{S_{k} S_{k}^{'}} = (\begin{array}{c} 3 \\ 3 \\ - k \end{array}) - (\begin{array}{c} 1 \\ 1 \\ k \end{array}) = (\begin{array}{c} 2 \\ 2 \\ - 2 k \end{array})$
$| \vec{S_{k} S_{k}^{'}} | = \sqrt{2^{2} + 2^{2} + (- 2 k)^{2}} = \sqrt{8 + 4 k^{2}}$
Nun soll gelten: $\sqrt{8 + 4 k^{2}} = 6$
Der GTR liefert als Lösung $k_{1} \approx - 2,64575...$ und $k_{2} \approx 2,64575...$ .
Da $k > 1$ ist, erhält man als Lösung der Gleichung nur den positiven Wert $k \approx 2,65$ .
Für $k \approx 2,65$ hat $S_{k}$ zu seinem Spiegelpunkt den Abstand $6$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Es gilt für den Spiegelpunkt: $\vec{O S_{k}^{'}} = \vec{O S_{k}} + 2 \cdot \vec{S_{k} C}$
Teil 2
Es soll gelten: $| \vec{S_{k} S_{k}^{'}} | = 6$ . Löse nach $k$ auf.
Die Seitenfläche $A B S_{k}$ liegt in der Ebene $L$ .
Bestimmen Sie eine Gleichung von $L$ in Koordinatenform. (3 BE)
[zur Kontrolle: $k \cdot y - z = 0]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Überblick
Gleichung von $L$ in Koordinatenform
$\vec{A B} = (\begin{array}{c} 2 \\ 0 \\ 0 \end{array})$ und $\vec{A S_{k}} = (\begin{array}{c} 1 \\ 1 \\ k \end{array})$
Es soll gelten:
$\vec{n} \circ \vec{A B} = 0$ und $\vec{n} \circ \vec{A S_{k}} = 0$
1. Gleichung: $(\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array}) \circ (\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) = 0 \Rightarrow 2 \cdot n_{1} + 0 + 0 = 0 \Rightarrow n_{1} = 0$
2. Gleichung: $(\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array}) \circ (\begin{array}{c} 1 \\ 1 \\ k \end{array}) = 0$
Mit $n_{1} = 0$ erhält man die Gleichung: $n_{2} + k \cdot n_{3} = 0$
Wähle z.B. $n_{3} = - 1,$ dann folgt: $n_{2} - k = 0 \Rightarrow n_{2} = k$ .
Der Normalenvektor lautet demnach: $\vec{n} = (\begin{array}{c} 0 \\ k \\ - 1 \end{array})$
Da die Ebene $L$ den Koordinatenursprung $A (0 | 0 | 0)$ enthält, gilt für die Ebenengleichung: $L : k \cdot y - z = 0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es gilt: $\vec{n} \circ \vec{A B} = 0$ und $\vec{n} \circ \vec{A S_{k}} = 0$ . Berechne den Normalenvektor $\vec{n} .$
Beachte $L$ verläuft durch den Koordinatenursprung.
Bestimmen Sie denjenigen Wert von $k$ , für den die Seitenfläche $A B S_{k}$ gegenüber der Grundfläche $A B C D$ um einen Winkel der Größe $60^{\circ}$ geneigt ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
Größe von $k$
Der Normalenvektor der Grundfläche $A B C D$ ist der Normalenvektor der xy-Ebene:
${\vec{n}}_{x y} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ . Sein Betrag ist $| \vec{n} | = 1$ .
Der Normalenvektor der Seitenfläche ist ${\vec{n}}_{L} = (\begin{array}{c} 0 \\ k \\ - 1 \end{array})$ .
Sein Betrag ist $| {\vec{n}}_{L} | = \sqrt{k^{2} + 1}$ .
Dann gilt für den Winkel: $\cos 60^{\circ} = \frac{| {\vec{n}}_{x y} \circ {\vec{n}}_{L} |}{| {\vec{n}}_{x y} | \cdot | {\vec{n}}_{L} |}$
$\cos 60^{\circ}$ $=$ $\frac{| (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) \circ (\begin{array}{c} 0 \\ k \\ - 1 \end{array}) |}{1 \cdot \sqrt{k^{2} + 1}}$
↓
Berechne das Skalarprodukt und den $\cos 60^{\circ}$ .
$0,5$ $=$ $\frac{| - 1 |}{1 \cdot \sqrt{k^{2} + 1}}$
↓
Berechne den Betrag.
$0,5$ $=$ $\frac{1}{\sqrt{k^{2} + 1}}$
Der GTR liefert als Lösung $k_{1} \approx - 1,73205...$ und $k_{2} \approx 1,73205...$ .
Da $k > 1$ ist, erhält man als Lösung nur den positiven Wert $k \approx 1,73205...$ .
Für $k \approx 1,73$ bilden die beiden Ebenen einen Winkel von $60^{\circ}$ miteinander.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Normalenvektor der Grundfläche $A B C D$ ist der Normalenvektor der xy-Ebene: ${\vec{n}}_{x y} = (\begin{array}{c} 0 \\ 0 \\ 1 \end{array})$ .
Der Normalenvektor ${\vec{n}}_{L}$ der Seitenfläche wurde in Aufgabe c) berechnet.
Dann gilt für den Winkel: $\cos 60^{\circ} = \frac{| {\vec{n}}_{x y} \circ {\vec{n}}_{L} |}{| {\vec{n}}_{x y} | \cdot | {\vec{n}}_{L} |}$ . Löse die Gleichung nach $k$ auf.
Untersuchen Sie, ob es einen Wert für $k > 1$ gibt, sodass das Dreieck $B S_{k} D$ rechtwinklig ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Dreieck $B S_{k} D$ soll rechtwinklig sein
Berechne die Vektoren $\vec{B S_{k}}$ und $\vec{D S_{k}}$ und setze dann ihr Skalarprodukt gleich null.
$\vec{B S_{k}} = (\begin{array}{c} 1 \\ 1 \\ k \end{array}) - (\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} - 1 \\ 1 \\ k \end{array})$
$\vec{D S_{k}} = (\begin{array}{c} 1 \\ 1 \\ k \end{array}) - (\begin{array}{c} 0 \\ 2 \\ 0 \end{array}) = (\begin{array}{c} 1 \\ - 1 \\ k \end{array})$
$\vec{B S_{k}} \circ \vec{D S_{k}} = 0 \Rightarrow (\begin{array}{c} - 1 \\ 1 \\ k \end{array}) \circ (\begin{array}{c} 1 \\ - 1 \\ k \end{array}) = 0$
Man erhält die Gleichung:
$- 1 - 1 + k^{2} = 0 \Rightarrow k^{2} = 2$
Da $k > 1$ ist , erhält man als Lösung der Gleichung $k^{2} = 2$ nur den positiven Wert $k = \sqrt{2}$ .
Für $k = \sqrt{2}$ ist das Dreieck $B S_{k} D$ rechtwinklig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Vektoren $\vec{B S_{k}}$ und $\vec{D S_{k}}$ und setze dann ihr Skalarprodukt gleich null. Löse die Gleichung nach $k$ auf.
Die Ebene mit der Gleichung $z = 1$ schneidet die vier vom Punkt $S_{k}$ ausgehenden Kanten der Pyramide $A B C D S_{k}$ in den Punkten $E_{k}, F_{k}, G_{k}$ und $H_{k}$ (vgl. Abbildung).
Bestimmen Sie die $x$ - und die $y$ -Koordinate von $F_{k}$ . (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
Die $x$ - und die $y$ -Koordinate von $F_{k}$
Der Punkt $F$ hat wegen $z = 1$ die Koordinaten $F (x | y | 1)$ .
Die Gerade durch die Punkte $B$ und $S_{k}$ hat die Gleichung:
$g_{B S_{k}} : \vec{x} = \vec{O B} + r \cdot \vec{B S_{k}} = (\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ k \end{array})$
Der Punkt $F$ liegt auf dieser Geraden:
$\Rightarrow (\begin{array}{c} 2 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ k \end{array}) = (\begin{array}{c} x \\ y \\ 1 \end{array})$
Aus Gleichung $(I I I)$ folgt dann $r = \frac{1}{k}$ .
$r = \frac{1}{k}$ eingesetzt liefert die x- und y-Koordinaten: $x = 2 - \frac{1}{k}$ und $y = \frac{1}{k}$ .
Damit hat der Punkt $F$ die Koordinaten $F (2 - \frac{1}{k} | \frac{1}{k} | 1)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Punkt $F$ hat wegen $z = 1$ die Koordinaten $F (x | y | 1)$ .
Erstelle die Gleichung der Geraden durch die Punkte $B$ und $S_{k}$ .
Setze in die Geradengleichung die Koordinaten von $F$ ein.
Bestimmen Sie diejenigen Werte von $k$ , für die das Verhältnis des Volumens der Pyramide $E_{k} F_{k} G_{k} H_{k} T$ zum Volumen der Pyramide $A B C D S_{k} \frac{1}{8}$ beträgt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz (Vierstreckensatz)
Verhältnis des Volumens der Pyramide $E_{k} F_{k} G_{k} H_{k} T$ zum Volumen der Pyramide $A B C D S_{k}$
Das Pyramidenvolumen ist $V = \frac{1}{3} \cdot G \cdot h$ .
Die Dreiecke $A B S_{k}$ und $E_{k} F_{k} S_{k}$ sind ähnlich.
$S_{k}$ hat die z-Koordinate $z = k$ .
Ein Punkt im Viereck $E_{k} F_{k} G_{k} H_{k}$ hat die z-Koordinate $z = 1$ .
Dann gilt mit dem Strahlensatz:
$\Rightarrow \frac{| E_{k} F_{K} |}{| A B |} = \frac{k - 1}{k}$
Das Verhältnis der beiden Pyramidenvolumina soll $\frac{1}{8}$ betragen:
$\frac{V_{E_{k} F_{k} G_{k} H_{k} T}}{V_{A B C D S_{k}}} = \frac{1}{8} \Rightarrow \frac{\frac{1}{3} \cdot | E_{k} F_{K} |^{2} \cdot 1}{\frac{1}{3} \cdot | A B |^{2} \cdot k} = \frac{1}{8} \Rightarrow {(\frac{| E_{k} F_{K} |}{| A B |})}^{2} \cdot \frac{1}{k} = \frac{1}{8}$
Nach Kürzen mit $\frac{1}{3}$ und Einsetzen von $\frac{| E_{k} F_{K} |}{| A B |} = \frac{k - 1}{k}$ folgt:
${(\frac{k - 1}{k})}^{2} \cdot \frac{1}{k} = \frac{1}{8}$
Der GTR liefert die Lösungen $k_{1} \approx 0,764$ , $k_{2} = 2$ und $k_{3} \approx 5,24$ erhalten.
Die Lösung $k_{1}$ entfällt, da $k > 1$ sein muss.
Für $k = 2$ oder $k \approx 5,24$ beträgt das Verhältnis der beiden Pyramidenvolumina $\frac{1}{8}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Es soll gelten: $\frac{V_{E_{k} F_{k} G_{k} H_{k} T}}{V_{A B C D S_{k}}} = \frac{1}{8}$
Die Dreiecke $A B S_{k}$ und $E_{k} F_{k} S_{k}$ sind ähnlich.
$S_{k}$ hat die z-Koordinate $z = k$ und ein Punkt im Viereck $E_{k} F_{k} G_{k} H_{k}$ hat die z-Koordinate $z = 1$ .
Wende den Strahlensatz auf die Seiten $E_{k} F_{K}$ und $A B$ an.
Das Volumenverhältnis liefert dann eine Gleichung für $k$ .

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

$\cos 60^{\circ}$	$=$	$\frac{\| (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) \circ (\begin{array}{c} 0 \\ k \\ - 1 \end{array}) \|}{1 \cdot \sqrt{k^{2} + 1}}$
	↓	Berechne das Skalarprodukt und den $\cos 60^{\circ}$ .
$0,5$	$=$	$\frac{\| - 1 \|}{1 \cdot \sqrt{k^{2} + 1}}$
	↓	Berechne den Betrag.
$0,5$	$=$	$\frac{1}{\sqrt{k^{2} + 1}}$

Aufgabe 3A

Inhalt der Oberfläche der Pyramide ABCDSk

Hast du eine Frage oder Feedback?

Koordinaten des Spiegelpunktes Sk'

Abstand von Sk zu Sk′ beträgt 6

Hast du eine Frage oder Feedback?

Gleichung von L in Koordinatenform

Hast du eine Frage oder Feedback?

Größe von k

Hast du eine Frage oder Feedback?

Das Dreieck BSkD soll rechtwinklig sein

Hast du eine Frage oder Feedback?

Die x - und die y-Koordinate von Fk

Hast du eine Frage oder Feedback?

Verhältnis des Volumens der Pyramide EkFkGkHkT zum Volumen der Pyramide ABCDSk

Hast du eine Frage oder Feedback?

Inhalt der Oberfläche der Pyramide $A B C D S_{k}$

Koordinaten des Spiegelpunktes $S_{k}$ '

Abstand von $S_{k}$ zu $S_{k}^{'}$ beträgt 6

Gleichung von $L$ in Koordinatenform

Größe von $k$

Das Dreieck $B S_{k} D$ soll rechtwinklig sein

Die $x$ - und die $y$ -Koordinate von $F_{k}$

Verhältnis des Volumens der Pyramide $E_{k} F_{k} G_{k} H_{k} T$ zum Volumen der Pyramide $A B C D S_{k}$