Wahlteil - GTR - lernen mit Serlo!

Aufgabe 1B

Die Grafik stellt den Schuldenstand Deutschlands in Mrd. Euro jeweils zu Beginn des Jahres ab dem Jahr 1950 dar.

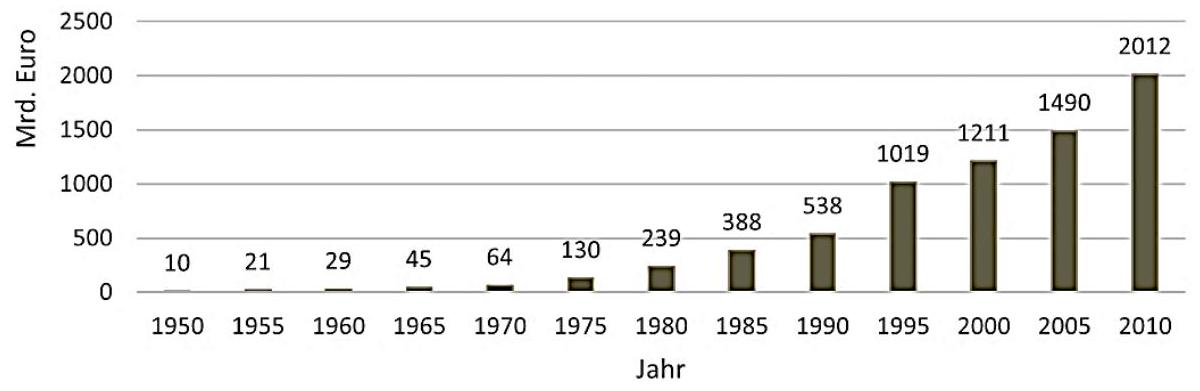
Geben Sie die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Diagramme erfassen und auswerten
Fünfjahreszeiträume
Dem Diagramm entnimmt man die erste Jahreszahl $1950$ mit $10$ Milliarden €.
$1955$ hat sich der Schuldenstand auf $21$ Milliarden € erhöht, also etwas mehr als verdoppelt.
Im weiteren Verlauf findet man dann das Jahr $1970$ mit $64$ Milliarden € und nach $5$ Jahren, also $1975$ einen Schuldenstand von $130$ Milliarden €, also etwas mehr als verdoppelt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte benachbarte Datensätze, bei denen einer etwa doppelt so groß wie der vorherige ist.
Bestimmen Sie zwei geeignete Regressionsfunktionen.
Beurteilen Sie die von Ihnen gewählten Regressionsfunktionen hinsichtlich ihrer Eignung zur Beschreibung des vorliegenden Sachverhalts. (9 BE)
Exponentielle Regression
Wähle z.B. die exponentielle Regression $y = a \cdot e^{b \cdot x}$ .
Übertrage alle Daten in eine Tabelle und lass Dir die entsprechenden Koeffizienten anzeigen.
Der TR liefert die Werte $a \approx 1,15085 \cdot 10^{- 76}$ und $b \approx 1,09522$
$\Rightarrow y = 1,15085 \cdot 10^{- 76} \cdot e^{1,09522 \cdot x}$
Ergebnis ist eine klassische e-Funktion mit unbegrenztem Schuldenwachstum. Es findet keine Schuldenbremse statt.
Logistische Regression
Wähle als weitere Möglichkeit die logistische Regression $y = \frac{c}{1 + a \cdot e^{- b \cdot x}}$ .
Der TR liefert die Werte $c \approx 2938,15971$ , $a \approx 4,33448 \cdot 10^{89}$ und $b \approx 0,10303$
$\Rightarrow y = \frac{2938,15971}{1 + 4,33448 \cdot 10^{89} \cdot e^{- 0,10303 \cdot x}}$
Ergebnis ist eine sich abflachende e-Funktion, die geeignet ist, den Schuldenstand mit einer Schuldenbremse darzustellen.
Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.
Sie dient nur der Veranschaulichung.
Die blauen Punkte sind der gegebene Datensatz. Der grüne Graph entspricht der exponentiellen Regression und der orangefarbige Graph der logistischen Regression.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Übertrage die Daten in eine Tabelle.
Wähle z.B. die exponentielle Regression $y = a \cdot e^{b \cdot x}$ .
Wähle als weitere Möglichkeit die logistische Regression $y = \frac{c}{1 + a \cdot e^{- b \cdot x}}$
Lasse Dir vom TR die entsprechenden Parameter ausrechnen und interpretiere beide Ergebnisse bezüglich einer möglichen Schuldenbremse.
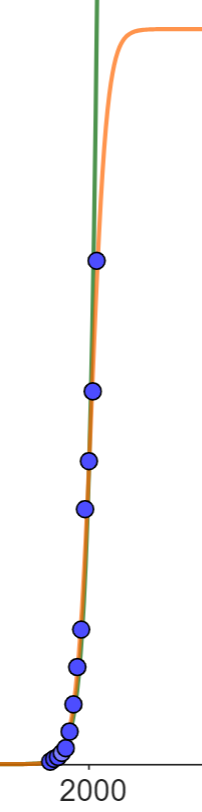
In einem Modell soll der Anstieg des Schuldenstands gestoppt werden und die Schulden sollen abgebaut werden. Zu Beginn des Jahres 2005 beträgt der Schuldenstand in diesem Modell 1490 Mrd. Euro. Die Änderungsrate des Schuldenstands soll ab Beginn des Jahres 2005 durch die Funktion $g$ mit $g (x) = 235 \cdot e^{- 0,25 x} - 35$ , $x$ in Jahren ab dem Jahr 2005, $g (x)$ in Mrd. Euro pro Jahr, beschrieben werden. Die Abbildung zeigt den Graphen der Funktion $g$ . Eine Stammfunktion zu $g$ lautet:
$G (x) = - 940 \cdot e^{- 0,25 x} - 35 \cdot x$
Begründen Sie, dass der nach diesem Modell erwartete Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 mit dem folgenden Term bestimmt werden kann: (3 BE)
$1490 + \int_{0}^{20} g (x) d x$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 kann mit dem folgenden Term bestimmt werden: $1490 + \int_{0}^{20} g (x) d x$
Die Funktion $𝑔$ gibt die Änderung des Schuldenstands in Milliarden € pro Jahr an.
Das Integral von $𝑔$ über ein Zeitintervall gibt die Gesamtzunahme der
Schulden in dem entsprechenden Zeitraum an.
$1490$ Milliarden € ist der Schuldenstand zu Beginn des Jahres $2005$ .
Das Integral geht von $0$ (entspricht dem Jahr $2005$ ) bis $20$ (entspricht dem Jahr $2025$ ).
Die Summe von $1490$ und dem Integral gibt demnach den Schuldenstand zu Beginn des Jahres $2025$ an.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Funktion $𝑔$ gibt die Änderung des Schuldenstands in Milliarden € pro Jahr an.
Das Integral von $𝑔$ über ein Zeitintervall gibt die Gesamtzunahme der Schulden in dem entsprechenden Zeitraum an.
Interpretiere dann die angegebene Summe.
Skizzieren Sie in das Koordinatensystem den nach diesem Modell ungefähr zu erwartenden Schuldenstand vom Beginn des Jahres 2005 bis zum Jahr 2045. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Skizze des Koordinatensystems
Der Schnittpunkt mit der y-Achse liegt bei $1490$ .
Der Hochpunkt liegt an der Stelle der Nullstelle des Graphen von $𝑔$ .
Nach dem Hochpunkt erfolgt annähernd eine lineare Abnahme.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Schnittpunkt mit der y-Achse liegt bei $1490$ .
Der Hochpunkt liegt an der Stelle der Nullstelle des Graphen von $𝑔$ .
Nach dem Hochpunkt erfolgt annähernd eine lineare Abnahme.
Berechnen Sie für dieses Modell das Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005. (4 BE)
Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005
Definiere die Funktion $f (x) = 1490 + \int_{0}^{t} g (x) d x$
Löse dann die Gleichung $f (x) = 1490$ :
$1490 + \int_{0}^{t} g (x) d x = 1490 \Rightarrow \int_{0}^{t} g (x) d x = 0$
Der GTR liefert als Lösung $t \approx 26,824284...$ .
Das Ergebnis ist $t \approx 26,8$ Jahre, d.h. wir sind dann im Jahr $2005 + 26,8 = 2031,8$ .
Im Jahr $2031$ ist der zu erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres $2005$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Definiere die Funktion $f (x) = 1490 + \int_{0}^{t} g (x) d x$
Löse dann die Gleichung $f (x) = 1490$ .
Bestimmen Sie den maximalen Schuldenstand sowie das Jahr, in dem dieser erreicht wird. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
Maximaler Schuldenstand sowie das Jahr, in dem dieser erreicht wird
Der Schuldenstand ist maximal, wenn die Änderungsrate gleich null ist.
$g (x) = 235 \cdot e^{- 0.25 x} - 35 = 0$
Der GTR liefert als Lösung dieser Gleichung den Wert $x \approx 7,616949...$ .
Das Ergebnis ist $x \approx 7,62$ Jahre.
Wir sind dann im Jahr $2005 + 7,62 = 2012,62$ .
Im Jahr $2012$ ist der zu erwartete Schuldenstand maximal.
Er beträgt $f (7,62) = 1490 + \int_{0}^{7,62} g (x) d x \approx 2023,4$
Der maximale Schuldenstand beträgt etwa $2023,4$ Milliarden €.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für das Jahr des maximalen Schuldenstandes berechne $g (x) = 0 \Rightarrow x_{1} .$
Für den maximalen Schuldenstand berechne $f (x_{1}) = 1490 + \int_{0}^{x_{1}} g (x) d x .$
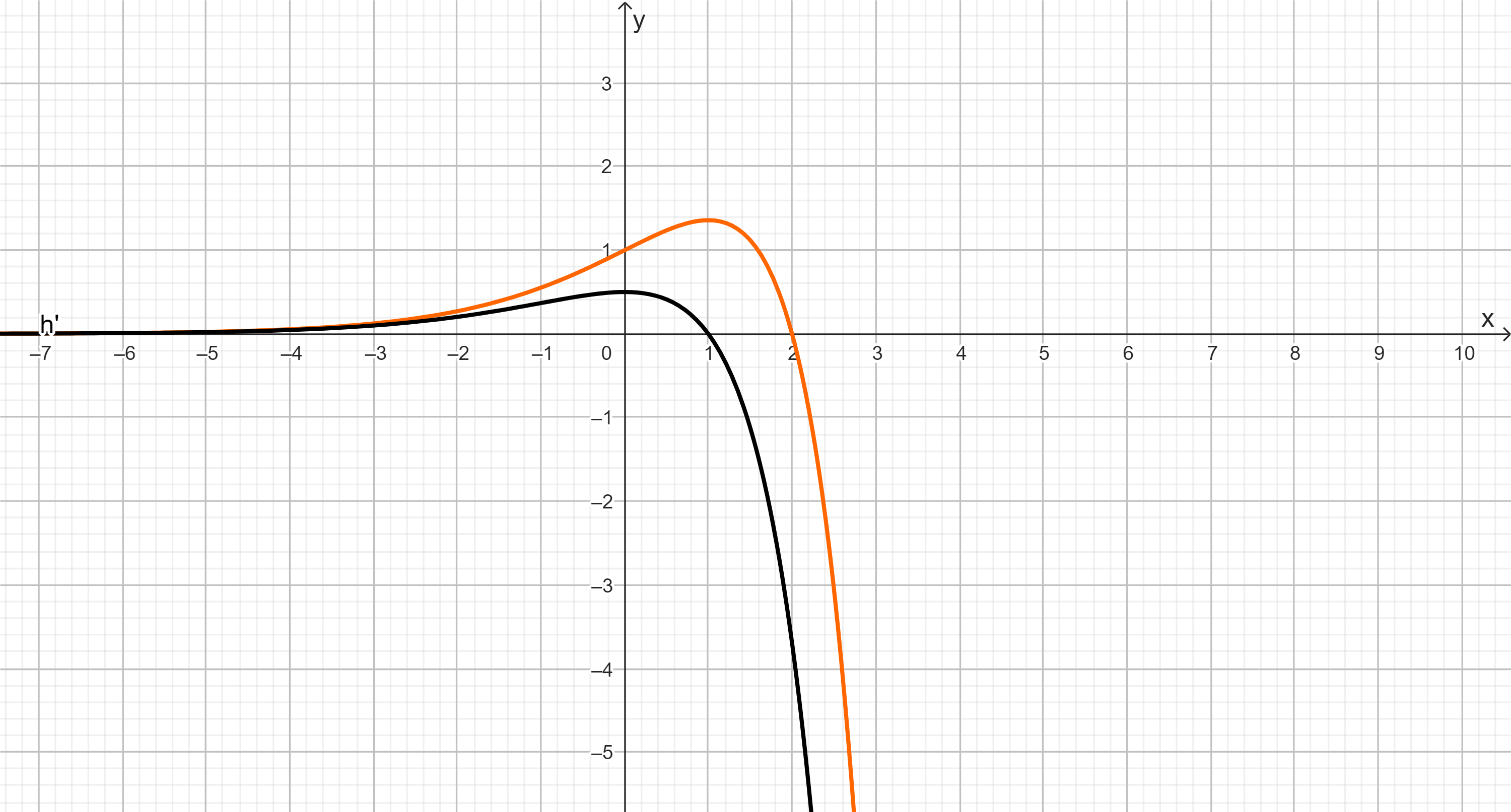
Unabhängig vom Sachkontext ist die in $ℝ$ definierte Funktionenschar $h_{a}$ mit $h_{a} (x) = (1 - a \cdot x) \cdot e^{2 \cdot a \cdot x}, a \in ℝ$ , gegeben.
Ohne weiteren Nachweis können Sie verwenden: $h_{a}^{'} (x) = a \cdot (1 - 2 \cdot a \cdot x) \cdot e^{2 \cdot a \cdot x}$
Zeigen Sie für $a \neq 0$ , dass der maximale Funktionswert unabhängig vom Wert von $a$ ist.
(4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
Nachweis für $a \neq 0$ , dass der maximale Funktionswert unabhängig vom Wert von $a$ ist
Setze $h_{a}^{'} (x) = 0 \Rightarrow 0 = a \cdot (1 - 2 a x) \cdot e^{2 a x}$
Mit dem Satz vom Nullprodukt folgt dann, dass $1 - 2 a x = 0$ sein muss, da $a \neq 0$ und $e^{2 a x} > 0$ für alle $x$ ist.
$1 - 2 a x = 0 \Rightarrow x = \frac{1}{2 a}$
Berechne den maximalen Funktionswert an der Stelle $x = \frac{1}{2 a}$ :
$h_{a} (x)$ $=$ $(1 - a \cdot x) \cdot e^{2 \cdot a \cdot x}$
↓
Setze $x = \frac{1}{2 a}$ ein.
$h_{a} (\frac{1}{2 a})$ $=$ $(1 - a \cdot \frac{1}{2 a}) e^{2 a \cdot \frac{1}{2 a}}$
↓
Kürze mit $a$ .
$=$ $(1 - \frac{1}{2}) e^{\frac{2}{2}}$
↓
Fasse zusammen.
$=$ $\frac{1}{2} \cdot e^{1}$
Der maximale Funktionswert $h_{a} (x) = \frac{1}{2} \cdot e$ ist unabhängig von $a$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze $h_{a}^{'} (x) = 0 \Rightarrow x_{1}$
Berechne $h_{a} (x_{1})$ .
Für jeden Wert von $a$ für $a \neq 0$ wird die Gerade durch den Schnittpunkt mit der $x$ -Achse und den Hochpunkt des zugehörigen Graphen zu $h_{a}$ betrachtet.
Für alle diese Geraden gilt: Sie schneiden sich in einem Punkt auf der $y$ -Achse.
Bestimmen Sie die $y$ -Koordinate dieses gemeinsamen Punktes auch mithilfe einer Skizze ohne Berechnung der Geradengleichungen. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz (Vierstreckensatz)
y-Koordinate dieses gemeinsamen Punktes mithilfe einer Skizze ohne Berechnung der Geradengleichungen
Die Gerade geht durch den Schnittpunkt mit der $x$ -Achse und den Hochpunkt $H P (\frac{1}{2 a} | \frac{1}{2} e)$ des zugehörigen Graphen zu $h_{a}$ .
Benötigt wird der Schnittpunkt mit der $x$ -Achse.
Berechne $h_{a} (x) = 0$
$0 = (1 - a x) \cdot e^{2 \cdot a \cdot x}$
Wegen $e^{2 a x} > 0$ für alle $x$ , muss $1 - a x = 0$ sein $\Rightarrow x = \frac{1}{a}$
Damit ergibt sich folgende Skizze:
Gerade durch Extrema
Aus der Skizze ist ersichtlich, dass die Strecke $| \frac{1}{a} |$ doppelt so lang wie die Strecke $| \frac{1}{2 a} |$ ist.
Mit den Strahlensätzen ist dann auch der y-Achsenabschnitt doppelt so lang wie die Strecke $| \frac{1}{2} e |$ .
Die $y$ -Koordinate dieses gemeinsamen Punktes auf der y-Achse ist dann gleich $e$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Erstelle eine Skizze mit dem Hochpunkt $H P (\frac{1}{2 a} | \frac{1}{2} e)$ und dem Schnittpunkt mit der $x$ -Achse. Berechne dazu $h_{a} (x) = 0 \Rightarrow x_{1} .$
Vergleiche $x_{1}$ mit $\frac{1}{2 a}$ und $\frac{1}{2} e$ mit dem y-Achsenabschnitt der Geraden durch den Hochpunkt und dem Schnittpunkt mit der $x$ -Achse.
Berechnen Sie alle Werte von $a$ , für die der Graph der Ableitungsfunktion $h_{a}^{'}$ vollständig unterhalb oder oberhalb des Graphen der Funktion $h_{a}$ liegt. (5 BE)
Werte von $a$ , für die der Graph der Ableitungsfunktion $h_{a}^{'}$ vollständig unterhalb des Graphen der Funktion $h_{a}$ liegt
Es ist $h_{a} (x) = (1 - a x) \cdot e^{2 \cdot a \cdot x}$ und $h_{a}^{'} (x) = a \cdot (1 - 2 a x) \cdot e^{2 a x}$ .
Berechne $h_{a} (x) = h_{a}^{'} (x)$ :
$(1 - a x) \cdot e^{2 \cdot a \cdot x}$ $=$ $a \cdot (1 - 2 a x) \cdot e^{2 a x}$
$1 - a x$ $=$ $a \cdot (1 - 2 a x)$
↓
Löse die Klammer auf.
$1 - a x$ $=$ $a - 2 a^{2} x$ $+ a x - a$
$1 - a$ $=$ $a x - 2 a^{2} x$
↓
Klammere $a x$ aus.
$1 - a$ $=$ $x a (1 - 2 a)$
Die Gleichung kann nur nach $x$ aufgelöst werden, nur wenn $a (1 - 2 a) \neq 0$ , d.h. $a \neq 0$ und $(1 - 2 a) \neq 0$ .
Man erhält keine Lösung für $a = 0$ und für $1 - 2 a = 0 \Rightarrow a = \frac{1}{2}$ .
Es ist $a = 0 \Rightarrow h_{0} (x) = 1$ und $h_{0}^{'} (x) = 0$ , d.h. $h_{0}^{'} (x)$ liegt ganz unterhalb von $h_{0} (x)$ .
Es ist $a = \frac{1}{2} \Rightarrow$ $h_{\frac{1}{2}} (x) = (1 - \frac{1}{2} x) \cdot e^{2 \cdot \frac{1}{2} \cdot x} = (1 - \frac{1}{2} x) \cdot e^{x} = e^{x} - \frac{1}{2} x e^{x}$ und $h_{\frac{1}{2}}^{'} (x) = \frac{1}{2} \cdot (1 - 2 \frac{1}{2} x) \cdot e^{2 \frac{1}{2} x} = \frac{1}{2} \cdot (1 - x) \cdot e^{x} = \frac{1}{2} e^{x} - \frac{1}{2} x e^{x}$
Damit liegt $h_{\frac{1}{2}}^{'} (x)$ stets unterhalb von $h_{\frac{1}{2}} (x)$ , weil $\frac{1}{2} e^{x}$ stets kleiner als $e^{x}$ ist.
Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.
Sie dient nur der Veranschaulichung.
Graphen der Funktionen h und h'
Dabei ist $h_{\frac{1}{2}}^{'} (x)$ der schwarze Graph und $h_{\frac{1}{2}} (x)$ der orangefarbige Graph.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $h_{a} (x) = h_{a}^{'} (x)$ .
Suche die Werte für $a$ , für die die obige Gleichung keine Lösung hat.

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

$h_{a} (x)$	$=$	$(1 - a \cdot x) \cdot e^{2 \cdot a \cdot x}$
	↓	Setze $x = \frac{1}{2 a}$ ein.
$h_{a} (\frac{1}{2 a})$	$=$	$(1 - a \cdot \frac{1}{2 a}) e^{2 a \cdot \frac{1}{2 a}}$
	↓	Kürze mit $a$ .
	$=$	$(1 - \frac{1}{2}) e^{\frac{2}{2}}$
	↓	Fasse zusammen.
	$=$	$\frac{1}{2} \cdot e^{1}$

$(1 - a x) \cdot e^{2 \cdot a \cdot x}$	$=$	$a \cdot (1 - 2 a x) \cdot e^{2 a x}$
$1 - a x$	$=$	$a \cdot (1 - 2 a x)$
	↓	Löse die Klammer auf.
$1 - a x$	$=$	$a - 2 a^{2} x$	$+ a x - a$
$1 - a$	$=$	$a x - 2 a^{2} x$
	↓	Klammere $a x$ aus.
$1 - a$	$=$	$x a (1 - 2 a)$

Aufgabe 1B

Fünfjahreszeiträume

Hast du eine Frage oder Feedback?

Exponentielle Regression

Logistische Regression

Hast du eine Frage oder Feedback?

Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 kann mit dem folgenden Term bestimmt werden: 1490+∫020g(x)dx

Hast du eine Frage oder Feedback?

Skizze des Koordinatensystems

Hast du eine Frage oder Feedback?

Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005

Hast du eine Frage oder Feedback?

Maximaler Schuldenstand sowie das Jahr, in dem dieser erreicht wird

Hast du eine Frage oder Feedback?

Nachweis für a≠0, dass der maximale Funktionswert unabhängig vom Wert von a ist

Hast du eine Frage oder Feedback?

y-Koordinate dieses gemeinsamen Punktes mithilfe einer Skizze ohne Berechnung der Geradengleichungen

Hast du eine Frage oder Feedback?

Werte von a, für die der Graph der Ableitungsfunktion ha′ vollständig unterhalb des Graphen der Funktion ha liegt

Hast du eine Frage oder Feedback?

Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 kann mit dem folgenden Term bestimmt werden: $1490 + \int_{0}^{20} g (x) d x$

Nachweis für $a \neq 0$ , dass der maximale Funktionswert unabhängig vom Wert von $a$ ist

Werte von $a$ , für die der Graph der Ableitungsfunktion $h_{a}^{'}$ vollständig unterhalb des Graphen der Funktion $h_{a}$ liegt