Teil A: Wahlpflichtteil
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe A 1
Gegeben ist für jede positive reelle Zahl die in definierte Funktion mit . Abbildung 1 zeigt den Graphen von sowie die Tangente an den Graphen von im Punkt .
Abbildung 1
Geben Sie anhand von Abbildung 1 eine Gleichung der Tangente an. (1 P)
Weisen Sie nach, dass für jeden Wert die Tangente an den Graphen von im Punkt die y-Achse im Punkt schneidet. (4 P)
- 2
Aufgabe 2
Betrachtet wird die Schar der in definierten Funktionen mit und . Für jeden Wert von besitzt die Funktion genau eine Extremstelle.
Begründen Sie, dass der Graph von für unterhalb der -Achse verläuft. (2 P)
Die Abbildungen 2 und 3 zeigen jeweils einen Graphen der Schar. Einer der beiden Graphen gehört zu einem positiven Wert von .
Entscheiden Sie, welcher Graph dies ist, und begründen Sie Ihre Entscheidung. (3 P)
- 3
Aufgabe 3
Gegeben ist die Schar der Ebenen mit .
Ermitteln Sie denjenigen Wert von , für den parallel zur Gerade mit der Gleichung und verläuft. (2 P)
Prüfen Sie, ob die Ebene mit der Gleichung zur Schar gehört. (3 P)
- 4
Aufgabe 4
Die Punkte und sind Eckpunkte eines Parallelogramms , dessen Diagonalen sich im Punkt schneiden.
Verschiebt man jeden der Punkte und parallel zur -Achse in die -Ebene, so ergeben sich die Punkte bzw. . Das Viereck ist ein Parallelogramm, dessen Diagonalen sich im Punkt schneiden.
Zeichnen Sie und in Abbildung 4 ein. (3 P)
Abbildung 4
Berechnen Sie den Wert des Skalarprodukts und beurteilen Sie, ob der Winkel zwischen den Vektoren und kleiner ist als . (2 P)
- 5
Aufgabe 5
Abbildung 5 zeigt den Graphen der Dichtefunktion einer normalverteilten Zufallsgröße mit dem Erwartungswert .
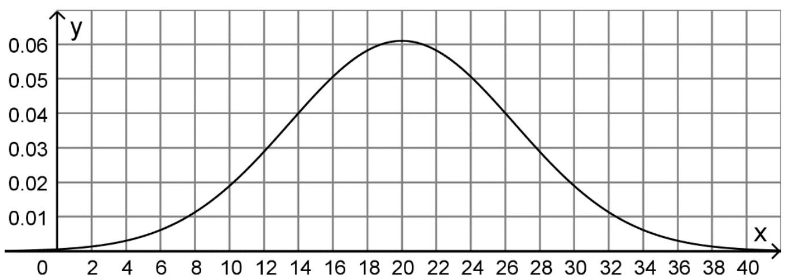
Abbildung 5
Geben Sie die Wahrscheinlichkeit dafür an, dass den Wert annimmt. (1 P)
Gesucht ist die Wahrscheinlichkeit für das Ereignis „ nimmt einen Wert an, der um mehr als von abweicht“.
Erläutern Sie die Überlegungen, die zur folgenden Bestimmung der gesuchten Wahrscheinlichkeit führen:
;
somit gilt: .
(4 P)
- 6
Aufgabe 6
Ein Tetraeder, das mit den Augenzahlen und beschriftet ist, wird zum Würfeln verwendet. Das Tetraeder wurde so manipuliert, dass die Augenzahlen nicht alle mit der gleichen Wahrscheinlichkeit auftreten.
Die Augenzahl tritt mit einer Wahrscheinlichkeit von auf.
Beschreiben Sie in diesem Kontext ein Ereignis, dessen Wahrscheinlichkeit mit dem folgenden Ausdruck berechnet werden kann:
(2 P)
Mit dem Tetraeder wird dreimal gewürfelt. Die Wahrscheinlichkeitsverteilung der Zufallsgröße : „Anzahl der Einsen“ ist in der folgenden Tabelle dargestellt:
k
0
1
2
3
Berechnen Sie den Erwartungswert der Zufallsgröße und die Wahrscheinlichkeit für das Auftreten der Augenzahl . (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?






