Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Aufgaben zu Potenzfunktionen

  1. 1
    123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

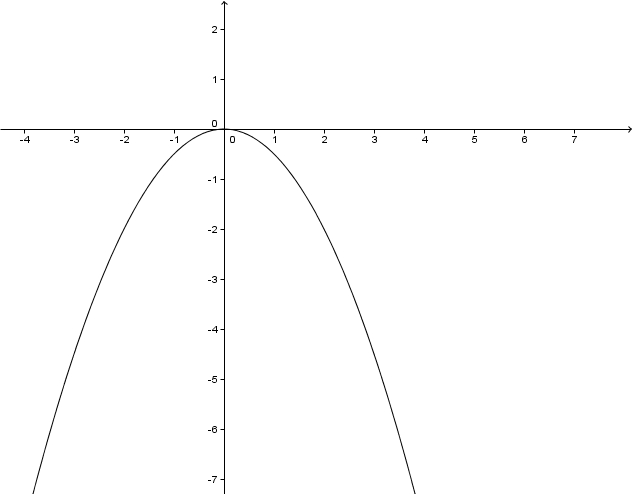
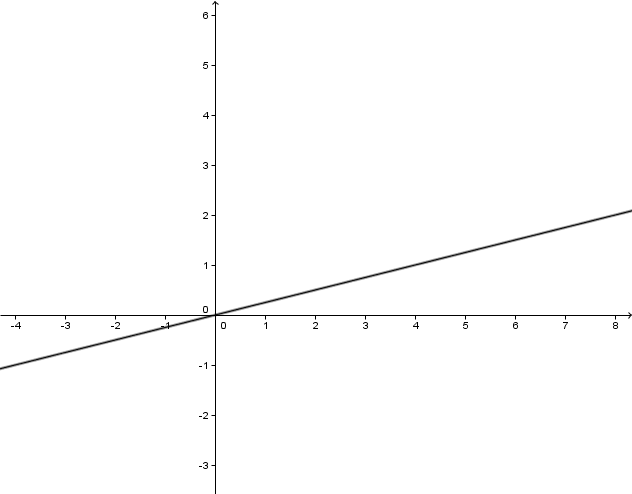
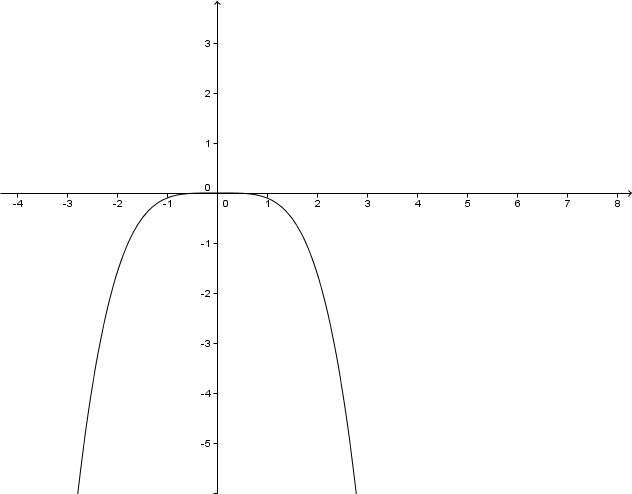
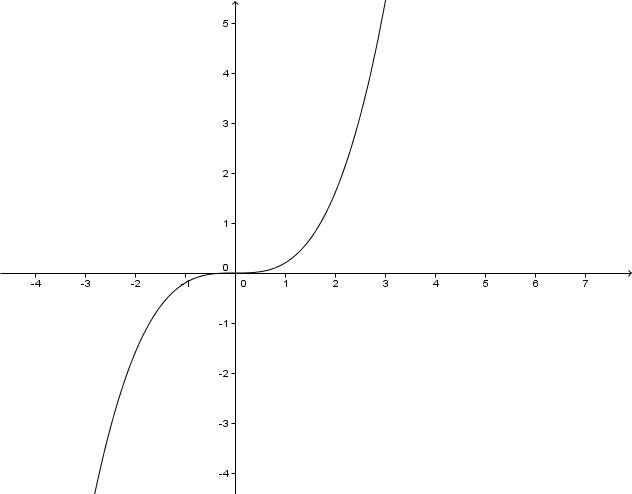
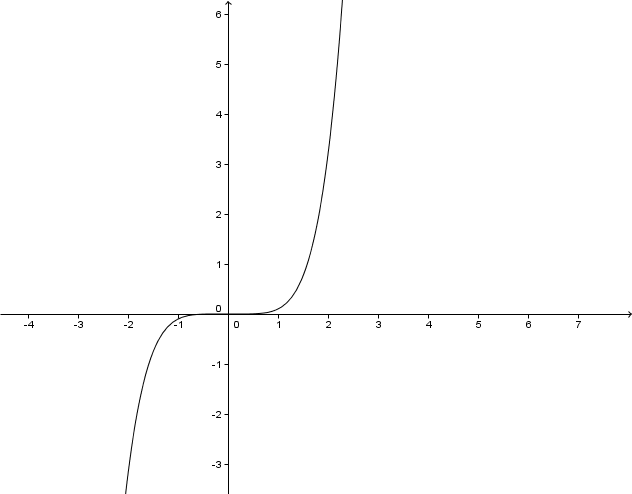
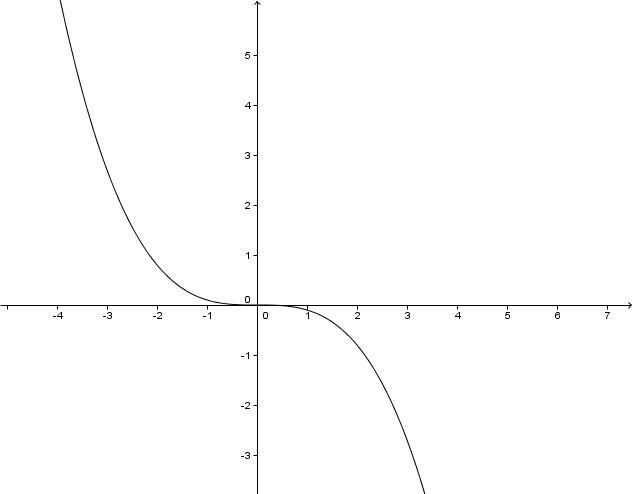
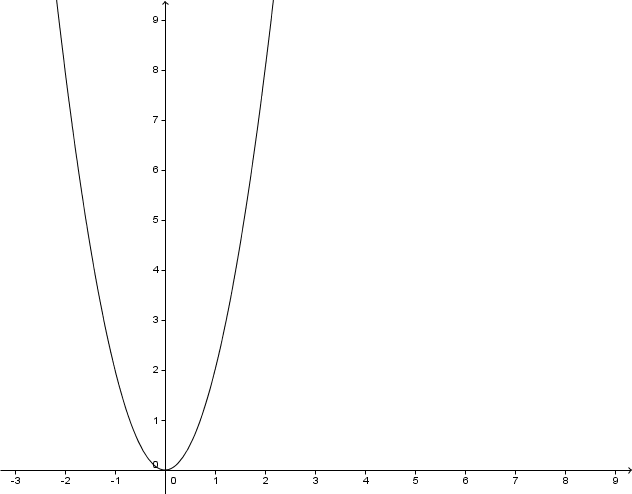
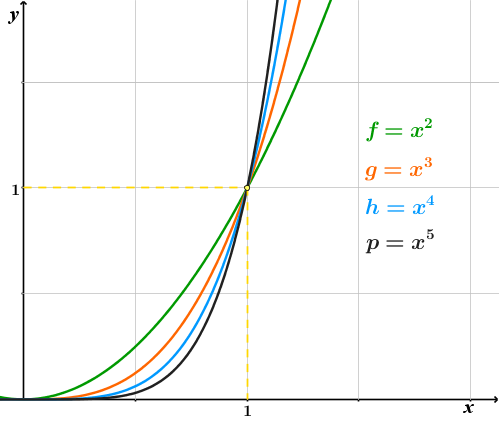
    Betrachte die Graphen der Potenzfunktionen im 11. Quadranten. Für xx- Werte zwischen 00 und 11 liegt der Graph einer Potenzfunktion höheren Grades unterhalb des Graphen einer Potenzfunktion niederen Grades. Für x>1x > 1 ist das genau umgekehrt.

    Begründe dieses Verhalten.

    Plot der Monome zweiten bis fünften Grades
  2. 2
    123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

    Der Graph der Potenzfunktion 3.Grades soll um 2 Einheiten nach links und anschließend um 3 Einheiten nach oben verschoben werden. Gib die Funktionsgleichung für den verschobenen Graphen an.

  3. 3

    Bestimme die Symmetrie und den Verlauf der Graphen folgender Potenzfunktionen und gib jeweils die Wertemenge und den Grad an.

    1. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=4x3f\left(x\right)=4x^3

    2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−160x2f(x)=-160x^2

    3. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−1500xf(x)=-1500x

    4. f(x)=2⋅x6f\left(x\right)=\sqrt2\cdot x^6

    5. f(x)=5f\left(x\right)=5

    6. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−25x5f\left(x\right)=-25x^5

  4. 4

    Bestimme den Grad folgender Potenzfunktionen, mache eine Aussage über das Symmetrieverhalten, den Verlauf des Graphen und die Wertemenge. Zeichne die Graphen jeweils in ein Koordinatensystem.

    1. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−12x2f\left(x\right)=-\frac{1}{2}x^2

    2. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=14xf\left(x\right)=\frac14x

    3. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−110⋅x4f\left(x\right)=-\frac1{10}\cdot x^4

    4. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=15x3f\left(x\right)=\frac15x^3

    5. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=110⋅x5f\left(x\right)=\frac1{10}\cdot x^5

    6. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−12xf\left(x\right)=-\frac12x

    7. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=−110x3f\left(x\right)=-\frac1{10}x^3

    8. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=2x2f\left(x\right)=2x^2

    9. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=15x4f\left(x\right)=\frac15x^4

    10. 123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

      f(x)=25x4f\left(x\right)=\frac25x^4

  5. 5
    123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

    Der Graph der Potenzfunktion vierten Grades soll um 3 Einheiten nach rechts verschoben und anschließend um den Faktor 2 gestreckt werden.

    a. Gib die Funktionsgleichung für den verschobenen Graphen an.

    b. Weise nach, dass der Graph weder zur y-Achse noch zum Ursprung symmetrisch ist.

  6. 6

    Entscheide, ob der Graph der ganzrationalen Funktion ffpunktsymmetrisch bzgl. des Ursprungs oder achsensymmetrisch bzgl. der yy-Achse ist oder ob keine der beiden Symmetrien vorliegt.

    1. f(x)=3f(x)=3

    2. f(x)=15xf(x)=15x

    3. f(x)=4x+1f(x)=4x+1

    4. f(x)=−6x2f(x)=-6x^2

    5. f(x)=6x3−3,5xf(x)=6x^3-3{,}5x

    6. f(x)=−4x4−8f(x)=-4x^4-8

    7. f(x)=6x2+10−7x4f(x)=6x^2+10-7x^4

    8. f(x)=−x5+2x4−3x3+x2f(x)=-x^5+2x^4-3x^3+x^2

    9. f(x)=(2x−3)2f(x)=(2x-3)^2

    10. f(x)=x5(x+3)(x+2)f(x)=x^5(x+3)(x+2)

    11. f(x)=x7−3x5+xf(x)=x^7-3x^5+x

    12. f(x)=−23x5+34xf(x)=-\frac23x^5+\frac34x

    13. f(x)=12x3−12x2−3f(x)=\frac12x^3-\frac12x^2-3

  7. 7
    strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl

    Untersuche die Funktionen auf Achsensymmetrie bezüglich der y-Achse bzw. Punktsymmetrie bezüglich des Ursprungs (Nullpunkt des Koordinatensystems):

    1. f(x)=x11−x5+2xf(x)=x^{11}-x^5+2x

    2. f(x)=x6−9x4f(x)=x^6-9x^4


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?