Aufgaben zu Extremwerten
- 1
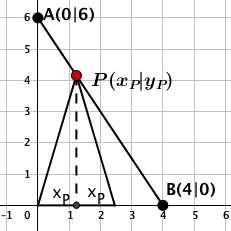
Ein Punkt gleite auf der Strecke mit und .
Er ist die Spitze eines gleichschenkligen Dreiecks mit einer festen Ecke im Koordinatenursprung.
Für welchen Punkt hat das Dreieck den größtmöglichen Flächeninhalt? Wie groß ist dieser?
Im nachfolgenden Applet kannst du - bevor du rechnest - experimentieren.
- 2
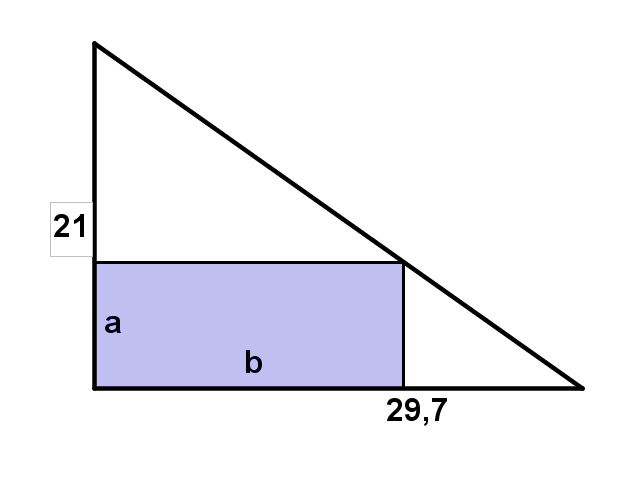
Aus einem diagonal halbierten DIN A4 Blatt soll entsprechend der Zeichnung ein möglichst großflächiges Rechteck geschnitten werden.
Finde die Breite a, für die der Flächeninhalt des Rechtecks maximal ist.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?