Aufgaben zur Definitionsmenge von Bruchtermen und zu Bruchgleichungen

1
Bestimme die Definitionsmenge.
Hinweis zum Eingabefeld: Im Eingabefeld musst du nur die Zahl(en) eingeben, die nicht in der Definitionsmenge enthalten sind. Gib die Zahlen nur durch ein Leerzeichen getrennt ein (also kein Komma oder ähnliches), und ordne sie der Größe nach in aufsteigender Reihenfolge (das heißt, beginne mit der kleinsten).
1. $\displaystyle\frac2x+3=\frac52$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücke
  Finde die Definitionslücken. Setze hierfür den Nenner des Bruchs gleich $0$ .
  $x=0$
  Du kannst erkennen, dass hier der Nenner $0$ wird, wenn $x=0$ ist.
  Schließe die Definitionslücke aus der Definitionsmenge aus.
  $D=\mathbb{Q}\backslash\{0\}$ .
  Die Definitionsmenge ist die Menge der rationalen Zahlen $\mathbb{Q}$ ohne die Zahl $0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\displaystyle\frac{2+x}{x-1}=\frac{3+2x}{x+1}-1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücke
  Finde die Definitionslücken. Setze hierfür die Nenner beider Brüche gleich $0$ .
  $x-1=0\;\;\;\;\Rightarrow\;\;\;\;x=1$
  $x+1=0\;\;\;\;\Rightarrow\;\;\;\;x=-1$
  Du kannst erkennen, dass der Nenner $0$ wird für $x=1$ und $x=-1$ .
  Schließe die Definitionslücke aus der Definitionsmenge aus.
  $D=\mathbb{Q}\backslash\{-1, 1\}$ .
  Die Definitionsmenge ist die Menge der rationalen Zahlen $\mathbb{Q}$ ohne die Zahl $-1$ und die Zahl $1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\displaystyle\frac{1}{x-3}=\frac{2}{x^2-2x}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionslücke
  Definitionsmenge
  Für diese Aufgabe musst du wissen, was eine Definitionslücke ist und wie du die Definitionsmenge einer Bruchgleichung bestimmst.
  Finde die Definitionslücken. Setzte den Nenner beider Brüche gleich $0$ .
  1. Bruch:
  $x-3=0\;\;\;\;\Rightarrow\;\;\;\;x=3$
  2. Bruch:
  Hier brauchst du einen Trick! Klammere aus und prüfe, wann einer der beiden Faktoren gleich $0$ wird.
  $x^2-2x=0$
  Klammere $x$ aus.
  $x\cdot(x-2)=0$
  Du musst jetzt prüfen, wann einer der beiden Faktoren $0$ wird. Setze sie jeweils gleich $0$ .
  $x=0$
  $x-2=0\;\;\;\;\Rightarrow\;\;\;\;x=2$
  Du kannst erkennen, dass der Nenner des zweiten Bruchterms $0$ wird für $x=0$ und $x=2$ und der erste Bruchterm $0$ wird für $x=3$ .
  Schließe die Definitionslücken aus der Definitionsmenge aus.
  $D=\mathbb{Q}\backslash\{0, 2, 3\}$ .
  Die Definitionsmenge ist die Menge der rationalen Zahlen $\mathbb{Q}$ ohne die Zahlen $0$ , $2$ und $3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Löse folgende Bruchgleichung $\displaystyle\frac{1570}{x}=4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Definitionsmenge bestimmen
Der Nenner darf nie 0 werden! Daher muss $x=0$ ausgeschlossen werden.
$D=\mathbb{Q} \backslash \{0\}$
Bruchgleichung lösen
Bei dieser Aufgabe musst du nur das $x$ auf die andere Seite bringen. Da $x$ im Nenner steht, musst du mit $x$ multiplizieren
$\frac{1570}{x}=4$
Mit $x$ multiplizieren.
$1570=4\cdot x$
Durch 4 dividieren.
$x=\frac{1570}{4}=392{,}5$
Da $392{,}5$ in der Definitionsmenge liegt, ist dies die Lösung der Bruchgleichung.

Beim Lösen einer Gleichung der Form $\displaystyle\frac ab=\frac cd$ muss man „Über-Kreuz-Multiplizieren“. Das heißt $\displaystyle\frac ab=\frac cd$ ist das Gleiche wie $\displaystyle a\cdot d=b\cdot c$ .

Wende dieses Vorgehen bei den folgenden Bruchgleichungen an.

$\displaystyle\frac3{2x+1}=\frac2{2-x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren

Definitionsmenge bestimmen

Zunächst musst du die Definitionsmenge der Gleichung bestimmen.

$\dfrac{3}{2x+1}=\dfrac{2}{2-x}$

Keiner der beiden Nenner darf $0$ werden.

Deshalb musst du aus der Definitionsmenge alle Zahlen ausschließen, für die $0$ in einem der Nenner ergeben würde.

Verboten sind hier also:

$2x+1=0$
$2-x=0$

Erste Gleichung lösen!

$\displaystyle 2x+1$	$=$	$\displaystyle 0$	$\displaystyle -1$
$\displaystyle 2x$	$=$	$\displaystyle -1$	$\displaystyle :2$
$\displaystyle x$	$=$	$\displaystyle -\frac{1}{2}$

Zweite Gleichung lösen!

$\displaystyle 2-x$	$=$	$\displaystyle 0$	$\displaystyle -2$
$\displaystyle -x$	$=$	$\displaystyle -2$	$\displaystyle :\left(-1\right)$
$\displaystyle x$	$=$	$\displaystyle 2$

Daher müssen die Zahlen $-\dfrac{1}{2}$ und $2$ aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.

Die Definitionsmenge ist $D =\mathbb {Q}\backslash\left\{-0{,}5;\ 2\right\}$ , wenn als Grundmenge die Menge $\mathbb{Q}$ der rationalen Zahlen verwendet wird.

Bruchgleichung lösen

Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:

$\dfrac{3}{2x+1}=\dfrac{2}{2-x}\quad$

Über-Kreuz-Multiplizieren! $\dfrac ab=\dfrac cd \Leftrightarrow a\cdot d=c\cdot b$

$\displaystyle \frac{3}{2x+1}$	$=$	$\displaystyle \frac{2}{2-x}$	$\displaystyle \cdot\left(2x+1\right)\left(2-x\right)$
$\displaystyle 3\cdot\left(2-x\right)$	$=$	$\displaystyle 2\cdot\left(2x+1\right)$
	↓	Multipliziere die Klammern aus.
$\displaystyle 6-3x$	$=$	$\displaystyle 4x+2$	$\displaystyle -2+3x$
	↓	Löse dann die Gleichung durch Umformen nach $x$ auf.
$\displaystyle 4$	$=$	$\displaystyle 7x$	$\displaystyle :7$
$\displaystyle \frac{4}{7}$	$=$	$\displaystyle x$

Überprüfe jetzt noch, ob $x=\frac{4}{7}$ in der Definitionsmenge enthalten ist. Es gilt $x=\dfrac{4}{7} \in D$ , also ist die Lösungsmenge $\mathbb L= \left\{ \dfrac{4}{7}\right\}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$\displaystyle\frac{x-2}{3+x}=\frac{2x}{2x-3}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren

Definitionsbereich bestimmen

Zunächst musst du die Definitionsmenge der Gleichung bestimmen.

$\displaystyle\frac{x-2}{3+x}=\frac{2x}{2x-3}$

Keiner der beiden Nenner darf $0$ werden.

Aus der Definitionsmenge musst du deshalb alle Zahlen ausschließen, für die einer der Nenner $0$ ergeben würde.

Verboten sind hier also:

$3+x=0$
$2x-3=0$

Löse die erste Gleichung!

$\displaystyle 3+x$	$=$	$\displaystyle 0$	$\displaystyle -3$
$\displaystyle x$	$=$	$\displaystyle -3$

Löse die zweite Gleichung!

$\displaystyle 2x-3$	$=$	$\displaystyle 0$	$\displaystyle +3$
$\displaystyle 2x$	$=$	$\displaystyle 3$	$\displaystyle :2$
$\displaystyle x$	$=$	$\displaystyle \frac{3}{2}$

Daher müssen die Zahlen $-3$ und $\dfrac{3}{2}$ aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.

Die Definitionsmenge ist $D =\mathbb {Q}\backslash\left\{-3,\dfrac{3}{2}\right\}$ , wenn als Grundmenge die Menge $\mathbb{Q}$ der rationalen Zahlen verwendet wird.

Bruchgleichung lösen

Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:

$\displaystyle \frac{x-2}{3+x}$	$=$	$\displaystyle \frac{2x}{2x-3}$	$\displaystyle \cdot\left(3+x\right)\left(2x-3\right)$
$\displaystyle \left(x-2\right)\cdot\left(2x-3\right)$	$=$	$\displaystyle 2x\cdot\left(3+x\right)$
	↓	Klammern ausmultiplizieren.
$\displaystyle 2x^2-3x-4x+6$	$=$	$\displaystyle 6x+2x^2$
	↓	Löse nun die Gleichung nach $x$ auf!
$\displaystyle 2x^2-7x+6$	$=$	$\displaystyle 6x+2x^2$	$\displaystyle -2x^2+7x$
$\displaystyle 6$	$=$	$\displaystyle 13x$	$\displaystyle :13$
$\displaystyle \frac{6}{13}$	$=$	$\displaystyle x$

Überprüfe jetzt noch, ob $x=\dfrac{6}{13}$ in der Definitionsmenge enthalten ist. $x=\dfrac{6}{13} \in D$ also ist die Lösungsmenge $\mathbb L= \left\{ \dfrac{6}{13}\right\}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$\displaystyle 1+\frac2{2x-1}=\frac x{x+2}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Über-Kreuz-Multiplizieren

Definitionsbereich bestimmen

Zunächst musst du die Definitionsmenge der Gleichung bestimmen.

$\displaystyle1+\frac2{2x-1}=\frac x{x+2}$

Keiner der beiden Nenner darf $0$ werden.

Aus der Definitionsmenge musst du deshalb alle Zahlen ausschließen, für die einer der Nenner $0$ ergeben würde.

Verboten ist hier:

$2x-1=0$
$x+2=0$

Löse die erste Gleichung.

$\displaystyle 2x-1$	$=$	$\displaystyle 0$	$\displaystyle +1$
$\displaystyle 2x$	$=$	$\displaystyle 1$	$\displaystyle :2$
$\displaystyle x$	$=$	$\displaystyle \frac{1}{2}$

Löse die zweite Gleichung.

$\displaystyle x+2$	$=$	$\displaystyle 0$	$\displaystyle -2$
$\displaystyle x$	$=$	$\displaystyle -2$

Daher müssen die Zahlen $-2$ und $\dfrac{1}{2}$ aus der Definitionsmenge der Bruchgleichung ausgeschlossen werden.

Die Definitionsmenge ist $D =\mathbb {Q}\backslash\left\{-2,\dfrac{1}{2}\right\}$ , wenn als Grundmenge die Menge $\mathbb{Q}$ der rationalen Zahlen verwendet wird.

Bruchgleichung lösen

Nun löst du die Bruchgleichung mit der Methode des Über-Kreuz-Multiplizierens:

Zunächst musst du die linke Seite der Gleichung auf einen gemeinsamen Bruch bringen.

$\displaystyle 1+\frac{2}{2x-1}$	$=$	$\displaystyle \frac{x}{x+2}$
	↓	Den Summanden $1$ mit $2x-1$ erweitern.
$\displaystyle \frac{2x-1}{2x-1}+\frac{2}{2x-1}$	$=$	$\displaystyle \frac{x}{x+2}$
	↓	Brüche auf der linken Seite addieren.
$\displaystyle \frac{2x-1+2}{2x-1}$	$=$	$\displaystyle \frac{x}{x+2}$
	↓	Auf der linken Seite den Zähler zusammenfassen.
$\displaystyle \frac{2x+1}{2x-1}$	$=$	$\displaystyle \frac{x}{x+2}$	$\displaystyle \cdot\left(2x-1\right)\left(x+2\right)$
	↓	Nun wendest du die Methode des Über-Kreuz-Multiplizierens an.
$\displaystyle (2x+1)\cdot(x+2)$	$=$	$\displaystyle x\cdot(2x-1)$
	↓	Klammern ausmultiplizieren
$\displaystyle 2x^2+4x+x+2$	$=$	$\displaystyle 2x^2-x$
	↓	Linke Seite zusammenfassen.
$\displaystyle 2x^2+5x+2$	$=$	$\displaystyle 2x^2-x$	$\displaystyle -2x^2+x$
	↓	Löse nach $x$ auf.
$\displaystyle 6x+2$	$=$	$\displaystyle 0$	$\displaystyle -2$
$\displaystyle 6x$	$=$	$\displaystyle -2$	$\displaystyle :6$
$\displaystyle x$	$=$	$\displaystyle -\frac{2}{6}$
	↓	Kürzen.
$\displaystyle x$	$=$	$\displaystyle -\frac{1}{3}$

Überprüfe jetzt noch, ob $x=-\dfrac{1}{3}$ in der Definitionsmenge enthalten ist. Wegen $x=-\dfrac{1}{3} \in D$ ist die Lösungsmenge $\mathbb L= \left\{ -\dfrac{1}{3}\right\}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Löse die Bruchgleichung:

\displaystyle \frac{2+x}{1-x}=\frac{3x}{2-3x}

5
Handelt es sich um eine Bruchgleichung?
1. $\displaystyle\frac2{x+3}+3=15$
  Ja, es ist eine Bruchgleichung.
  Nein, es ist keine Bruchgleichung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
  Eigenschaft $1$
  Durch bloßes Betrachten kannst du erkennen, dass in der Angabe eine Gleichung steht. Das Merkmal dafür ist das " $=$ ".
  Eigenschaft $2$ und $3$
  Zudem ist ein Bruch enthalten, nämlich $\displaystyle\frac2{x+3}$ und dieser hat eine Variable im Nenner.
  Somit sind alle Bedingungen für eine Bruchgleichung vorhanden.
  Die Antwort lautet: Ja, es ist eine Bruchgleichung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\displaystyle\frac{25x}{x^2-4}+35$
  Nein, es ist keine Bruchgleichung.
  Ja, es ist eine Bruchgleichung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
  Eigenschaft $1$
  Hier kannst du erkennen, dass keine Gleichung vorliegt, da kein " $=$ " vorhanden ist.
  Folglich musst du die anderen Merkmale garnicht mehr prüfen.
  Die Antwort lautet: Nein, es ist keine Bruchgleichung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\displaystyle\frac x{4x-5}=\frac{x^2}{7x-4}+3$
  Ja, es ist eine Bruchgleichung.
  Nein, es ist keine Bruchgleichung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
  Eigenschaft $1$
  Durch bloßes Betrachten kannst du erkennen, dass in der Angabe eine Gleichung steht. Das Merkmal dafür ist das " $=$ ".
  Eigenschaft $2$ und $3$
  Zudem sind die Brüche $\displaystyle\frac{x}{4x-5}$ und $\displaystyle\frac{x^2}{7x-4}$ enthalten, welche eine Variable $x$ im Nenner haben.
  Somit sind alle Bedingungen für eine Bruchgleichung vorhanden.
  Die Antwort lautet: Ja, es ist eine Bruchgleichung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $\displaystyle\frac{2x^2-x}4=\frac{5x-3}{34}$
  Nein, es ist keine Bruchgleichung.
  Ja, es ist eine Bruchgleichung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
  Eigenschaft $1$
  Durch bloßes Hinsehen kannst du erkennen, dass eine Gleichung vorliegt.
  Eigenschaft $2$
  Zudem sind die Brüche $\displaystyle\frac{2x^2-x}{4}$ und $\displaystyle\frac{5x-3}{34}$ vorhanden.
  Eigenschaft $3$
  Vorsicht! Keiner der Brüche hat eine Variable im Nenner.
  Eine der Eigenschaften ist nicht erfüllt und somit handelt es sich nicht um eine Bruchgleichung.
  Die Antwort lautet: Nein, es ist keine Bruchgleichung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $\displaystyle31+\frac{2x-1}{x^3+2}=\frac2x$
  Ja, es ist eine Bruchgleichung.
  Nein, es ist keine Bruchgleichung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen
  Eigenschaft $1$
  Durch bloßes Betrachten kannst du erkennen, dass in der Angabe eine Gleichung steht. Das Merkmal dafür ist das " $=$ ".
  Eigenschaft $2$ und $3$
  Zudem sind Brüche, nämlich $\displaystyle\frac2x$ und $\displaystyle\frac{2x-1}{x^3+2}$ , vorhanden. Diese haben ebenfalls eine Variable im Nenner.
  Somit sind alle Bedingungen für eine Bruchgleichung vorhanden.
  Die Antwort lautet: Ja, es ist eine Bruchgleichung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
Bestimme die Lösungsmenge der Bruchgleichung mit Hilfe der Grafik!
1. $\dfrac5{x+1}=-\dfrac{15}{x-3}$
  $\mathbb L=\{0\}$
  $\mathbb L=\{5\}$
  $\mathbb L=\{0;5\}$
  $\mathbb L=\emptyset$
  
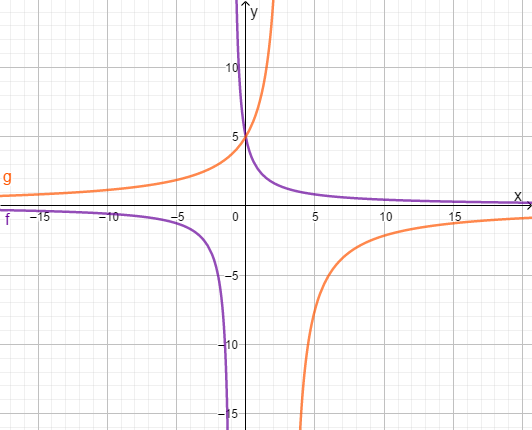
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen ablesen
  Die Lösung der Gleichung ist die $x$ -Koordinate des Schnittpunkts!Die zwei Graphen haben genau einen gemeinsamen Schnittpunkt also gibt es genau eine Lösung! Dieser Schnittpunkt liegt bei $(0\ |\ 5)$ . Also ist die Lösungsmenge $\mathbb L=\{0\}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Lösungsmenge besteht aus den $x$ -Koordinaten aller Schnittpunkte
2. $\dfrac{4x}{x^2-1}=1+\dfrac{1}{x^2-1}$
  $\mathbb L=\{0;4\}$
  $\mathbb L=\{1; 4\}$
  $\mathbb L=\{0\}$
  $\mathbb L=\{4\}$
  
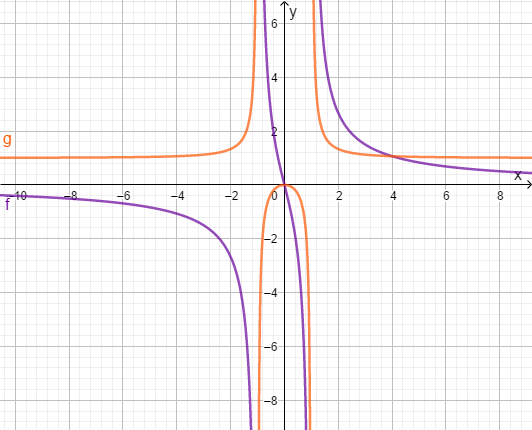
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen ablesen
  Die Lösungsmenge besteht aus den $x$ -Koordinaten der Schnittpunkte der Graphen. Hier gibt es genau zwei Schnittpunkte, nämlich $(0\ | \ 0)$ und $\left(4\ |\ \dfrac {16}{15}\right)$ . Also besteht die Lösungsmenge $\mathbb L=\{0{,}4\}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Lösungsmenge besteht aus den $x$ -Koordinaten der Schnittpunkte!

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \dfrac{2+x}{\textcolor{red}{1-x}}$	$=$	$\displaystyle \dfrac{3x}{\textcolor{blue}{2-3x}}$	$\displaystyle \cdot (1-x) \cdot (2-3x)$
$\displaystyle (2+x)\cdot \textcolor{blue}{(2-3x)}$	$=$	$\displaystyle \textcolor{blue}{3x}\cdot \textcolor{red}{(1-x)}$
	↓	Ausmultiplizieren.
$\displaystyle 4-6x+2x-3x^2$	$=$	$\displaystyle 3x-3x^2$
$\displaystyle 4-4x-3x^2$	$=$	$\displaystyle 3x-3x^2$	$\displaystyle +3x^2$
$\displaystyle 4-4x$	$=$	$\displaystyle 3x$	$\displaystyle +4x$
$\displaystyle 4$	$=$	$\displaystyle 7x$	$\displaystyle :7$
$\displaystyle x$	$=$	$\displaystyle \frac{4}{7}$