Aufgaben zur Parallelverschiebung
- 1
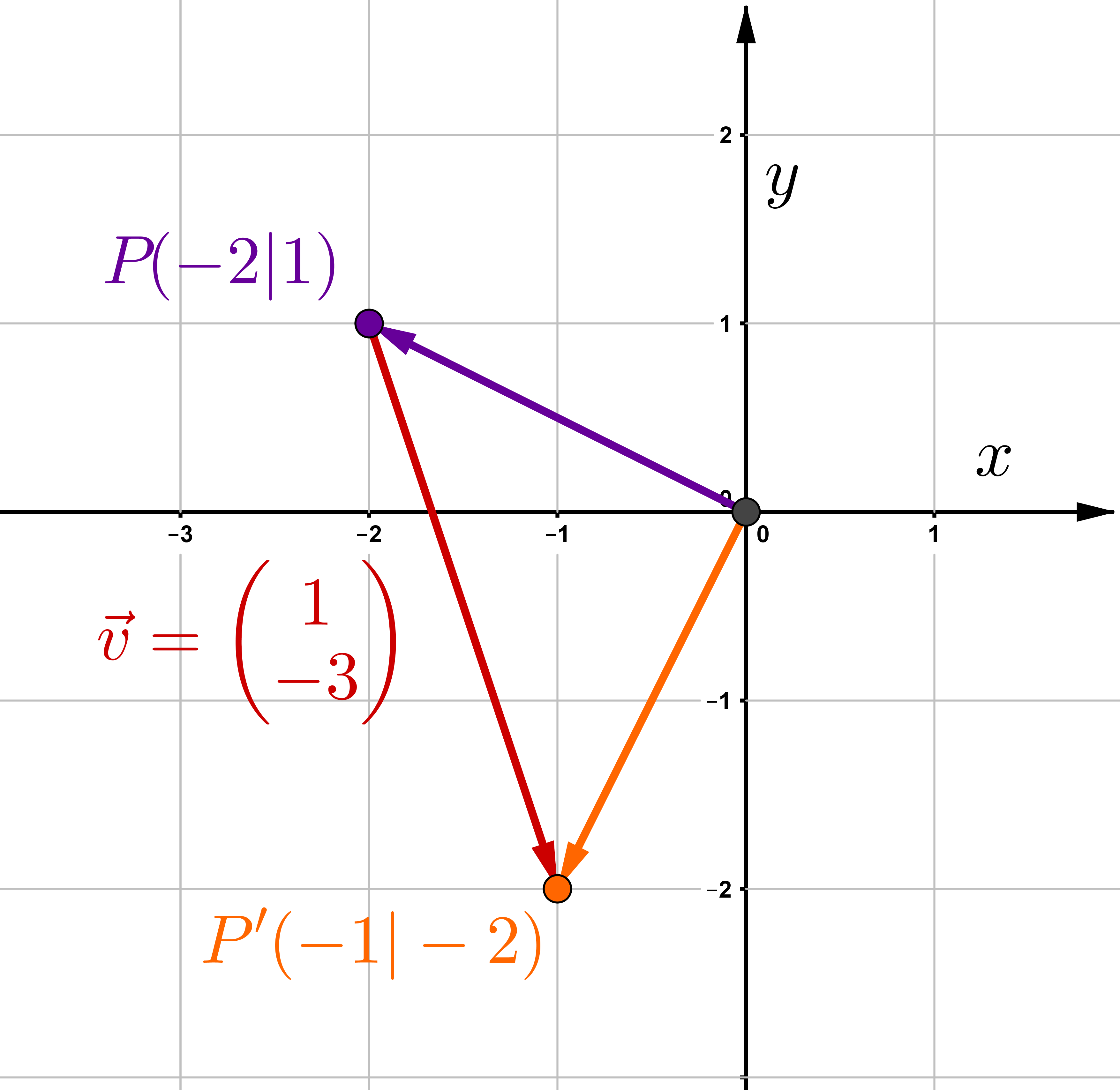
Verschiebe den Punkt um den Vektor . Gib die Koordinaten von an.
Gib den Punkt jeweils in das Eingabefeld ein, zum Beispiel:
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung eines Punktes
1. Variante: Lösung mit der Koordinatenform
2. Variante: Lösung mit der Matrixform
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung eines Punktes
1. Variante: Lösung mit der Koordinatenform
Addiere den Vektor zu dem Ortsvektor
2. Variante: Lösung mit der Matrixform
Führe die Matrix-Vektor-Multiplikation durch
Hast du eine Frage oder Feedback?
- 2
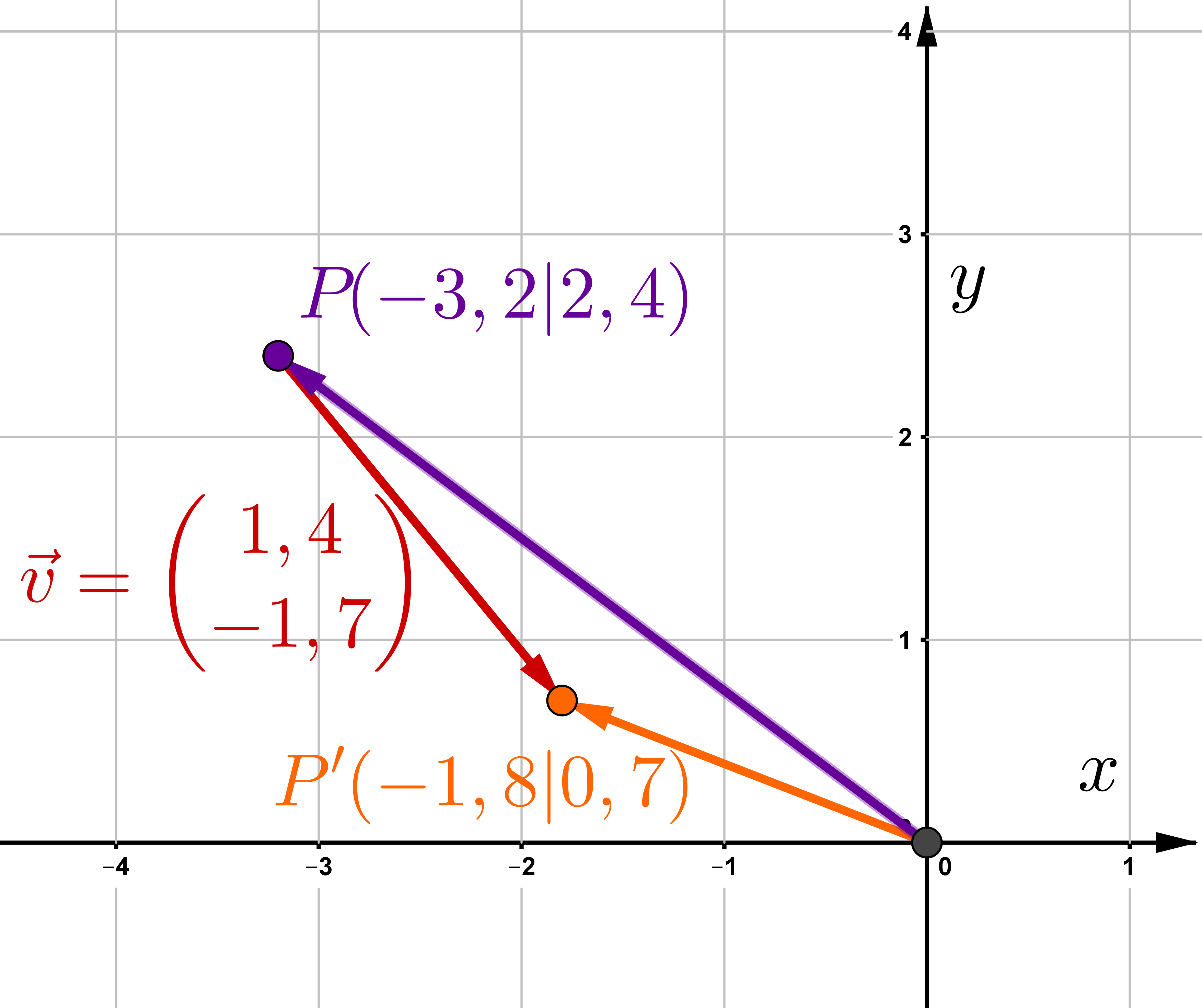
Um welchen Vektor wurde auf verschoben?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung eines Punktes
1. Variante: Lösung mit der Koordinatenform
2. Variante: Lösung mit der Matrixform
↓ ↓ Führe die Matrix-Vektor- Multiplikation durch
↓ Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung eines Punktes
1. Variante: Lösung mit der Koordinatenform
2. Variante: Lösung mit der Matrixform
↓ ↓ Führe die Matrix-Vektor-Multiplikation durch
↓ Hast du eine Frage oder Feedback?
- 3
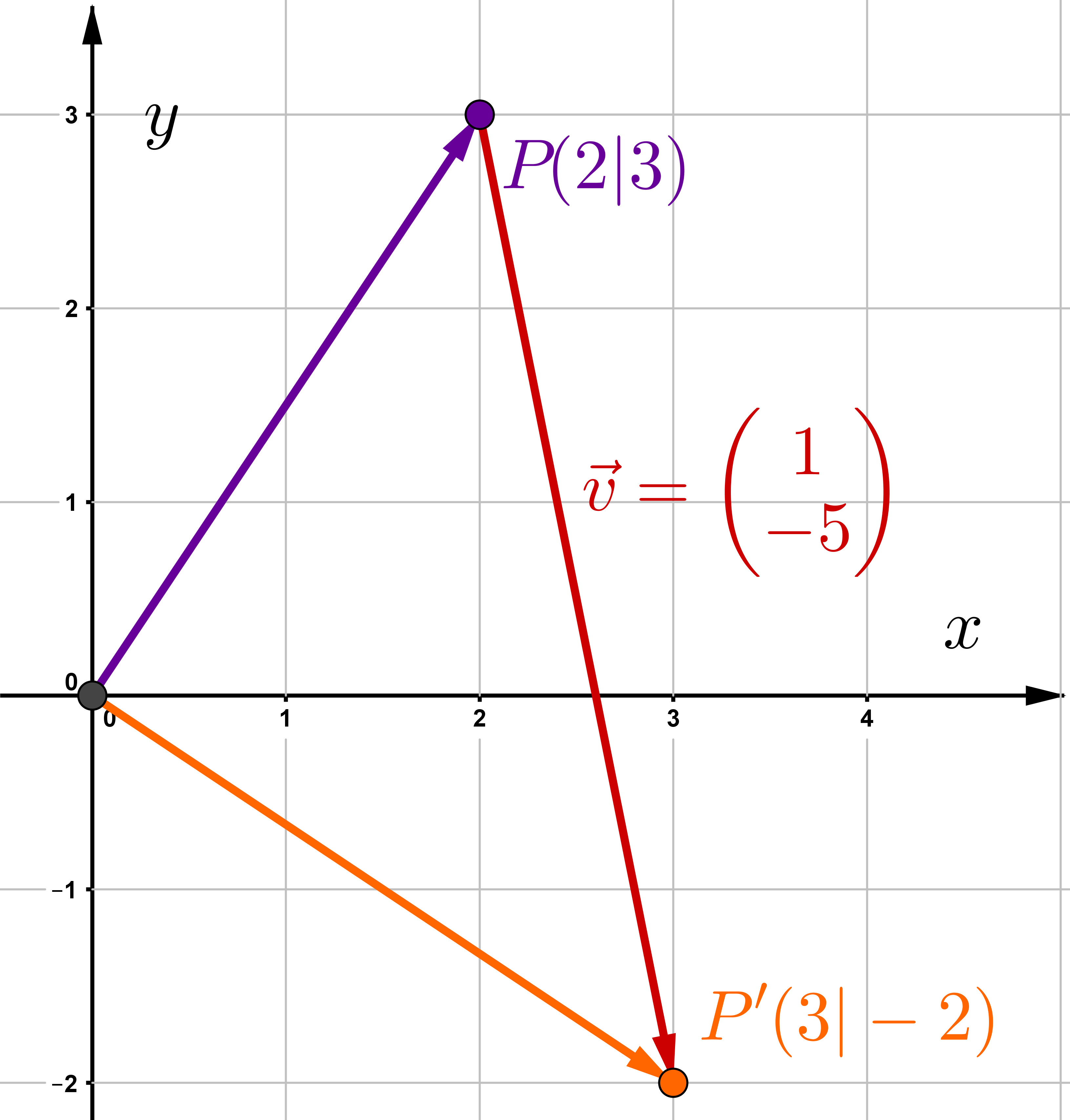
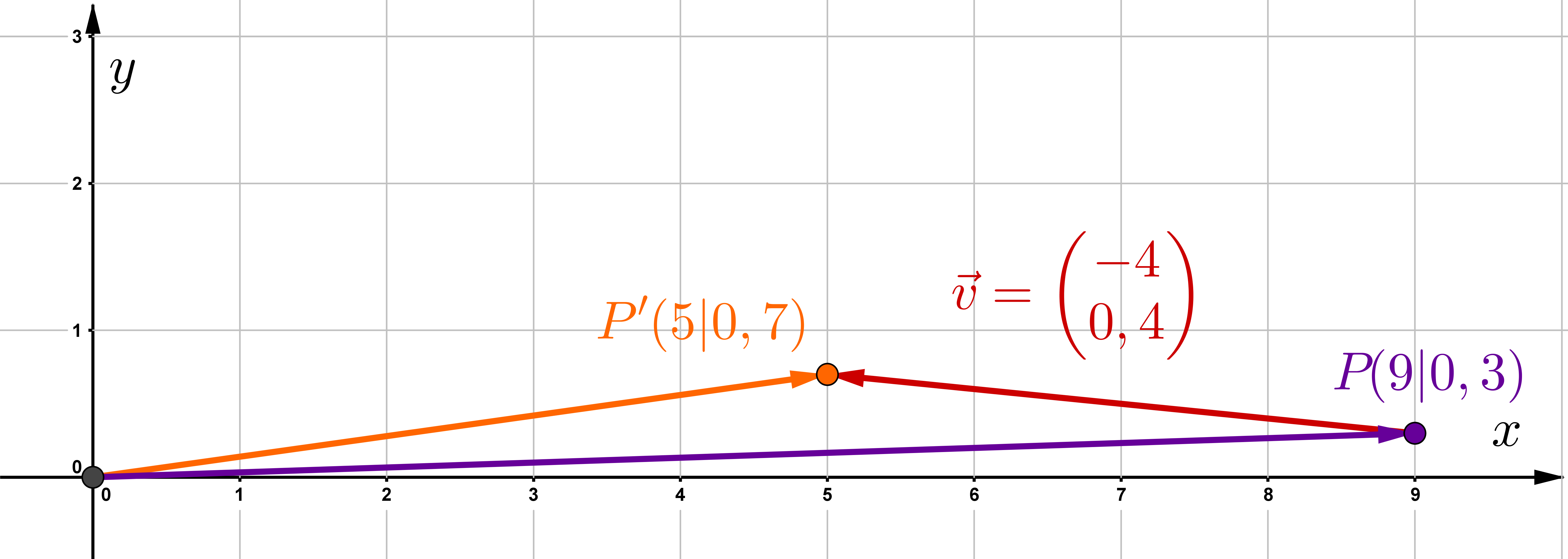
Welcher Punkt wurde um den Vektor auf verschoben?
Gib den Punkt jeweils in das Eingabefeld ein, zum Beispiel:
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung eines Punktes
1. Variante: Lösung mit der Koordinatenform
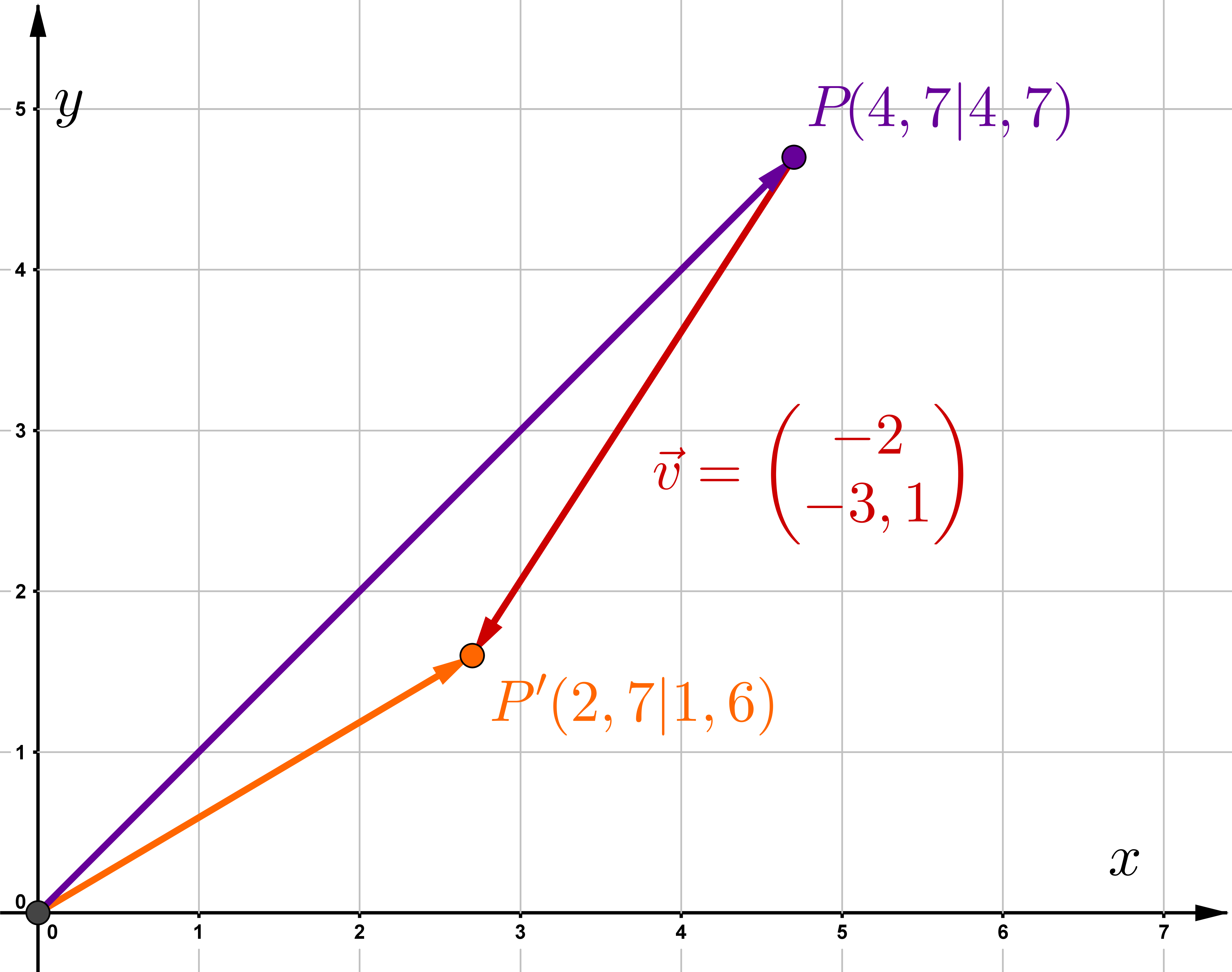
2. Variante: Lösung mit der Matrixform
↓ Führe die Matrix-Vektor-Multiplikation durch
↓ ↓ Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung eines Punktes
1. Variante: Lösung mit der Koordinatenform
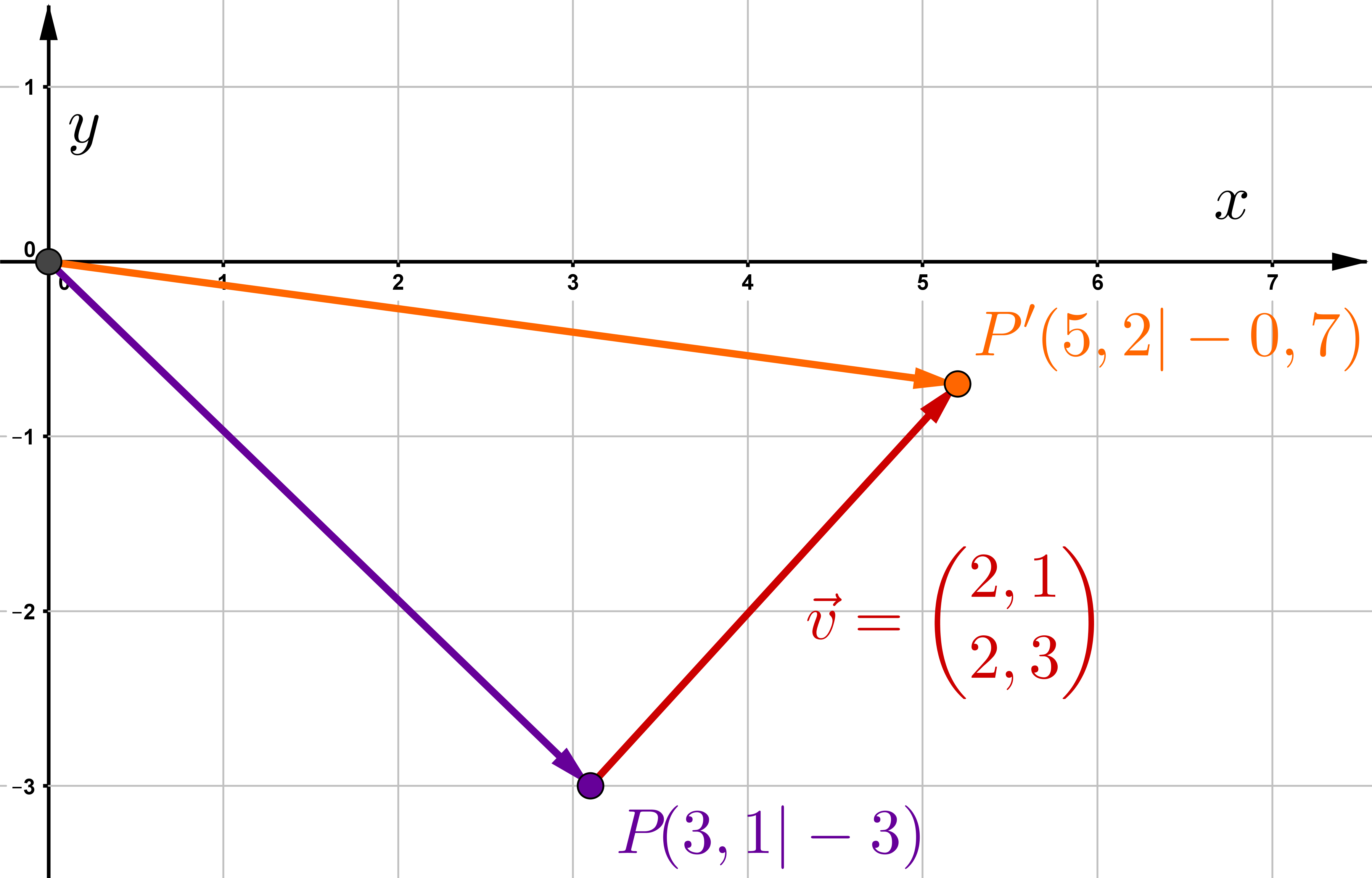
2. Variante: Lösung mit der Matrixform
↓ Führe die Matrix-Vektor-Multiplikation durch
↓ ↓ Hast du eine Frage oder Feedback?
- 4
Verschiebe die Gerade um den Vektor .
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung einer Gerade
↓ Setze die Geradengleichung in die Matrixform ein.
↓ Damit erhältst du zwei Gleichungen in Abhängigkeit von .
Löse die erste Gleichung nach x auf und setze sie in die zweite Gleichung ein:
Somit hast du die neue Geradengleichung in Abhängigkeit von .
Alternativlösung
Wähle zwei Punkte, die auf der Gerade liegen, z.B. den x- und y-Achsenabschnitt.
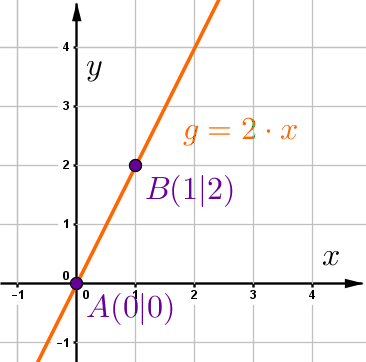
und
Verschiebe die Punkte und um den Vektor .
1. Variante: Berechnung in Koordinatenform
Addiere den Vektor zu den Ortsvektoren und
Setze die Koordinaten der Punkte ein.
2. Variante: Berechnung in Matrixform
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ ↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ und
Berechne die Steigung durch den Differenzenquotienten.
Setze und den Punkt in die Geradengleichung ein und stelle sie um, um zu bestimmen.
Stelle die Geradengleichung auf.
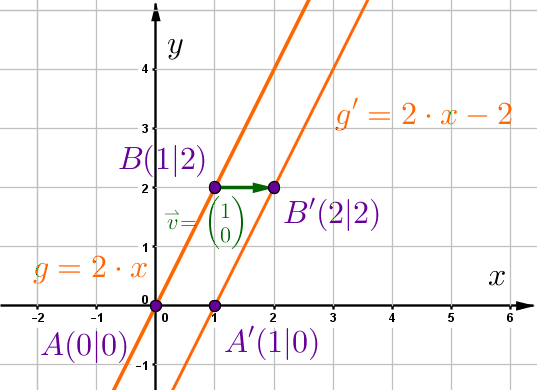
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung einer Gerade
,
↓ Setze die Geradengleichung in die Matrixform ein.
↓ Damit erhältst du zwei Gleichungen in Abhängigkeit von x.
Löse die erste Gleichung nach x auf und setze sie in die zweite Gleichung ein.
Somit hast du die neue Geradengleichung in Abhängigkeit von
Alternativlösung:
Wähle zwei Punkte, die auf der Gerade liegen, z.B. den x- und y-Achsenabschnitt. In diesem Fall betrachtest du den y-Abschnitt und gehst dann nach unten und nach links, sodass du bei landest.
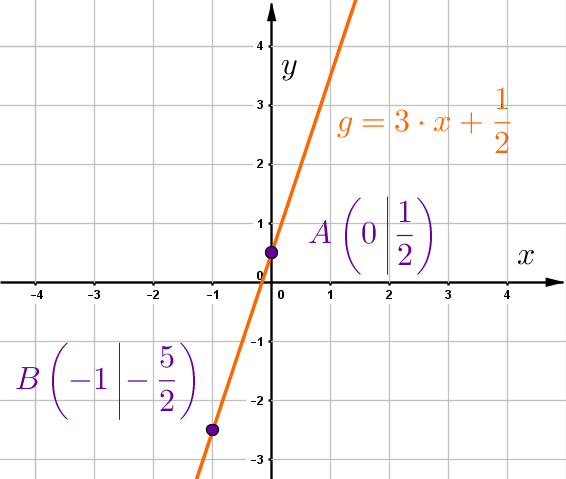
und
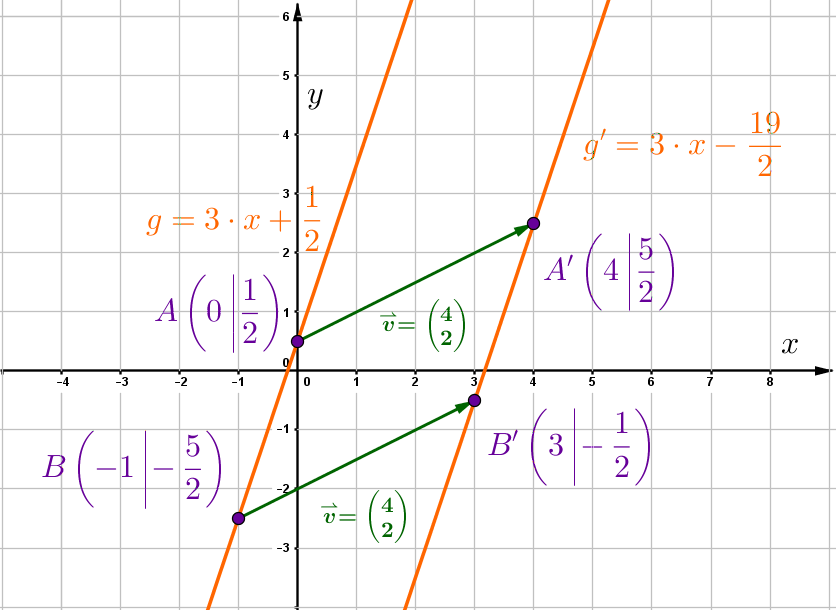
Verschiebe die Punkte und um den Vektor
1. Variante: Berechnung in Koordinatenform
Addiere den Vektor zu den Ortsvektoren und
Setze die Koordinaten der Punkte ein.
2. Variante: Berechnung in Matrixform
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ ↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ und
Berechne die Steigung durch den Differenzenquotienten.
Setze und den Punkt in die Geradengleichung ein und stelle sie um, um zu bestimmen.
Stelle die Geradengleichung auf.
Hast du eine Frage oder Feedback?
- 5
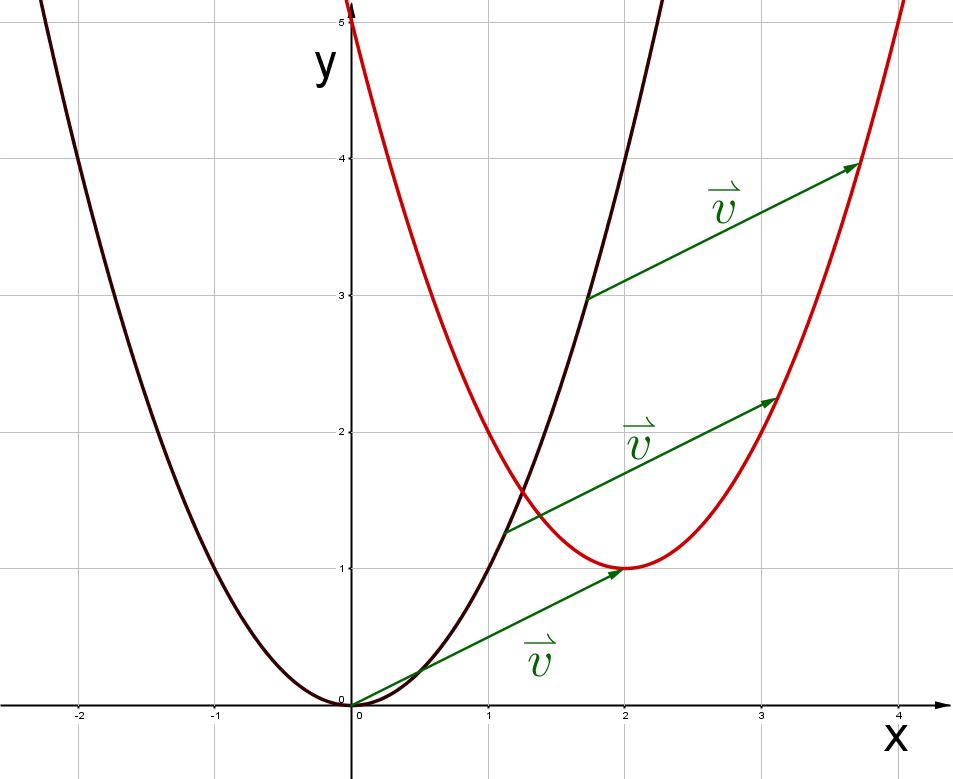
Verschiebe die Funktion um den Vektor .
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funktion eine Parallelverschiebung um den Vektor durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funtion eine Parallelverschiebung um einen Vektor zu durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Setze die Gleichung für in die Gleichung für ein und vereinfache.
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Setze die Gleichung für in die Gleichung für ein.
Dies ist die Funktionsgleichung der verschobenen Funktion.
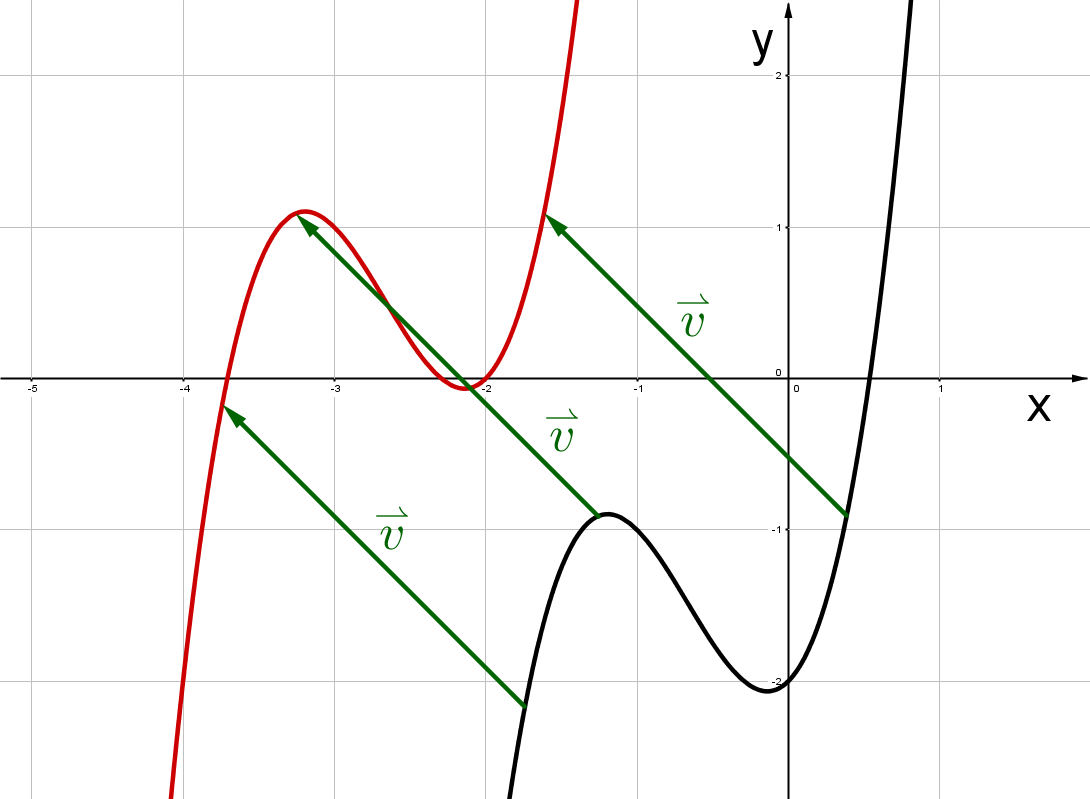
Hast du eine Frage oder Feedback?
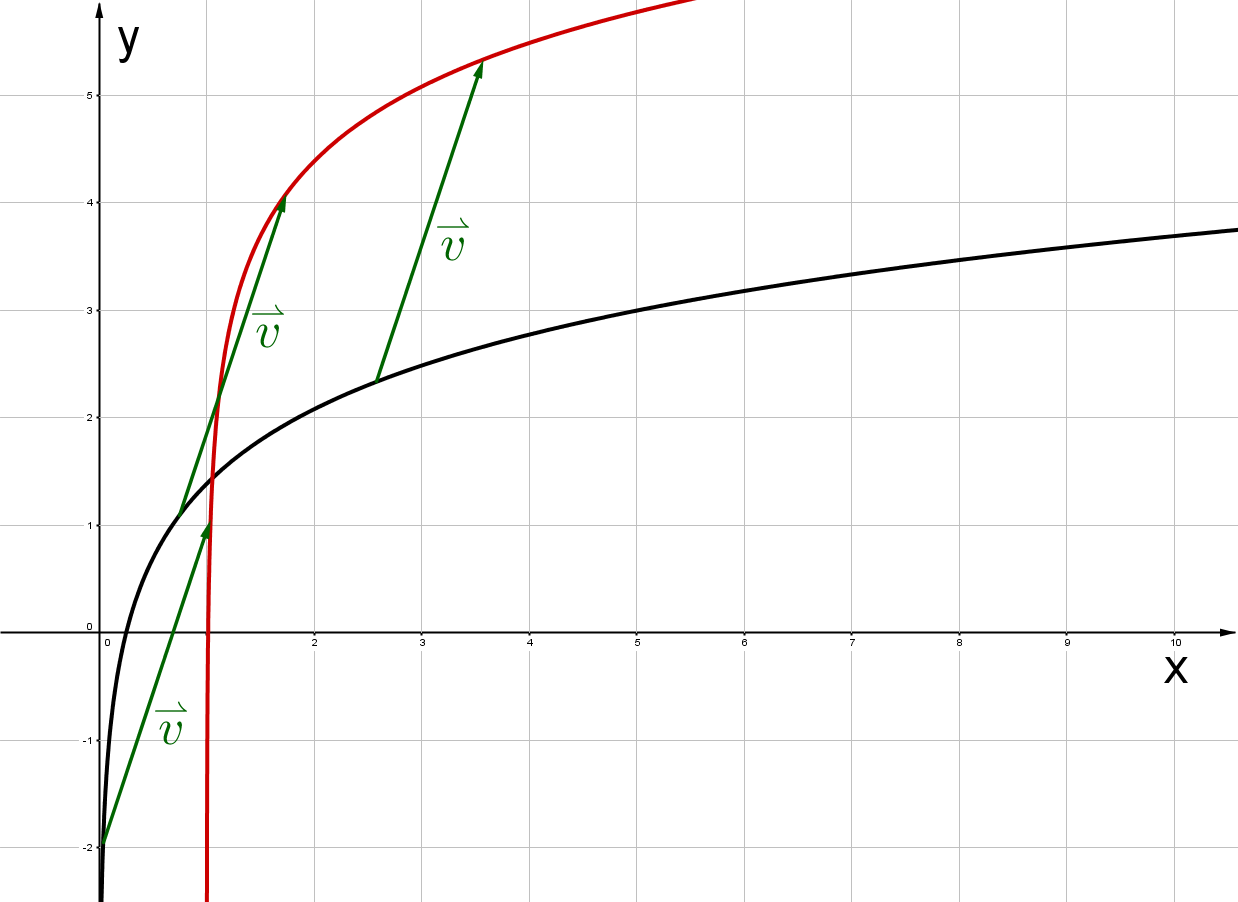
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funktion eine Parallelverschiebung um den Vektor durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
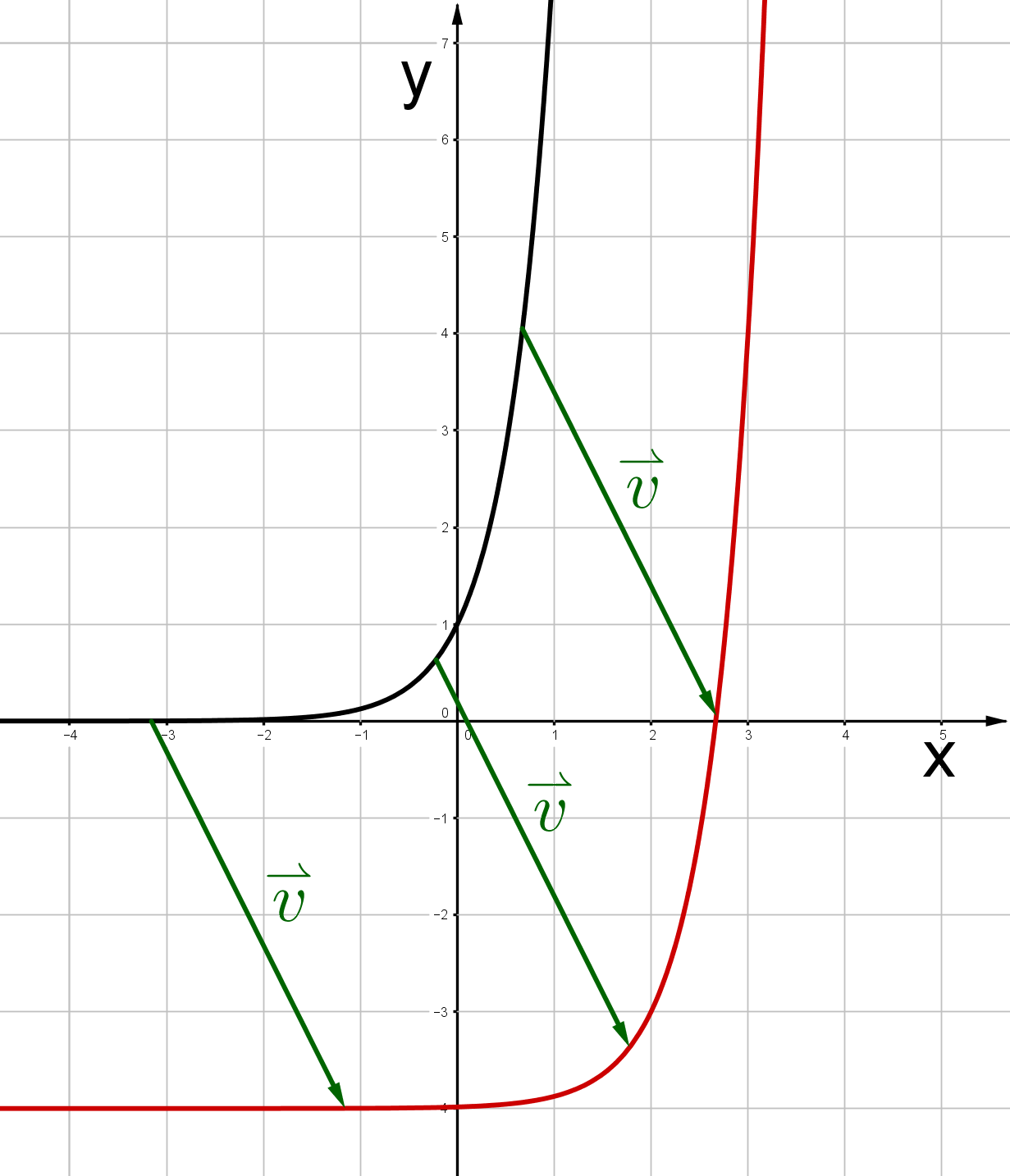
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funktion eine Parallelverschiebung um den Vektor durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?