Die Graphen der Sinus- und Kosinusfunktion können auf verschiedene Weise verändert werden. Sie können in - und -Richtung verschoben, gestreckt oder gestaucht sein.
Eine veränderte trigonometrische Funktion kann zum Beispiel so aussehen:
Um die Veränderungen leichter beschreiben zu können, klammert man den Faktor vor dem aus:
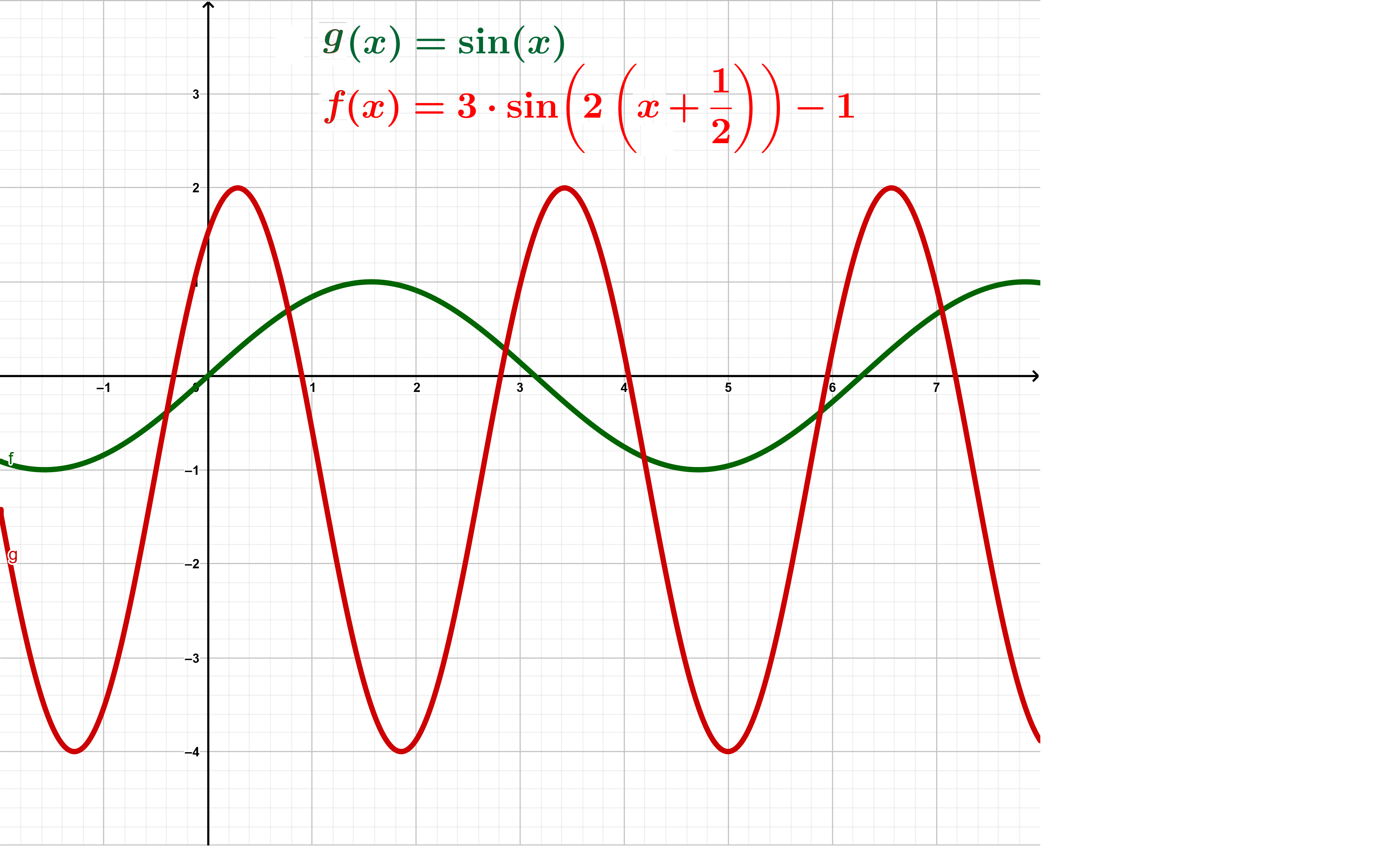
Graphen von und
Allgemeine Form
Sinus:
Kosinus:
Die reellen Parameter bestimmen, wie der Graph genau verändert wird.
Bemerkung: Nicht nur trigonometrische Funktionen lassen sich so verändern. Unter den folgenden Links findest du, wie man den Graphen einer beliebigen Funktion verschiebt oder staucht, oder streckt.
Einfluss der Parameter auf den Funktionsgraphen
Beobachtung an Beispielen
1. Betrachte
Im Applet sieht man, dass sich der Funktionsgraph unter dem Einfluss der Parameter und verändert:
Zunächst wird vom Startwert beginnend bis zum Endwert verändert. Währenddessen verschiebt sich der Funktionsgraph um in -Richtung nach oben. Beim Endwert hat die Funktion die Ruhelage . verändert also die Ruhelage der Funktion.
Danach wird vom Startwert beginnend bis zum Endwert verändert. Währenddessen staucht sich der Funktionsgraph in -Richtung zusammen; die Wellenberge und Wellentäler rücken enger aneinander, die Periode der Funktion wird kleiner. Beim Endwert ist die Periode nur noch statt . verändert also die Periode der Funktion.
2. Betrachte
Auch an diesem Applet sieht man, dass sich der Funktionsgraph unter dem Einfluss der Parameter und verändert:
Zuerst wird vom Startwert beginnend auf den Wert verändert. Dabei verschiebt sich der Funktionsgraph in -Richtung um den Wert nach rechts. verändert also die Lage des Funktionsgraphen in -Richtung.
Danach wird vom Startwert beginnend bis zum Endwert verändert. Dabei wird der Funktionsgraph in -Richtung gestreckt. verändert also die Amplitude der Funktion.
Überblick über den Einfluss der Parameter
Parameter
Der Parameter beeinflusst die Amplitude. Er streckt/staucht den Graphen in -Richtung.
Der Graph hat die Amplitude
: Der Graph wird zusätzlich an der Ruhelage gespiegelt.
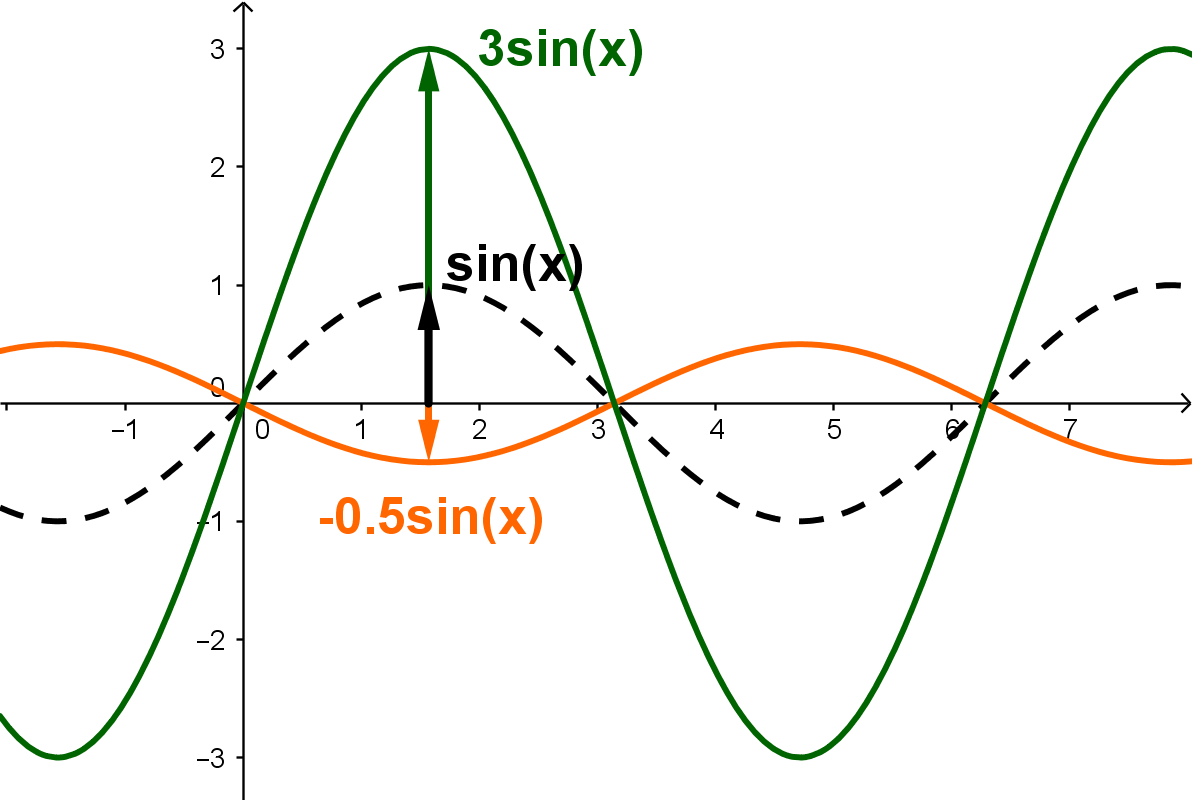
Parameter
Der Parameter beeinflusst die Periode. Er streckt/staucht den Graphen in -Richtung.
Der Graph hat die Periode
: Der Graph wird zusätzlich an der senkrechten Achse gespiegelt
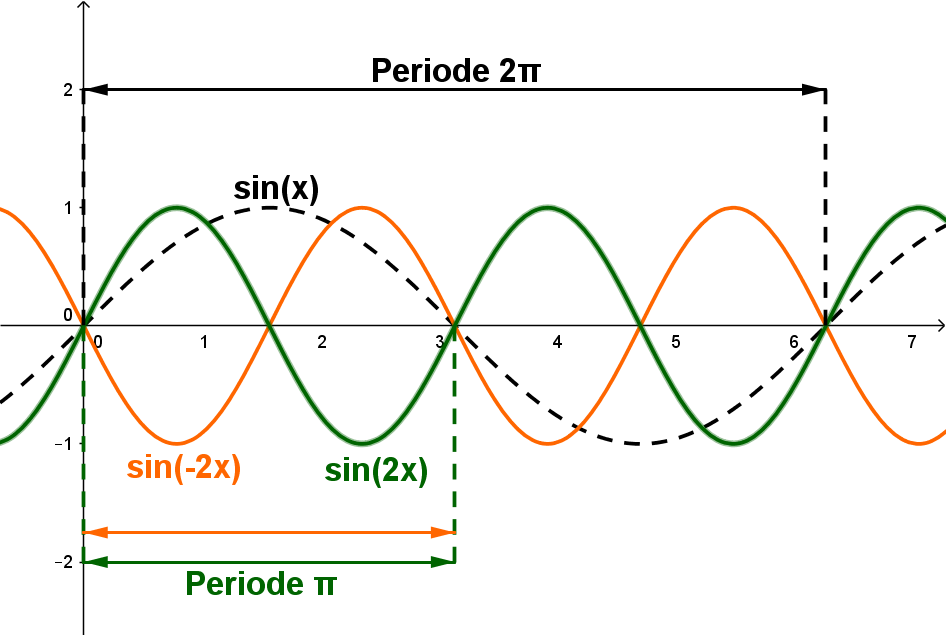
Parameter
Der Parameter verursacht eine Verschiebung in -Richtung
: Verschiebung um nach links
: Verschiebung um nach rechts
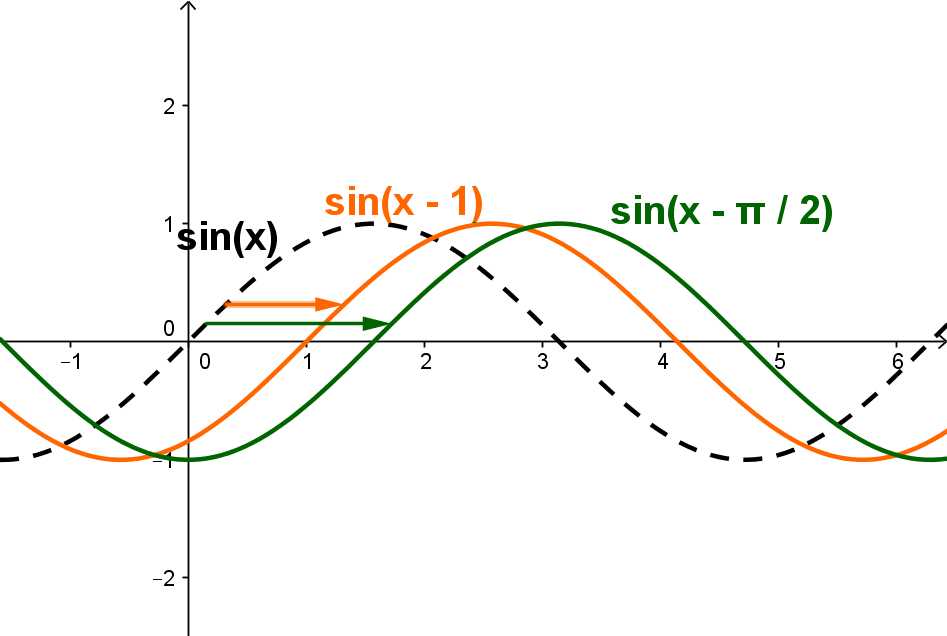
Parameter
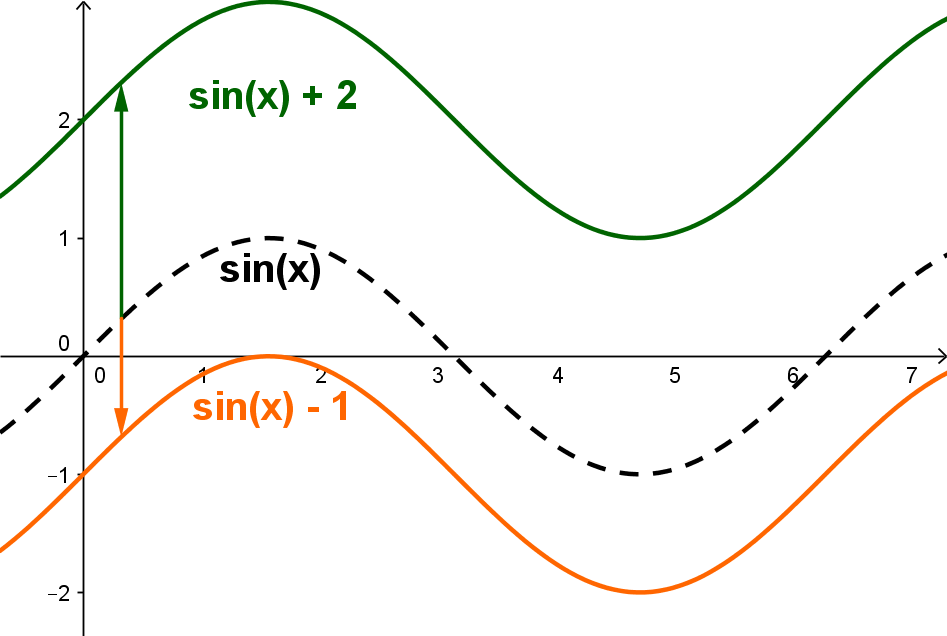
Der Parameter beeinflusst die Ruhelage. Er verschiebt den Graphen in -Richtung
: Verschiebung um nach oben
: Verschiebung um nach unten
Der Graph hat die Ruhelage bei
Zum Ausprobieren im Applet
Die beschriebenen Zusammenhänge sind in folgendem Applet veranschaulicht:
In diesen beiden nachfolgenden Bildern in den Übungsaufgaben siehst du jeweils einen Funktionsgraphen.
Gesucht ist jedes Mal eine Funktionsgleichung, die dazu passt.
Übungsaufgaben
Laden
Laden
Laden
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
