Aufgaben zur Aufstellung von Ebenengleichung
- 1
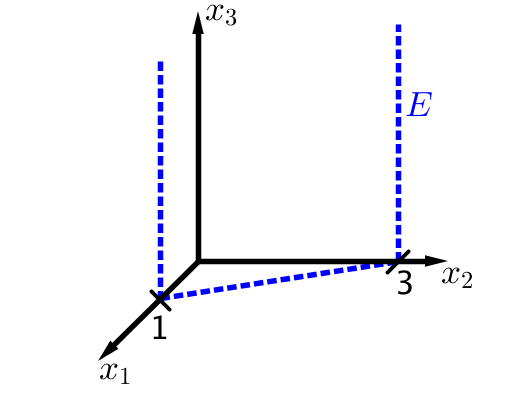
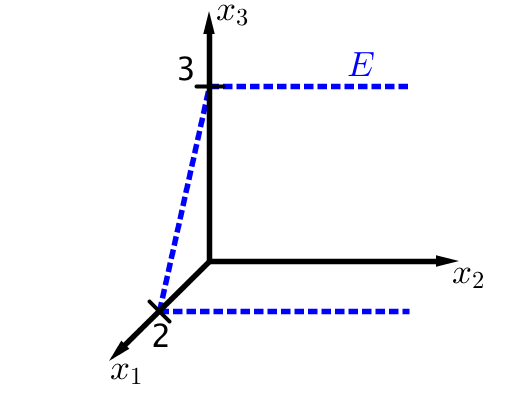
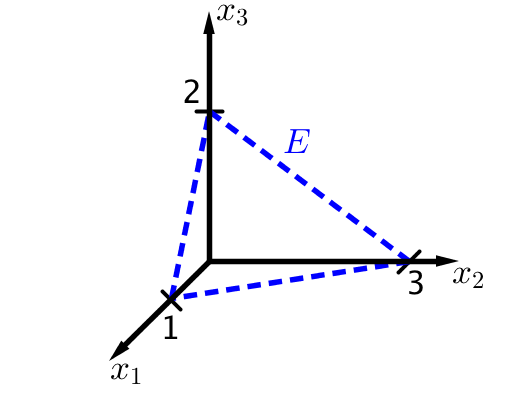
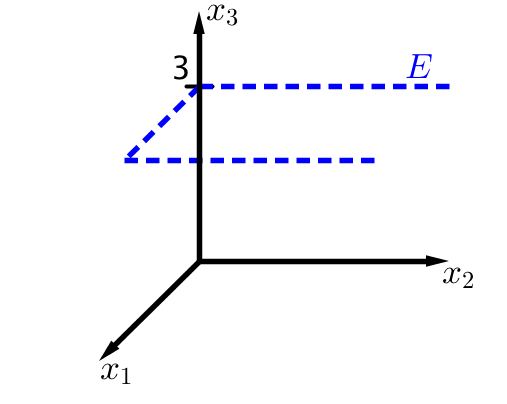
In den folgenden Bildern ist je eine Ebene E dargestellt. Stelle die dargestellte Ebene in Parameterform auf.
- 2
Gegeben sind die parallelen Geraden
und
Bestimme die Gleichung der Ebene in Parameterform, in der die beiden Geraden und liegen.
- 3
Gegeben ist die Gerade und der Punkt , der nicht auf der Geraden liegt.
Bestimme die Gleichung der Ebene in Parameterform, in der der Punkt und die Gerade liegen.
- 4
Gegeben sind die zueinander windschiefen Geraden und . Bestimme die Gleichung der Ebene in Parameterform, in der die Gerade liegt und zu der die Gerade parallel ist.
- 5
Stelle aus den folgenden drei Punkten eine Ebenengleichung in Parameterform auf.
, ,
, ,
, ,
, ,
, ,
, ,
, ,
- 6
Stelle aus zwei Punkten und einem Richtungsvektor eine Ebenengleichung in Parameterform auf.
, ,
, ,
, ,
- 7
Stelle aus einem Punkt und zwei Richtungsvektoren eine Ebenengleichung in Parameterform auf.
, ,
, ,
, ,
- 8
Gegeben sind die Geraden und , die sich im Punkt schneiden. Bestimme die Ebene in Parameterform, in der beide Geraden liegen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?