Stochastik, Teil A, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
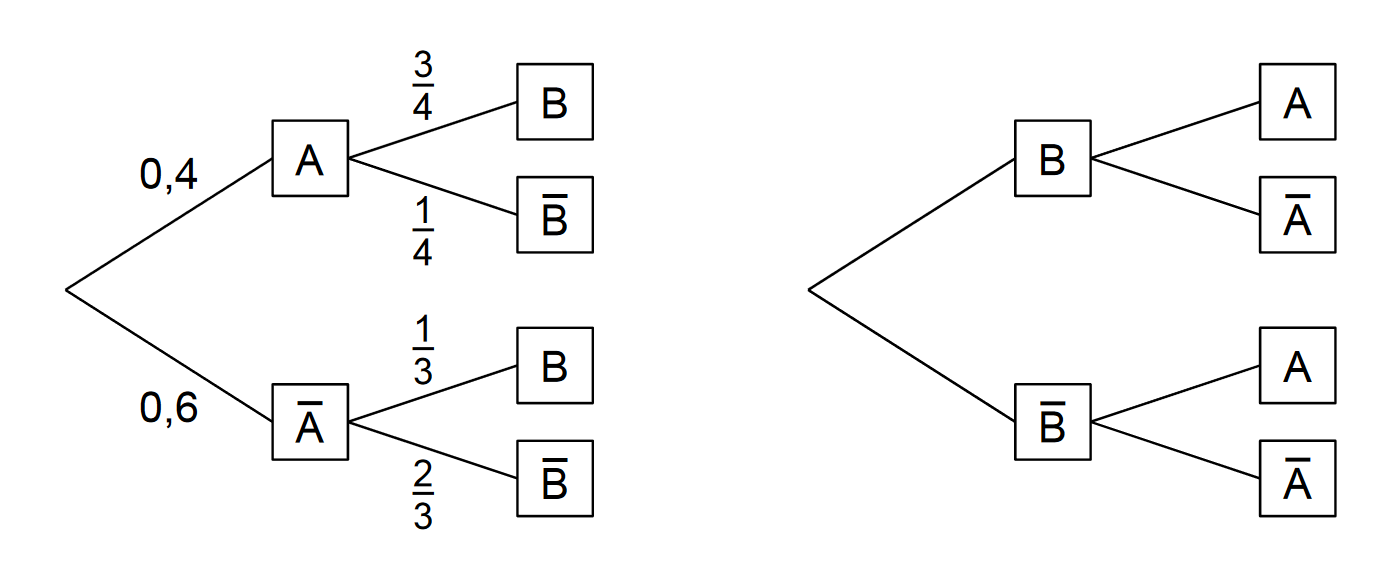
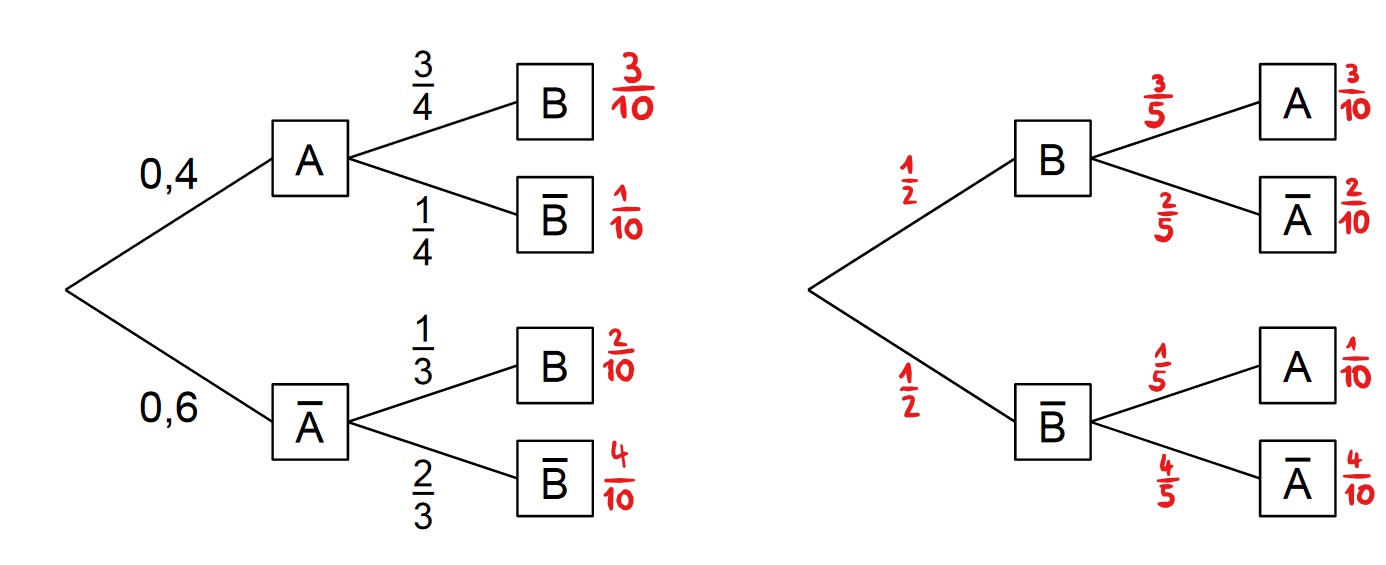
Die beiden Baumdiagramme gehören zum selben Zufallsexperiment mit den Ereignissen und .
Berechnen Sie die Wahrscheinlichkeit und ergänzen Sie anschließend an allen Ästen des rechten Baumdiagramms die zugehörigen Wahrscheinlichkeiten. (Teilergebnis: )
(5 BE)
- 2
Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl oder zum zweiten Mal Wappen oben liegt. Als Ergebnismenge wird festgelegt:
Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist. (2 BE)
Die Zufallsgröße ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von . (3 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?